هندسه شاخه ای از ریاضیات که جبر و حساب در آن کاربرد دارد . هندسه به دو نوع مسطحه و فضایی تقسیم بندی می شود . اگر به جای جبر و حساب از جبر برداری و مختصات دکارتی در آن استفاده شود به آن هندسه تحلیلی گویند .
هندسه ؛ کلیدواژه ی هندسه با ریخت هِندیسه به معنی اَندیزْ نمودن و دیز نمودن و دیزاین نمودن به معنی علم به هم رساندن و به هم جور کردن چیزها می باشد.
روند تغییر ریخت کلمه ی هندسه به صورت هِندیسه قابل تبدیل به کلمه ی اندیشه می باشد.
... [مشاهده متن کامل]
منشعب از کلماتی مثل اندازه ، اندیشه ، اندوختن که دارای ریشه ی ثلاثی ( ن د ز ) می باشد.
بن واژه ی ریشه ثلاثی کلمه ی اندازه دو حرف ( د ز ) می باشد.
ریشه ی کلمه ی هندسه دو حرف ( د س ) می باشد
کلمه ی دِسه با ریخت دِزه به معنی دوز شدن و دیز شدن چیزها و رسیدن آنها به همدیگر با عمل دیزاین نمودن می باشد.
اندازه ؛ با توجه به وجود حرف مصوت تعالی بخش ( آ ) با ذات آوایی تعالی گونه ای که ایجاد می کند در میان ساختمان کلمه ی اندازه مرتبط با کلمه ی دوز شدن و دیزاین به معنی مقدار و میزان فاصله ها یا مقدار جدا بودن یا مقدار لقّی.
ولی در کلمه ی دوز و دیز و دیزاین علم مقدار به هم رسیدن و مرتبط شدن و متصل شدن و جور کردن چیزها به همدیگر با توجه به وجود مصوت حرف ( ی ) در میان ساختمان این کلمه می باشد.
دوز ؛ دوخته شدن ، به هم دیز شدن مثل دوز شدن مهره ها در بازی دوز دوز
در قانون مُصَوِّت ها دو کلمه ی داز و دیز دو مفهوم از هم باز بودن و به هم وصل بودن و به هم رسیدن یا زیاد و کم بودن فاصله معنی می دهد.
مثل دو کلمه ی قال و قیل که مفهوم کلمه ی قال اشاره به مقدار زیاد صدا و کلمه ی قیل اشاره به مقدار کم صدا دارد.
عینیت و انطباق کلمه ی قال با مدل صدور آوای این کلمه به گونه ای است که هنگام صدور آوا دهان همانند یک شیپور صدا به تعالی می رساند ولی در مورد کلمه ی قیل مدل صدور آوا به صورت طبیعی به گونه ای است که صدا دارای قدرت و شدت کمتری از صوت می باشد.
در واقع قانون مصوت ها در کلمات زیادی در ابعاد کاربردی مختلف قابل مشاهده و اعمال شدن است
مثل کلمه ی زیک و زاک یا قیل و قال یا زیپ زاپ یا بیر بار یا بارود با ریخت باروت و برید یا داز و دیز و. . .
بر همین مبنا تفاوت دو کلمه ی اندازه و اندیشه در مورد کلمه ی اندازه اشاره به مقدار پراکنده بودن و جدا بودن و در مورد کلمه ی اندیشه اشاره به مقدار مجتمع بودن و جور شدن چیزها و به هم مرتبط کردن مفاهیم مفهوم می رساند.
یعنی کلمه ی اندیشه با معنی تفکر در واقع علم مرتبط کردن و به هم رساندن مفاهیم به یکدیگر می باشد .
فلسفه ی کلمه ی اندیشیدن این مفهوم را به ما می رساند که اندیشیدن منجر به اندوختن می شود.
پس با این تفاسیر مفهوم کلمه ی هندسه به معنی علم به هم جور نمودن چیزها می باشد و مفهوم کلمه ی اندازه علم مقدار فاصله ها می باشد.
و مفهوم کلمه ی اندیشه به معنی تفکر جهت اندوختن می باشد.
چنانچه بخواهیم روند جریان سیال مفاهیم مشترک در آبراه حروف برای ایجاد کلمات با ریشه ی کلمه ی اندازه و اندیشه را دنبال کنیم به کلمات بسیار زیادی خواهیم رسید که مفهوم جور شدن و مقدار فاصله و فصل و وصل چیزها به همدیگر در همه ی این کلمات وجود دارد مثل ؛
( دست دوست داس دسیسه دَیّوس دیزی دوز دِز دِژ دزد و. . . )
داس ؛ فلسفه ی وجودی کلمه ی داس جهت نامگذاری برای این ابزار دروگری بر مبنای جدا نمودن ساقه از ریشه می باشد
همچنین فلسفه ی کلمه ی دسیسه و دیاثت به عنوان یک عمل زشت از جهت تفرقه افکنی و جدایی اندازی بین افراد می باشد.
اما در مورد کلمه ی دیز در ساختمان کلمه ی دیزاین بر مبنای به هم رساندن و جور نمودن چیزها به یکدیگر می باشد.
منبع. عکس فرهنگ ریشه واژگان فارسی دکتر علی نورایی
زبان های ترکی�در چند مرحله بر�زبان فارسی�تأثیر گذاشته است. نخستین تأثیر زبان ترکی بر پارسی، در زمان حضور سربازان تُرک در ارتش�سامانیان�روی داد. پس از آن، در زمان فرمان روایی�غزنویان، �سلجوقیان�و پس از�حملهٔ مغول، تعداد بیشتری�وام واژهٔ�ترکی به زبان فارسی راه یافت؛ اما بیشترین راه یابی واژه های ترکی به زبان فارسی در زمان فرمانروایی�صفویان، که ترکمانان�قزلباش�در تأسیس آن نقش اساسی داشتند، و�قاجاریان�بر ایران بود.
... [مشاهده متن کامل]
• منابع ها. تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. اول و دوم، انتشارات ققنوس، ۱۳۷۴
• تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. سوم، انتشارات بدیهه، ۱۳۷۴
• حسن بیگ روملو، �احسن التواریخ� ( ۲ جلد ) ، به تصحیح�عبدالحسین نوایی، بنگاه ترجمه و نشر کتاب، ۱۳۴۹. ( مصحح در پایان جلد اول شرح مفصل و سودمندی از فهرست لغات�ترکی�و�مغولی�رایج در متون فارسی از سده هفتم به بعد را نوشته است )
• فرهنگ فارسی، محمد معین، انتشارات امیر کبیر، تهران، ۱۳۷۵
• غلط ننویسیم، ابوالحسن نجفی، مرکز نشر دانشگاهی، تهران، ۱۳۸۶
• فرهنگ کوچک زبان پهلوی، دیوید نیل مکنزی، ترجمه مهشید فخرایی، پژوهشگاه علوم انسانی و مطالعات فرهنگی، تهران، ۱۳۷۹
مشاهده: " تماشا ".
هِنس. هنسه. اندازه=هندسه
هندسه از کلمه اندازه فارسی است و از اصطلاحات دیوان آب در زمان ساسانیان بوده است، اندازه اصطلاحی بوده که در کندن قناتها و تعیین شیب زمین برای جریان افتاده اب بوده است ، و مهندس کسی بوده که مجرای قناتها و جاهایی را که باید قناتها کنده شوند را اندازه گیری میکرده،
... [مشاهده متن کامل]
هندسه همچنین مشتق از کلمه هندزه فارسی است که حرف ز. به سین تبدیل شده است ( از کتاب تاریخ و فرهنگ ایران انتقال از عصر ساسانی به عصر اسلامی، نوشته مرحوم دکتر محمد محمدی ملایری )
خوارزمی در "مفاتیح العلوم" و در تعریف هندسه می نویسد: "این صناعت را در یونان "جومِطریا" می خوانند و آن، صناعت مساحت کردن است. ولی هندسه کلمه ای است فارسیِ معرب، و فارسی آن اندازه است. "
( منبع: کتاب "معمار و معماری در تاریخ اجتماعی ایران، غلامرضا جمال الدین، ص 38 )
منبع. عکس نامهٔ باستان دکتر میر جلال الدین کزازی
زبان های ترکی�در چند مرحله بر�زبان فارسی�تأثیر گذاشته است. نخستین تأثیر زبان ترکی بر پارسی، در زمان حضور سربازان تُرک در ارتش�سامانیان�روی داد. پس از آن، در زمان فرمان روایی�غزنویان، �سلجوقیان�و پس از�حملهٔ مغول، تعداد بیشتری�وام واژهٔ�ترکی به زبان فارسی راه یافت؛ اما بیشترین راه یابی واژه های ترکی به زبان فارسی در زمان فرمانروایی�صفویان، که ترکمانان�قزلباش�در تأسیس آن نقش اساسی داشتند، و�قاجاریان�بر ایران بود.
... [مشاهده متن کامل]
• منابع ها. تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. اول و دوم، انتشارات ققنوس، ۱۳۷۴
• تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. سوم، انتشارات بدیهه، ۱۳۷۴
• حسن بیگ روملو، �احسن التواریخ� ( ۲ جلد ) ، به تصحیح�عبدالحسین نوایی، بنگاه ترجمه و نشر کتاب، ۱۳۴۹. ( مصحح در پایان جلد اول شرح مفصل و سودمندی از فهرست لغات�ترکی�و�مغولی�رایج در متون فارسی از سده هفتم به بعد را نوشته است )
• فرهنگ فارسی، محمد معین، انتشارات امیر کبیر، تهران، ۱۳۷۵
• غلط ننویسیم، ابوالحسن نجفی، مرکز نشر دانشگاهی، تهران، ۱۳۸۶
• فرهنگ کوچک زبان پهلوی، دیوید نیل مکنزی، ترجمه مهشید فخرایی، پژوهشگاه علوم انسانی و مطالعات فرهنگی، تهران، ۱۳۷۹
منبع. عکس فرهنگ پاشنگ
زبان های ترکی�در چند مرحله بر�زبان فارسی�تأثیر گذاشته است. نخستین تأثیر زبان ترکی بر پارسی، در زمان حضور سربازان تُرک در ارتش�سامانیان�روی داد. پس از آن، در زمان فرمان روایی�غزنویان، �سلجوقیان�و پس از�حملهٔ مغول، تعداد بیشتری�وام واژهٔ�ترکی به زبان فارسی راه یافت؛ اما بیشترین راه یابی واژه های ترکی به زبان فارسی در زمان فرمانروایی�صفویان، که ترکمانان�قزلباش�در تأسیس آن نقش اساسی داشتند، و�قاجاریان�بر ایران بود.
... [مشاهده متن کامل]
• منابع ها. تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. اول و دوم، انتشارات ققنوس، ۱۳۷۴
• تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. سوم، انتشارات بدیهه، ۱۳۷۴
• حسن بیگ روملو، �احسن التواریخ� ( ۲ جلد ) ، به تصحیح�عبدالحسین نوایی، بنگاه ترجمه و نشر کتاب، ۱۳۴۹. ( مصحح در پایان جلد اول شرح مفصل و سودمندی از فهرست لغات�ترکی�و�مغولی�رایج در متون فارسی از سده هفتم به بعد را نوشته است )
• فرهنگ فارسی، محمد معین، انتشارات امیر کبیر، تهران، ۱۳۷۵
• غلط ننویسیم، ابوالحسن نجفی، مرکز نشر دانشگاهی، تهران، ۱۳۸۶
• فرهنگ کوچک زبان پهلوی، دیوید نیل مکنزی، ترجمه مهشید فخرایی، پژوهشگاه علوم انسانی و مطالعات فرهنگی، تهران، ۱۳۷۹
.
🔵 واژه مهندس پارسی است
اینکه با دانش اتیمولوژی پارسی بودن واژه � مهندس و هندسه و . . . � را بررسی کنیم، ممکن است برای برخی ها باورپذیر نباشد، ولی وقتی چند زبان شناس عرب زبان در ۱۰۰۰ سال پیش تاکید کرده اند این واژه پارسی است ( تصاویر را ببینید 👇 ) دیگر سخنی برای گفتن باقی نمی ماند :
... [مشاهده متن کامل]
خوارزمی، سده ۴ ق
جـــوهــــری، ســده ۴ ق
اسماعیل بن عباد، سده ۴ق
جـوالـیقـی، ســده ۵ - ۶ قمـری
عـوتبـی صحـاری، سـده ۶ قمـری
♦️ در مفاتیح العلوم خوارزمی سده ۴ قمری چنین گفته شده است :
این صنعت در زبان یونانی "جومطریا" نامیده می شود و به معنای دانش مساحت سنجی است. اما واژه "هندسه" یک کلمه فارسی معرب شده است و در زبان فارسی "اندازه" گفته می شود که به معنای مقادیر است. خلیل می گوید: مهندس کسی است که مسیر قنات ها و محل های حفاری آن ها را تعیین می کند. این کلمه از "هندزه" گرفته شده که واژه ای فارسی است و در هنگام تعریب، حرف "ز" به "س" تبدیل شده است، زیرا در زبان عربی پس از حرف "د"، "ز" نمی آید. برخی گفته اند که "هندسه" از واژه "اندیشه" گرفته شده است، به معنای فکر، اما این نادرست است، زیرا در برخی متون فارسی آمده است: "اندازه با اختر ماری باید"، یعنی هندسه همراه با احکام نجوم مورد نیاز است. همچنین، این نام می تواند به دانش سنجش آب نیز اطلاق شود، همان طور که خلیل گفته است، زیرا این دانش یکی از شاخه های این صنعت محسوب می شود.
.
🔷 واژه هندسه در پارسی از عربی � هندسة � آمده که در عربی نخستین بصورت � هَنْدَزَة �� ( handaza ) بوده و همه اینها، خود از پارسی � اندازه / انداز � و صورت دیگر آن � هندازه / هنداز � آمده اند. ریشه واژه � اندازه / اندازگ � در ایرانی باستان :
از پهلوی ساسانی handāxtan به معنای � طرح کردن، اندیشیدن، حساب کردن، اندازه گرفتن � که این مفهوم، به همان فعل � انداختن � به معنای � پرتاب کردن، انداختن � برمیگردد. چرا و چگونه مفهوم � اندازه گرفتن � به � انداختن � ربط پیدا می کند ؟ زبانشناسان دو نظریه مطرح کرده اند :
☑️ ۱ - نظریه نخست : فعل انداختن از ایرانی باستان ham tāxta آمده ( ماده مضارع آن hamtāča ) و از ریشه tak به معنای تاختن و جاری شدن، و در کل hamtāxta یعنی روان کردن، به حرکت درآوردن چیزی، که همان مفهوم پرتاب کردن و انداختن است. / اندازه گرفتن و حساب کردن نیز یعنی به حرکت درآوردن مغز و برانگیختن ذهن است. / در خود عربی نیز مطرح کردن، از ریشه طرح است که این ریشه به معنای افکندن و انداختن است
☑️ ۲ - نظریه دوم : انداختن و اندازه از همان ریشه hamtāxta به معنای روان کردن، به حرکت درآوردن چیزی، هستند و چون در گذشته با حرکت دادن دست و پا اندازه گیری میکردند ( یعنی پا انداختن، دست انداختن ) این فعل کم کم معنای � اندازه گیری، طرح کردن، نقشه کشیدن و . . . � پیدا کرد. واحدهای اندازه گیری قدیم ایران نیز همگی برمبنای طول دست و پا هستند که با جلو انداختن یکسان دست و پا، اندازه گیری می کردند :
🔺 اَرَش : از پهلوی ساسانی ārešn و از پارسی هخامنشی 𐎠𐎼𐏁𐎴𐎡 ( arašni ) یک واحد اندازه گیری بوده که برابر با فاصله آرنج تا نوک انگشت میانی
🔺 وژه : وجب، بلست، بدست، به فاصله نوک انگشت کوچک تا انگشت بزرگ گفته میشود
🔺 گام : یک واحد اندازه گیری و فاصله میان دو پا هنگام راه رفتن یکنواخت
🔺 جریب : از پهلوی ساسانی و اشکانی griw آمده و یک واحد اندازه گیری سطح ( متر مربع ) برپایه گام یا ارش بوده است
🔺 فرسخ : معرب فرسنگ پارسی و یک واحد اندازه گیری مسافت بوده و تقریبا برابر با ۶. ۲ کیلومتر است ؛ یعنی ۶۰۰۰ � گز � و هر � گز � ( ۱۰۴ س. م ) برابر با ۱۶ گره ( ۶. ۵ س. م ) و هر گره تقریبا یک بند انگشت است.
📘 عطار :
مدرسه با چند مسجد ساختم
خانقه هم چند طرح #انداختم
. . . و�اندیشه�فردا با که�انداختن
📘 فردوسی :
و زان پس یکی چاره ای ساختن
ز هر گونه اندیشه #انداختن
یکی چاره باید کنون ساختن
ز هر گونه اندیشه #انداختن
📘 حافظ :
بیا تا گل برافشانیم و می در ساغر اندازیم
فلک را سقف بشکافیم و #طرحی نو #دراندازیم
نبود نقش دو عالَم، که رنگ الفت بود
زمانه طرح محبّت، نه این زمان #انداخت
📘 جامی :
ز دست خود روانی خنجر�انداخت
به قصد صلح�طرح�دیگر�#انداخت
🆔 @iranzamin777
🆔 Admin @f777kim
. .
🟩 واژه مهندس پارسی است
اینکه با دانش اتیمولوژی پارسی بودن واژه � مهندس و هندسه و . . . � را بررسی کنیم، ممکن است برای برخی ها باورپذیر نباشد، ولی وقتی چند زبان شناس عرب زبان در ۱۰۰۰ سال پیش تاکید کرده اند این واژه پارسی است ( نوشته پیوستی را بخوانید 👆👆 ) دیگر سخنی برای گفتن باقی نمی ماند :
خوارزمی، سده ۴ ق
جـــوهــــری، ســده ۴ ق
اسماعیل بن عباد، سده ۴ق
جـوالـیقـی، ســده ۵ - ۶ قمـری
عـوتبـی صحـاری، سـده ۶ قمـری
🆔 @iranzamin777
🆔 Admin @f777kim
.
الذی یحفظ الکَون من الفوضی ( هرج ومرج ) ویجعل النظم والعدل قائم وکلّ شئ بقدر ویمکن حسابه بالریاضیات والفیزیاء؛ هو المقالید.
لَهُ مَقالیدُ السَّماواتِ وَ الْأَرْضِ وَ الَّذینَ کَفَرُوا بِآیاتِ اللَّهِ أُولئِکَ هُمُ الْخاسِرُونَ63
هندسه: ( عربی شده از پهلوی: هنداچک handācak اندازه ) بخشی از ریاضیات که در باره ی اندازه گیری فضا یا محیط و اشکالی است که می توانند آن فضا را اشغال کنند.
همتای پارسی هندسه واژه ی زیبای پارتی آساگ می باشد.
در اینجا �هندسه� از ریشه �اندازه� گرفته شده است بنابرین اگر بخواهیم این نام را به فارسی در عام شناخته شده تر و سخنور تر بکنیم:
�دانش اندازه گیری�
از وَری دیگر هندسه، دانش آمیختن کشیدن و رایش ( حساب ) کردن است؛ بنابرین میتوان گفت:
... [مشاهده متن کامل]
�نگارایش�
از وَری دیگر هندسه نه عربی است نه کاملا فارسی
به عنوان واژه ای مشترک دو زبانه مشکلی درش نمیبینم
واژه هندسه خود از واژه پارسیِ اندازه یا هندازه از کارواژه انداختن ( هنداختن ) گرفته شده است ولی به گمانِ من، با وجودِ آن، کاربرد آن برای پیکر شناسی ( یا چیزی که امروزه به آن هندسه می گویند چه هندسه اقلیدسی چه هندسه لباچفسکی و چه هندسه ریمانی ) نادرست است، چراکه ما نظریه ای در دانشِ مزداهیک ( ریاضی ) با نام ( Groessenlehre ) یا نگره یِ اندازه ها داریم ( Groesse در زبان آلمانی همان اندازه است که در زبان انگلیسی به آن measure می گویند ) که جدا از هندسه ای است که امروز بدین نام می شناسیم، واژه ( هندسه ) باید به ریختارِ و شکل و ویژگی های آن بپردازد.
... [مشاهده متن کامل]
شاید بپندارید که می توان هندسه را در جای خود نشانید و واژه ( پیمانه ) را به جایِ ( measure یا Groesse ) بکار برد. ولی باید دانست که پیمانه در مزداهی ( ریاضی ) به جای modulus در جستارِ همنهشتیِ نگره یِ عددها کاربرددارد، نیاز به یادآوری است که واژگان modulus ، mode، mood، model همگی با کارواژه یِ پارسیِ ( مودن ) از یک ریشه هستند ( برای نمونه در پی. مودن ) .
پس، از دیدِ من پیمانه و اندازه که برای واژگانِ modulus و measure بکار می روند، درست می باشند ولی برای واژه ( هندسه ) به گمانم باید واژه دیگری برگزید ( همچون پیکرشناسی یا پیکران ) .
فلان چیز هندسی است = فلان چیز پیکرانی است. هندسه = پیکران ( بکارگیریِ واژه یِ ( هَندیسه ) چطور؟؟ ( هَن ( پیشوند ) /دیسه=شکل ) ) از کارواژه هندیسیدن ( اندیسیدن ) .
از همین جا دستِ تک تکِ دوستان را که برای سره سازیِ زبان پاکِ پارسی می کوشند، می فشارم.
چنانکه بسیاری از واژگانِ پیشنهادیِ دوستان ما را در این فتاد یاری نموده است، امیدوارم در اینجا نیز پیشنهادتان رهگشا باشد ویا چنانچه دچار لغزش شده ام، مرا آگاه سازید.
هَندچک ( واژه هندسه تازیکانده " هند چک " است )
Geometry
پیمایش
سنجش
پیکر سنجی ( پیکر. . ، ، شکل )
بی گمان این واژه از هندچک گرفته شده خیلی تابلو هست. انکارش مانند انکار شب و روزه
بعید نیست که این واژه از هندیزه به هندسه تغییر کرده باشد.
این واژه از زبان سانسکریت گرفته شده.
اندازه
واژه ی اندازه ( پارسی ) همان واژه ی �هندسه� به زبان تازی است که هم دانشش و هم واژه اش از ایران به تازیان رسیده و سپس دوباره به شکلی کژ و کوله ( هندسه ) به ما برگردانده شده است.
برگرفته از پانوشت یادداشتی در پیوند زیر:
... [مشاهده متن کامل]
ب. الف. بزرگمهر ششم تیر ماه ۱۳۹۲
https://www. behzadbozorgmehr. com/2013/06/blog - post_9322. html
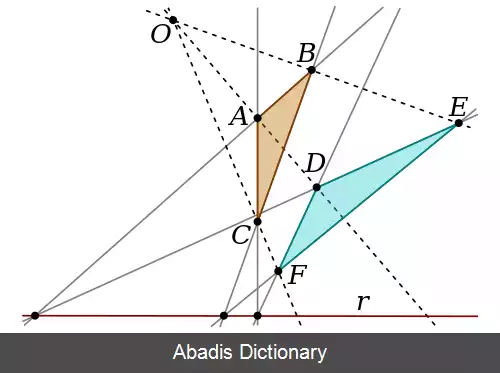
هندسه اقلیدسی و نا اقلیدسی: توضیح می دهد که چطور دو خط موازی در شرایط خاص همدیگر را قطع می کنند.
مستوی تغریف
مخروط تغریف
آخه چطور هندسه از انداختن میاد. واقعا که اصلا هیچ طوری نمی شه ثابت کرد. اصلا معنی نمی ده. بعضی استاد نماها ادبیات فارسی رو خیلی عوض کردن. خوانندگان گرامی حواستون باشه.
هندسه:
دکتر کزازی در مورد واژه ی "هندسه " می نویسد : ( ( هندسه بازخوانده به" هندسه" است و" هندسه" ریخت تاریکانه ی هنداچک handāčag پهلوی است، از مصدر هنداختن handāxtan ( =انداختن ) که در پارسی " اندازه "شده است، از هندسه که در زبان تازی، "چارگانه ی پیراسته" ( = رباعی مجرد ) پنداشته آمده است، "مهندس" و واژگانی دیگر بر آمده اند. ) )
... [مشاهده متن کامل]
( ( به سنگ و به گچ، دیو دیوار کرد؛
نخست ، از بَرَش هندسی کار کرد ؛ ) )
( نامه ی باستان ، جلد اول ، میر جلال الدین کزازی ، 1385، ص 268. )
پس واژه ی " هندسه " همان واژه ی " اندازه ی " فارسی می باشد که پس از سیر در زبان های غیر ایرانی با تغییر لهجه و معنی دوباره به زبان فارسی بازگشته است .
"هندسه"با تلفظ/hendese/ ، معرب هست یعنی در زبان
عربی وجود دارد ؛وبه معنای اندازه ، اندازه گرفتن هست . 🧐
❗برای همین درریاضیات علمی که در مورد اندازه &
اندازه گیری هست هندسه نامیده می شود ؛❗
اندازش، چینِش
هندسه : تازی شده واژه " هندازه ، اندازه" پارسی است که در پهلوی به گونه " هندازگ " آمده و به معنای اندازه گرفتن است و واژه "هندازگر ، اندازه گر " به مهندس در زبان تازی دگرگون شده .
علم کاملی که جهان را فرا گرفته است و ما از ان هیچ چیر نمی دانیم.
انسان در هندسه غرق است متاسفانه از مغروق خود هیچ چیز نمی داند.
من در هندسه مدرن تا کنون 18 جلد کتاب علمی فنی تحقیقی تخصصی منتشر کرده ام.
مشاهده ادامه پیشنهادها (١٠ از ٣١)