پارادوکس برتراند ( به انگلیسی: Bertrand paradox ) یکی از مسائل احتمالاتی است که جوزف برتراند در سال ۱۸۸۹ مطرح کرده است. این مسئله از این قرار است: احتمال اینکه طول وتری تصادفی از یک دایره، بزرگتر از طول ضلع مثلث متساوی الاضلاع محاط در آن دایره باشد، چقدر است؟ شاید در نگاه اول تناقضی به نظر نرسد اما وقتی دقیق شویم متوجه می شویم که در واقع تناقض از آنجا ناشی می شود که چگونه این وتر تصادفی را انتخاب کنیم. استراتژی های مختلفی برای این انتخاب وجود دارند که هر کدام به یک جواب متفاوت می انجامد. در ادامه این استراتژی ها را بررسی می کنیم.
باتوجه به تقارن برای رسم یک وتر تصادفی می توان ابتدا دو نقطهٔ تصادفی روی محیط دایره انتخاب می کنیم و آن ها را به هم وصل می کنیم تا وتر بین این دو نقطه حاصل شود. نقطهٔ اول را A و نقطهٔ دوم را D می نامیم. فرض کنید A یکی از رئوس مثلث متساوی الاضلاع ABC باشد؛ دراینصورت وتر AD وقتی و تنها وقتی بزرگتر از طول ضلع مثلث ABC خواهد بود که نقطهٔ D روی کمان BC قرار بگیرد. از آنجا که طول کمان BC به اندازهٔ ۱/۳ طول محیط دایره است و نقطهٔ D هم به طور تصادفی از محیط دایره انتخاب شده است با احتمال ۱/۳ روی کمان BC قرار می گیرد، لذا احتمال موردنظر نیز برابر ۱/۳ است.
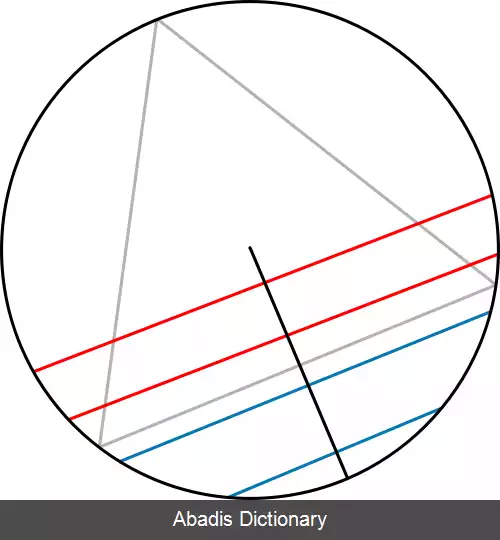
باتوجه به تقارن برای رسم یک وتر تصادفی نقطه ای تصادفی روی محیط دایره انتخاب کرده و آن را به مرکز دایره وصل می کنیم. به این طریق توانسته ایم یک شعاع تصادفی از دایره انتخاب کنیم. سپس نقطه ای تصادفی از روی این شعاع انتخاب می کنیم. وتری وجود دارد که این شعاع در این نقطه عمودمنصف آن است و این وتر وقتی و تنها وقتی از ضلع مثلث متساوی الاضلاع بزرگتر است که نقطه ای که به تصادف روی شعاع انتخاب کرده بودیم، فاصله اش تا مرکز کمتر از نصف شعاع باشد. لذا احتمال مورد نظر در این استراتژی به انتخاب نقطه ای تصادفی روی بازهٔ یکنواخت ( r, 0 ) محدود می شود به طوری که در بازهٔ ( r/2, 0 ) قرار گیرد. پس احتمال موردنظر برابر است با ۱/۲.
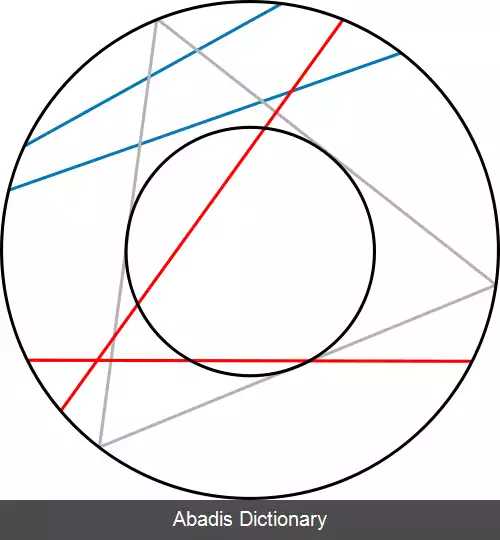
چون هر وتر از دایره عمود بر شعاعی از دایره است که از نقطهٔ وسط آن به مرکز دایره وصل می شود لذا هر وتر به طور یکتا به وسیلهٔ نقطهٔ میانی آن وتر مشخص می شود. برای رسم یک وتر تصادفی نقطه ای تصادفی داخل دایره انتخاب می کنیم و به مرکز دایره وصل می کنیم. سپس وتر عمود بر این خط در نقطهٔ انتخابی را رسم می کنیم. واضح است که این وتر وقتی و تنها وقتی بزرگتر از طول ضلع مثلث متساوی الاضلاع محاط در دایره است که نقطهٔ وسط آن ( یعنی همان نقطهٔ تصادفی که درون دایره انتخاب کردیم ) درون دایره ای قرار بگیرد که هم مرکز با دایره اولیه است و شعاعش نصف شعاع آن است. چون با انتخاب هر نقطه به طور یکتا یک وتر تعیین می شود، لذا احتمال موردنظر برابر است با خارج قسمت مساحت دایرهٔ کوچک به مساحت دایرهٔ اصلی. بنابراین احتمال پیشامد موردنظر برابراست با ۱/۴. همانطور که دیدید سه تعبیر مختلف برای وتر تصادفی منتهی به سه جواب مختلف برای مسئله شد. به این دلیل مسئله برتراند ابتدا به نظر یک پارادوکس می آمد. در آن زمان کسی به این واقعیت دقت نکرد که سه تعبیر مختلف در واقع متناظر با سه آزمایش مختلف برای انتخاب یک وتر تصادفی است. در این فرایند با سه تابع احتمال مختلف که یک مجموعه از پیشامدها تعریف شده اند مواجه بوده ایم.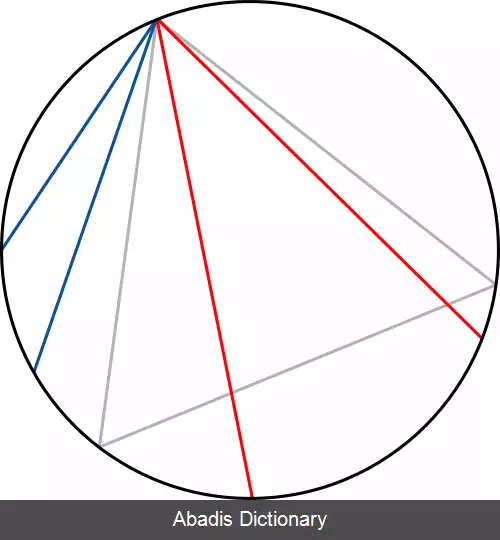

باتوجه به تقارن برای رسم یک وتر تصادفی می توان ابتدا دو نقطهٔ تصادفی روی محیط دایره انتخاب می کنیم و آن ها را به هم وصل می کنیم تا وتر بین این دو نقطه حاصل شود. نقطهٔ اول را A و نقطهٔ دوم را D می نامیم. فرض کنید A یکی از رئوس مثلث متساوی الاضلاع ABC باشد؛ دراینصورت وتر AD وقتی و تنها وقتی بزرگتر از طول ضلع مثلث ABC خواهد بود که نقطهٔ D روی کمان BC قرار بگیرد. از آنجا که طول کمان BC به اندازهٔ ۱/۳ طول محیط دایره است و نقطهٔ D هم به طور تصادفی از محیط دایره انتخاب شده است با احتمال ۱/۳ روی کمان BC قرار می گیرد، لذا احتمال موردنظر نیز برابر ۱/۳ است.
باتوجه به تقارن برای رسم یک وتر تصادفی نقطه ای تصادفی روی محیط دایره انتخاب کرده و آن را به مرکز دایره وصل می کنیم. به این طریق توانسته ایم یک شعاع تصادفی از دایره انتخاب کنیم. سپس نقطه ای تصادفی از روی این شعاع انتخاب می کنیم. وتری وجود دارد که این شعاع در این نقطه عمودمنصف آن است و این وتر وقتی و تنها وقتی از ضلع مثلث متساوی الاضلاع بزرگتر است که نقطه ای که به تصادف روی شعاع انتخاب کرده بودیم، فاصله اش تا مرکز کمتر از نصف شعاع باشد. لذا احتمال مورد نظر در این استراتژی به انتخاب نقطه ای تصادفی روی بازهٔ یکنواخت ( r, 0 ) محدود می شود به طوری که در بازهٔ ( r/2, 0 ) قرار گیرد. پس احتمال موردنظر برابر است با ۱/۲.
چون هر وتر از دایره عمود بر شعاعی از دایره است که از نقطهٔ وسط آن به مرکز دایره وصل می شود لذا هر وتر به طور یکتا به وسیلهٔ نقطهٔ میانی آن وتر مشخص می شود. برای رسم یک وتر تصادفی نقطه ای تصادفی داخل دایره انتخاب می کنیم و به مرکز دایره وصل می کنیم. سپس وتر عمود بر این خط در نقطهٔ انتخابی را رسم می کنیم. واضح است که این وتر وقتی و تنها وقتی بزرگتر از طول ضلع مثلث متساوی الاضلاع محاط در دایره است که نقطهٔ وسط آن ( یعنی همان نقطهٔ تصادفی که درون دایره انتخاب کردیم ) درون دایره ای قرار بگیرد که هم مرکز با دایره اولیه است و شعاعش نصف شعاع آن است. چون با انتخاب هر نقطه به طور یکتا یک وتر تعیین می شود، لذا احتمال موردنظر برابر است با خارج قسمت مساحت دایرهٔ کوچک به مساحت دایرهٔ اصلی. بنابراین احتمال پیشامد موردنظر برابراست با ۱/۴. همانطور که دیدید سه تعبیر مختلف برای وتر تصادفی منتهی به سه جواب مختلف برای مسئله شد. به این دلیل مسئله برتراند ابتدا به نظر یک پارادوکس می آمد. در آن زمان کسی به این واقعیت دقت نکرد که سه تعبیر مختلف در واقع متناظر با سه آزمایش مختلف برای انتخاب یک وتر تصادفی است. در این فرایند با سه تابع احتمال مختلف که یک مجموعه از پیشامدها تعریف شده اند مواجه بوده ایم.




wiki: پارادوکس برتراند
پارادوکس برتراند (اقتصاد). در اقتصاد و تجارت، پارادوکس برتراند - که به نام خالق آن، جوزف برتراند[ ۱] توصیف می شود - وضعیتی را نشان می دهد که در آن دو بازیکن ( شرکت ) به حالت تعادل نش می رسند، جایی که هر دو شرکت هزینه ای برابر با هزینهٔ نهایی درخواست می کنند ( و در نتیجه به سود صفر می رسند ) .
فرض کنید دو شرکت، ۱ و ۲، یک کالای مشابه، هر یک با هزینه های نهایی و توزیع یکسان را به فروش می رسانند، به طوری که مشتریان محصول را تنها بر اساس قیمت انتخاب می کنند. شرکت ارائه دهندهٔ محصول با قیمت کمتر، کل بازار را به دست آورده و اگر قیمت را یکسان تعیین کنند، شرکت ها، بازار و سود را به اشتراک خواهند گذاشت. به این نتیجه رسیده می شود که تقاضا به طور بی کران کشش قیمتی تقاضا دارد. نه ۱ و نه ۲ قیمت بالاتری را نسبت به رقیب تعیین نمی کنند؛ زیرا این کار باعث می شود که کل بازار به رقیبشان برسد. پارادوکس این است که در مدل هایی مانند رقابت کورنو، افزایش تعداد شرکت ها با همگرایی قیمت ها به هزینه نهایی ( و در واقع رسیدن به سود صفر ) پیوند خورده است.
پارادوکس برتراند به ندرت در عمل ظاهر می شود، زیرا محصولات واقعی تقریباً همیشه در ویژگی ای به جز قیمت متفاوت هستند ( حداقل نام تجاری ) ؛ شرکت ها محدودیت هایی در ظرفیت تولید و پخش کردن محصولاتشان دارند؛ و دو شرکت به ندرت هزینه های یکسانی دارند. همچنین موارد دیگر در ادامه آورده شده است. [ ۲]
پارادوکس برتراند اولین بار توسط ریاضی دان فرانسوی، جوزف برتراند، در سال ۱۸۸۳، پس از مدل کورنو در مورد نظریهٔ انحصار چندجانبه و بر مبنای ساخت وکار ارزان ترفروشی به عنوان جایگزین رقابت کمیتی مطرح شد. [ ۳] به طور خلاصه، شرکت ها در مدل رقابت کورنو دریافت کنندهٔ سود هستند. آن ها با پیش بینی رفتار شرکت های دیگر خروجی ای را انتخاب می کنند که سود خودشان را بیشنه کند.
پارادوکس برتراند با این فرض مطرح می شود که تنها دو شرکت در بازار وجود داشته، محصولات آن ها هم سان بوده و هر یک از شرکت ها توانایی تولید محصول برای تمام تقاضاها را دارا می باشد. همچنین نمودار هزینهٔ آن ها یکسان و خطی ( نسبت به تعداد محصولات تولیدی ) می باشد. در این بازی هر یک از قیمت خود را یک مرتبطه به طور هم زمان و مستقل انتخاب می کنند. دو شرکت در مورد قوانین اطلاعات کامل داشته و منطقی می باشند ( هر یک به دنبال بیشینه کردن سود خود است ) . با توجه به شرایط گفته شده، مشتریان ( که فرض می شود منطقی هستند ) همواره محصول ارزان تر را برای خرید انتخاب کرده و در صورت هم قیمت بودن محصولات میزان خرید بین دو شرکت به طور برابر تقسیم می شود.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید دو شرکت، ۱ و ۲، یک کالای مشابه، هر یک با هزینه های نهایی و توزیع یکسان را به فروش می رسانند، به طوری که مشتریان محصول را تنها بر اساس قیمت انتخاب می کنند. شرکت ارائه دهندهٔ محصول با قیمت کمتر، کل بازار را به دست آورده و اگر قیمت را یکسان تعیین کنند، شرکت ها، بازار و سود را به اشتراک خواهند گذاشت. به این نتیجه رسیده می شود که تقاضا به طور بی کران کشش قیمتی تقاضا دارد. نه ۱ و نه ۲ قیمت بالاتری را نسبت به رقیب تعیین نمی کنند؛ زیرا این کار باعث می شود که کل بازار به رقیبشان برسد. پارادوکس این است که در مدل هایی مانند رقابت کورنو، افزایش تعداد شرکت ها با همگرایی قیمت ها به هزینه نهایی ( و در واقع رسیدن به سود صفر ) پیوند خورده است.
پارادوکس برتراند به ندرت در عمل ظاهر می شود، زیرا محصولات واقعی تقریباً همیشه در ویژگی ای به جز قیمت متفاوت هستند ( حداقل نام تجاری ) ؛ شرکت ها محدودیت هایی در ظرفیت تولید و پخش کردن محصولاتشان دارند؛ و دو شرکت به ندرت هزینه های یکسانی دارند. همچنین موارد دیگر در ادامه آورده شده است. [ ۲]
پارادوکس برتراند اولین بار توسط ریاضی دان فرانسوی، جوزف برتراند، در سال ۱۸۸۳، پس از مدل کورنو در مورد نظریهٔ انحصار چندجانبه و بر مبنای ساخت وکار ارزان ترفروشی به عنوان جایگزین رقابت کمیتی مطرح شد. [ ۳] به طور خلاصه، شرکت ها در مدل رقابت کورنو دریافت کنندهٔ سود هستند. آن ها با پیش بینی رفتار شرکت های دیگر خروجی ای را انتخاب می کنند که سود خودشان را بیشنه کند.
پارادوکس برتراند با این فرض مطرح می شود که تنها دو شرکت در بازار وجود داشته، محصولات آن ها هم سان بوده و هر یک از شرکت ها توانایی تولید محصول برای تمام تقاضاها را دارا می باشد. همچنین نمودار هزینهٔ آن ها یکسان و خطی ( نسبت به تعداد محصولات تولیدی ) می باشد. در این بازی هر یک از قیمت خود را یک مرتبطه به طور هم زمان و مستقل انتخاب می کنند. دو شرکت در مورد قوانین اطلاعات کامل داشته و منطقی می باشند ( هر یک به دنبال بیشینه کردن سود خود است ) . با توجه به شرایط گفته شده، مشتریان ( که فرض می شود منطقی هستند ) همواره محصول ارزان تر را برای خرید انتخاب کرده و در صورت هم قیمت بودن محصولات میزان خرید بین دو شرکت به طور برابر تقسیم می شود.

