منیفلد (هندسه). خمینه یا منیفلد ( انگلیسی: Manifold ) ؛ فضای توپولوژی است که در هر نقطه به صورت موضعی شبیه فضای اقلیدسی است. به طور دقیق تر، هر نقطه از فضای n - بعدی دارای همسایگی هومئومورف با فضای اقلیدسی n بعدی است؛ بنابراین اگر بخواهیم دقیق تر بگوییم یک منیفلد بر اساس توصیف فوق یک n - منیفلد است.
یک منیفلد یک بعدی شامل خطوط و دوایر است، اما شکل عدد هشت انگلیسی منیفلد یک بعدی نیست ( چرا که در مرکز عدد هشت انگلیسی دو خم با هم برخورد کرده اند و هیچ همسایگی آن با فضای اقلیدسی یک بعدی هومئومورف نیست ) . منیفلدهای دو بعدی را رویه می نامند. به عنوان مثالی از منیفلدهای دو بعدی می توان به صفحه، کره، چنبره اشاره کرد که تمام آن ها را می توان در فضای سه بعدی نشاند ( بدون این که از خودشان عبور کنند ) اما بطری کلاین و صفحه تصویری حقیقی هم منیفلد دو بعدی هستند که نمی توانند برعکس مثال های قبلی در فضای سه بعدی بنشینند ( immersion ) چون در این صورت الزاماً خودشان را قطع خواهند کرد.
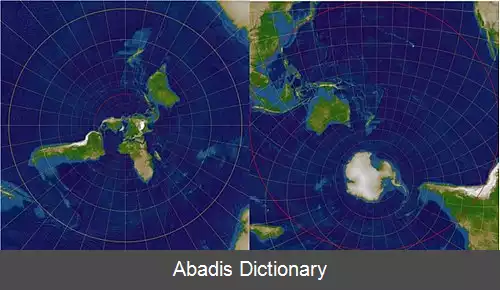
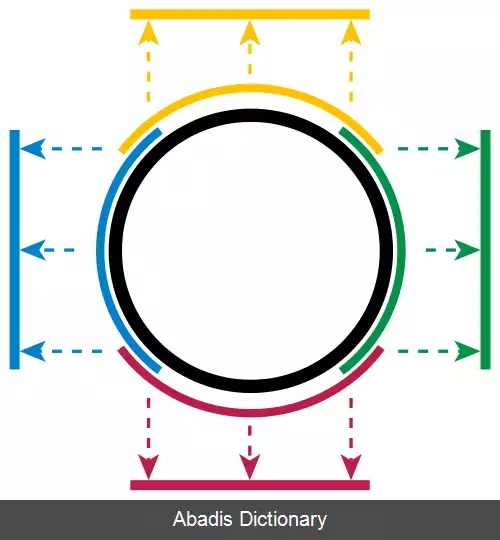
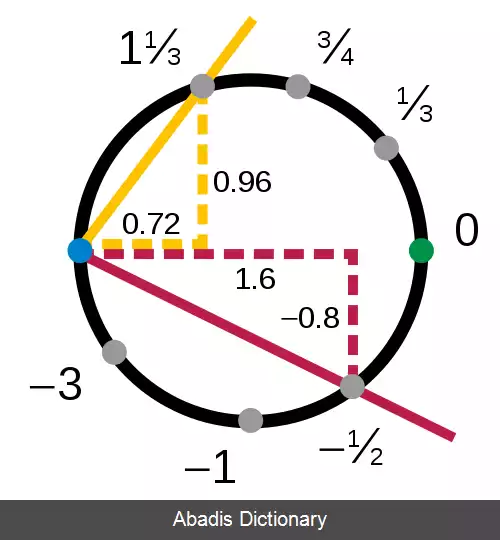
گرچه که یک منیفلد به صورت موضعی شباهت به فضای اقلیدسی دارد، یعنی هر نقطه از آن همسایگی ای دارد که با یک زیرمجموعه باز از فضای اقلیدسی هومئومورف است، اما به طور سراسری ممکن است با فضای اقلیدسی هومئومورف نباشد. به عنوان مثال، رویه کره با صفحه اقلیدسی هومئومورف نیست، چرا که ( علاوه بر خواص دیگر ) خاصیت توپولوژیکی سرتاسری فشردگی را داشته در حالی که فضای اقلیدسی متناظر با آن فشرده نیست، اما در یک ناحیه از کره می توان بوسیلهٔ نگاشت های تصویری چارت هایی ساخت بین آن ناحیه از کره و صفحه دو بعدی اقلیدسی. زمانی که یک ناحیه در دو چارت همسایه پدیدار گردند، آن دو نمایش به طور دقیق با هم یکی نمی شوند و تبدیلی بینشان نیاز است که به آن نگاشت انتقال می گویند.
مفهوم منیفلد در بسیاری از بخش های هندسه و ریاضی - فیزیک مدرن نقش محوری دارد، چرا که امکان توصیف و فهم ساختارهای پیچیده تر را به وسیله خواص توپولوژیکی موضعی ساده تر هندسهٔ اقلیدسی را می دهد. منیفلدها به طور طبیعی در حل مجموعه دستگاه های معادلاتی و نمودار توابع ظاهر می شوند.
منیفلدها را می توان با ساختارهای اضافی مجهز کرد. یک دسته منیفلدهای مهم، منیفلدهای دیفرانسیل پذیر می باشند؛ این ساختار دیفرانسیل پذیر امکان انجام حساب دیفرانسیل و انتگرال را بر روی منیفلدها می دهد. یک متر ریمانی روی منیفلد امکان می دهد تا فواصل و زاویه ها را اندازه گیری کرد. منیفلدهای سیمپلکتیک به عنوان فضای فازی در فرمالیسم همیلتونی مکانیک کلاسیک عمل می کنند، در حالی که منیفلدهای لورنتزی فضازمان را در نسبیت عام مدل می کنند.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک منیفلد یک بعدی شامل خطوط و دوایر است، اما شکل عدد هشت انگلیسی منیفلد یک بعدی نیست ( چرا که در مرکز عدد هشت انگلیسی دو خم با هم برخورد کرده اند و هیچ همسایگی آن با فضای اقلیدسی یک بعدی هومئومورف نیست ) . منیفلدهای دو بعدی را رویه می نامند. به عنوان مثالی از منیفلدهای دو بعدی می توان به صفحه، کره، چنبره اشاره کرد که تمام آن ها را می توان در فضای سه بعدی نشاند ( بدون این که از خودشان عبور کنند ) اما بطری کلاین و صفحه تصویری حقیقی هم منیفلد دو بعدی هستند که نمی توانند برعکس مثال های قبلی در فضای سه بعدی بنشینند ( immersion ) چون در این صورت الزاماً خودشان را قطع خواهند کرد.
گرچه که یک منیفلد به صورت موضعی شباهت به فضای اقلیدسی دارد، یعنی هر نقطه از آن همسایگی ای دارد که با یک زیرمجموعه باز از فضای اقلیدسی هومئومورف است، اما به طور سراسری ممکن است با فضای اقلیدسی هومئومورف نباشد. به عنوان مثال، رویه کره با صفحه اقلیدسی هومئومورف نیست، چرا که ( علاوه بر خواص دیگر ) خاصیت توپولوژیکی سرتاسری فشردگی را داشته در حالی که فضای اقلیدسی متناظر با آن فشرده نیست، اما در یک ناحیه از کره می توان بوسیلهٔ نگاشت های تصویری چارت هایی ساخت بین آن ناحیه از کره و صفحه دو بعدی اقلیدسی. زمانی که یک ناحیه در دو چارت همسایه پدیدار گردند، آن دو نمایش به طور دقیق با هم یکی نمی شوند و تبدیلی بینشان نیاز است که به آن نگاشت انتقال می گویند.
مفهوم منیفلد در بسیاری از بخش های هندسه و ریاضی - فیزیک مدرن نقش محوری دارد، چرا که امکان توصیف و فهم ساختارهای پیچیده تر را به وسیله خواص توپولوژیکی موضعی ساده تر هندسهٔ اقلیدسی را می دهد. منیفلدها به طور طبیعی در حل مجموعه دستگاه های معادلاتی و نمودار توابع ظاهر می شوند.
منیفلدها را می توان با ساختارهای اضافی مجهز کرد. یک دسته منیفلدهای مهم، منیفلدهای دیفرانسیل پذیر می باشند؛ این ساختار دیفرانسیل پذیر امکان انجام حساب دیفرانسیل و انتگرال را بر روی منیفلدها می دهد. یک متر ریمانی روی منیفلد امکان می دهد تا فواصل و زاویه ها را اندازه گیری کرد. منیفلدهای سیمپلکتیک به عنوان فضای فازی در فرمالیسم همیلتونی مکانیک کلاسیک عمل می کنند، در حالی که منیفلدهای لورنتزی فضازمان را در نسبیت عام مدل می کنند.




wiki: منیفلد (هندسه)
