منحنی بزیه ( انگلیسی: Bézier curve ) ، گونه ای منحنی پارامتری مورد استفاده در گرافیک رایانه ای و صنایع مربوط به آن است. تعمیم های منحنی بزیه به ابعاد بالاتر را سطوح بزیه می گویند که یکی از حالت های خاص آن ها، مثلث بزیه است.
در گرافیک برداری، از منحنی های بزیه برای مدل سازی منحنی های نرمی استفاده می شود که می توانند تا بی نهایت بزرگ و کوچک شوند. از پیوند زدن چند منحنی بزیه ساده یک مسیر ( به انگلیسی: Path ) ( منحنی بزیهٔ پیچیده ) حاصل می شود. مسیرها دارای محدودیت های تصویری گرافیک شطرنجی ( به انگلیسی: Raster ) نیستند و کار با آن ها از نظر شهودی آسان است.
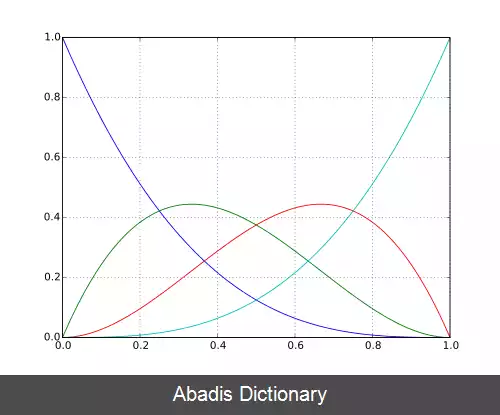
مبنای ریاضیاتی منحنی های بزیه چندجمله ای های برنشتاین است که از سال ۱۹۱۲ شناخته شده بود، ولی از این چندجمله ای تا حدود ۵۰ سال بعد در گرافیک استفاده ای نشد تا این که مهندس فرانسوی پیر بزیه برای طراحی بدنهٔ خودروهای رنو از آن بهره برد.
هر منحنی بزیه دو نقطه لنگر ( به انگلیسی: Anchor point ) و دو نقطه کنترل ( به انگلیسی: Control point ) دارد. نقطه های لنگر ابتدا و انتهای منحنی را مشخص می کنند و نقطه های کنترل انحنای مسیر را تعیین می نمایند. پاره خطی که یک نقطهٔ لنگر را به یک نقطهٔ کنترل وصل می کند، به دستگیره ( به انگلیسی: Handle ) معروف است.
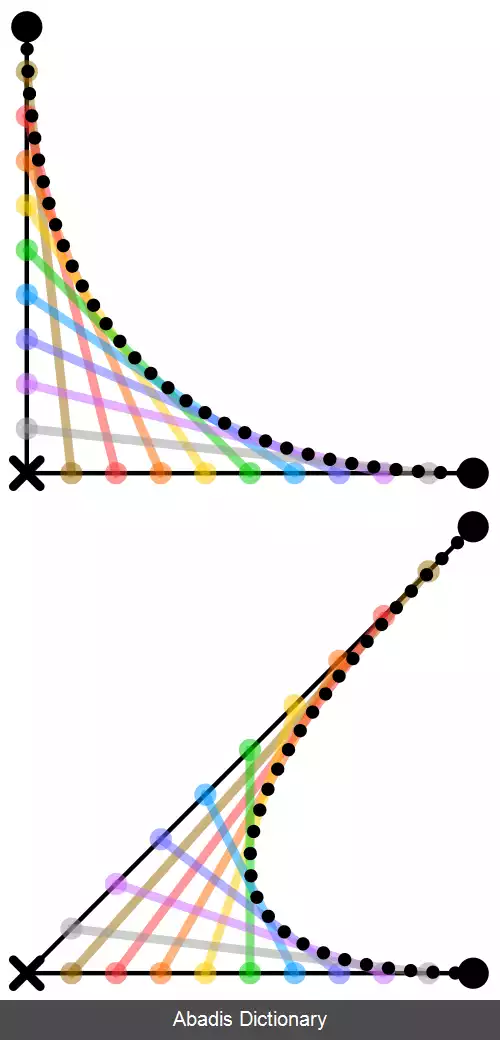
مبنای ریاضی منحنی های بزیه ( چندجمله ای های برنشتاین ) در سال ۱۹۱۲ تبیین شد اما از این چندجمله ای ها در زمینه گرافیک استفاده ای نشد. حدود ۵۰ سال بعد وقتی پل دو کاستلژو ریاضیدان در ۱۹۵۹، الگوریتم دو کاستلژو ( یک روش عددی پایدار برای ارزیابی منحنی ها ) را ایجاد کرد، برای نخستین بار از این چندجمله ای ها در طراحی اتومبیل سیتروئن به کمک رایانه استفاده کرد. [ ۱] این چندجمله ای ها در دهه ۱۹۶۰ توسط مهندس فرانسوی پیر بزیه، که از آن ها برای طراحی بدنه اتومبیل در شرکت رنو استفاده می کرد، به طور گسترده تبلیغ شد.
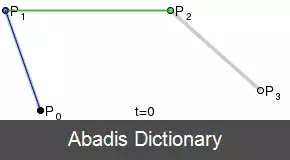
منحنی بزیه توسط مجموعه ای از نقاط کنترل P0 تا Pn تعریف می شود، جایی که n ترتیب آن را می نامند ( n = ۱ برای خطی، ۲ برای درجه دوم و غیره ) . اولین و آخرین نقاط کنترل همیشه نقاط انتهایی منحنی هستند. با این حال، نقاط کنترل میانی ( در صورت وجود ) به طور کلی روی منحنی قرار ندارند. در بخش های زیر، همه ی ترکیب های خطی را آفین در نظر بگیرید؛ یعنی حاصل جمع ضرایب، برابر 1 است.
با توجه به نقاط مجزای P0 و P1، یک منحنی خطی بزیه فقط یک خط مستقیم بین این دو نقطه است. این منحنی را با معادله ی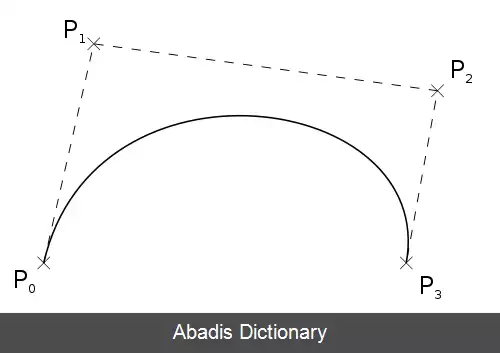
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر گرافیک برداری، از منحنی های بزیه برای مدل سازی منحنی های نرمی استفاده می شود که می توانند تا بی نهایت بزرگ و کوچک شوند. از پیوند زدن چند منحنی بزیه ساده یک مسیر ( به انگلیسی: Path ) ( منحنی بزیهٔ پیچیده ) حاصل می شود. مسیرها دارای محدودیت های تصویری گرافیک شطرنجی ( به انگلیسی: Raster ) نیستند و کار با آن ها از نظر شهودی آسان است.
مبنای ریاضیاتی منحنی های بزیه چندجمله ای های برنشتاین است که از سال ۱۹۱۲ شناخته شده بود، ولی از این چندجمله ای تا حدود ۵۰ سال بعد در گرافیک استفاده ای نشد تا این که مهندس فرانسوی پیر بزیه برای طراحی بدنهٔ خودروهای رنو از آن بهره برد.
هر منحنی بزیه دو نقطه لنگر ( به انگلیسی: Anchor point ) و دو نقطه کنترل ( به انگلیسی: Control point ) دارد. نقطه های لنگر ابتدا و انتهای منحنی را مشخص می کنند و نقطه های کنترل انحنای مسیر را تعیین می نمایند. پاره خطی که یک نقطهٔ لنگر را به یک نقطهٔ کنترل وصل می کند، به دستگیره ( به انگلیسی: Handle ) معروف است.
مبنای ریاضی منحنی های بزیه ( چندجمله ای های برنشتاین ) در سال ۱۹۱۲ تبیین شد اما از این چندجمله ای ها در زمینه گرافیک استفاده ای نشد. حدود ۵۰ سال بعد وقتی پل دو کاستلژو ریاضیدان در ۱۹۵۹، الگوریتم دو کاستلژو ( یک روش عددی پایدار برای ارزیابی منحنی ها ) را ایجاد کرد، برای نخستین بار از این چندجمله ای ها در طراحی اتومبیل سیتروئن به کمک رایانه استفاده کرد. [ ۱] این چندجمله ای ها در دهه ۱۹۶۰ توسط مهندس فرانسوی پیر بزیه، که از آن ها برای طراحی بدنه اتومبیل در شرکت رنو استفاده می کرد، به طور گسترده تبلیغ شد.
منحنی بزیه توسط مجموعه ای از نقاط کنترل P0 تا Pn تعریف می شود، جایی که n ترتیب آن را می نامند ( n = ۱ برای خطی، ۲ برای درجه دوم و غیره ) . اولین و آخرین نقاط کنترل همیشه نقاط انتهایی منحنی هستند. با این حال، نقاط کنترل میانی ( در صورت وجود ) به طور کلی روی منحنی قرار ندارند. در بخش های زیر، همه ی ترکیب های خطی را آفین در نظر بگیرید؛ یعنی حاصل جمع ضرایب، برابر 1 است.
با توجه به نقاط مجزای P0 و P1، یک منحنی خطی بزیه فقط یک خط مستقیم بین این دو نقطه است. این منحنی را با معادله ی






wiki: منحنی بزیه
