قضیهٔ اساسی حساب ( به انگلیسی: Fundamental theorem of arithmetic ) ، از قضایای مهم در نظریۀ اعداد است که نشان می دهد اعداد اول چگونه همانند بلوک های ساختمانی در ساختن سایر اعداد نقش دارند.
این قضیه به طور ساده بیان می کند که هر عدد صحیح به جز 1 و − 1 ، به صورت حاصل ضربی از عوامل اول قابل نمایش است. همچنین این نمایش اعداد به صورت حاصل ضرب عوامل اول، صرف نظر از ترتیب عوامل یکتا است. به عنوان مثال، عدد ۶۰ را می توان به صورت 2 ⋅ 2 ⋅ 3 ⋅ 5 = 60 به حاصل ضرب عوامل اول نوشت. [ ۱]
اگر عدد n را به صورت n = p 1 p 2 p 3 ⋯ p r به حاصل ضرب عوامل اول بنویسم، این کار را اصطلاحاً تجزیه عدد n به عوامل اول می گوئیم. پس قضیهٔ اساسی حساب بیان می کند که هر عدد صحیح به جز 1 و − 1 ، قابل تجزیه به عوامل اول است و این تجزیه صرف نظر از ترتیب عوامل یکتا است. [ ۲]
باید توجه داشت که از نظر تاریخی این قضیه اساساً توسط اقلیدس به اثبات رسیده است، اما اولین اثبات کامل از آن توسط گاوس در کتاب تحقیقات حساب منتشر شده است.
همچنین، با گسترش جبرمجرد و نظریۀ حلقه، مفهومی مشابه در نظریۀ حلقه به عنوان حوزۀ تجزیۀ یکتا ( UFD ) به وجود آمد که در آن ها خاصیتی مشابه برقرار است که توسط کومر و زمانی که بروی قضیه آخر فرما کار می کرد، معرفی شد. این نشان می دهد که اگر چه قضیهٔ اساسی حساب در حلقۀ اعداد صحیح بدیهی جلوه می کند، اما چنین چیزی در مورد هر حلقۀ دلخواه بدیهی نیست و ممکن است نادرست باشد.
برهان قضیه شامل دو قسمت وجود و یکتایی است. ابتدا نشان می دهیم هر عدد را می توان به صورت حاصل ضربی از عوامل اول نوشت. این کار را مبتنی بر اصل استقراء روی n انجام می دهیم.
اگر n = 2 ، چون ۲ خود عددی اول است، پس حکم برقرار است. فرض می کنیم حکم برای هر عدد طبیعی کوچک تر از n = k برقرار باشد. نشان می دهیم که حکم برای n = k نیز برقرار است و بنابر اصل استقراء ریاضی نتیجه می گیریم که حکم برای هر عدد طبیعی ای درست است.
اگر k اول باشد در این صورت چیزی برای اثبات نمی ماند و حکم برقرار است. اگر k اول نباشد در این صورت اعداد صحیح a , b وجود دارند که k = a b و 1 < a ≤ b < k . چون a , b < k ، پس بنابر فرض استقراء a و b به حاصل ضرب عوامل اول تجزیه می شوند. پس a = p 1 p 2 p 3 ⋯ p r و b = q 1 q 2 q 3 ⋯ q s که در آن p i و q j - ها اعداد اول و نه لزوماً متمایز هستند؛ بنابراین k = a b = p 1 p 2 ⋯ p r q 1 q 2 ⋯ q s و لذا k نیز به حاصل ضرب عوامل اول تجزیه می شود.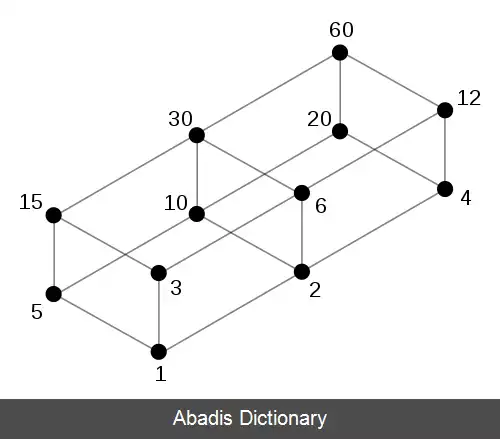
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین قضیه به طور ساده بیان می کند که هر عدد صحیح به جز 1 و − 1 ، به صورت حاصل ضربی از عوامل اول قابل نمایش است. همچنین این نمایش اعداد به صورت حاصل ضرب عوامل اول، صرف نظر از ترتیب عوامل یکتا است. به عنوان مثال، عدد ۶۰ را می توان به صورت 2 ⋅ 2 ⋅ 3 ⋅ 5 = 60 به حاصل ضرب عوامل اول نوشت. [ ۱]
اگر عدد n را به صورت n = p 1 p 2 p 3 ⋯ p r به حاصل ضرب عوامل اول بنویسم، این کار را اصطلاحاً تجزیه عدد n به عوامل اول می گوئیم. پس قضیهٔ اساسی حساب بیان می کند که هر عدد صحیح به جز 1 و − 1 ، قابل تجزیه به عوامل اول است و این تجزیه صرف نظر از ترتیب عوامل یکتا است. [ ۲]
باید توجه داشت که از نظر تاریخی این قضیه اساساً توسط اقلیدس به اثبات رسیده است، اما اولین اثبات کامل از آن توسط گاوس در کتاب تحقیقات حساب منتشر شده است.
همچنین، با گسترش جبرمجرد و نظریۀ حلقه، مفهومی مشابه در نظریۀ حلقه به عنوان حوزۀ تجزیۀ یکتا ( UFD ) به وجود آمد که در آن ها خاصیتی مشابه برقرار است که توسط کومر و زمانی که بروی قضیه آخر فرما کار می کرد، معرفی شد. این نشان می دهد که اگر چه قضیهٔ اساسی حساب در حلقۀ اعداد صحیح بدیهی جلوه می کند، اما چنین چیزی در مورد هر حلقۀ دلخواه بدیهی نیست و ممکن است نادرست باشد.
برهان قضیه شامل دو قسمت وجود و یکتایی است. ابتدا نشان می دهیم هر عدد را می توان به صورت حاصل ضربی از عوامل اول نوشت. این کار را مبتنی بر اصل استقراء روی n انجام می دهیم.
اگر n = 2 ، چون ۲ خود عددی اول است، پس حکم برقرار است. فرض می کنیم حکم برای هر عدد طبیعی کوچک تر از n = k برقرار باشد. نشان می دهیم که حکم برای n = k نیز برقرار است و بنابر اصل استقراء ریاضی نتیجه می گیریم که حکم برای هر عدد طبیعی ای درست است.
اگر k اول باشد در این صورت چیزی برای اثبات نمی ماند و حکم برقرار است. اگر k اول نباشد در این صورت اعداد صحیح a , b وجود دارند که k = a b و 1 < a ≤ b < k . چون a , b < k ، پس بنابر فرض استقراء a و b به حاصل ضرب عوامل اول تجزیه می شوند. پس a = p 1 p 2 p 3 ⋯ p r و b = q 1 q 2 q 3 ⋯ q s که در آن p i و q j - ها اعداد اول و نه لزوماً متمایز هستند؛ بنابراین k = a b = p 1 p 2 ⋯ p r q 1 q 2 ⋯ q s و لذا k نیز به حاصل ضرب عوامل اول تجزیه می شود.

wiki: قضیه اساسی حساب
