در ریاضیات، فرضیه ریمان ( به انگلیسی: Riemann Hypothesis ) ، حدسی است که ادعا می کند صفرهای تابع زتای ریمان فقط در اعداد منفی زوج حقیقی یا اعداد مختلطی با بخش حقیقی 1 2 می باشند. بسیاری این فرضیه را مهم ترین مسئلهٔ حل نشده در ریاضیات محض می دانند. [ ۱] این حدس در نظریه اعداد مورد علاقه و توجه زیادی است، چرا که نتایجی را در مورد توزیع اعداد اول ایجاب می کند. این حدس توسط برنهارت ریمان در ۱۸۵۰ ارائه و به نام خودش نامگذاری شد.
حدس ریمان و برخی از تعمیمات آن، به همراه حدس گلدباخ و حدس اعداد اول دوقلو، مسئله هشتم هیلبرت را در فهرست مسائل ۲۳ گانه حل نشده دیوید هیلبرت تشکیل می دهند؛ همچنین این مسئله یکی از مسائل جایزه هزاره مؤسسه ریاضیاتی کِلِی است. برخی مواقع این عنوان را برای فرض های مشابهی چون فرضیه ریمان برای منحنی های روی میدان های متناهی نیز به کار می برند.
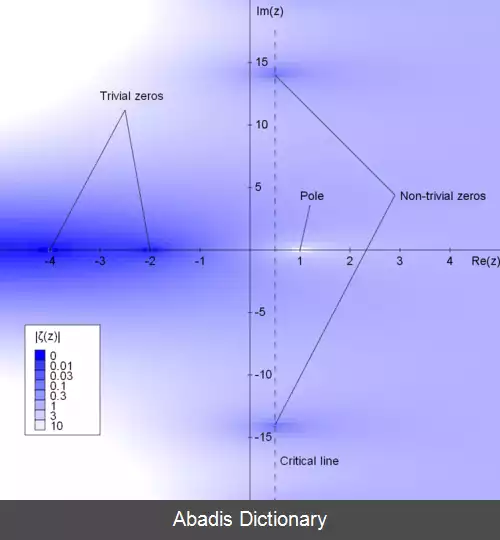
تابع زتای ریمان ζ ( s ) ، تابعی است که آرگومان sش می تواند هر عدد مختلطی به جز ۱ باشد، به گونه ای که مقادیرش نیز مختلط اند. این تابع صفرهایی در اعداد صحیح منفی زوج دارد؛ یعنی اگر s برابر یکی از اعداد: ۲ - ، ۴ - ، ۶ - ، … باشد، ζ ( s ) = 0 خواهد بود. به این صفرها، صفرهای بدیهی تابع زتای ریمان می گویند. با این حال، این ها تنها صفرهای تابع زتای ریمان نیستند، این تابع دارای صفرهای دیگری به نام صفرهای نابدیهی نیز می باشد. فرضیه ریمان مربوط به تعیین مکان صفرهای نابدیهی این تابع بوده و بیان می کند:
بخش حقیقی هر صفر نابدیهی از تابع زتای ریمان 1 2 است.
ازین رو، اگر فرضیه ریمان صحیح باشد، تمام صفرهای نابدیهی تابع مذکور بر روی خط بحرانی شامل اعداد صفحه مختلط به فرم 1 2 + i t خواهند بود، که t عددی حقیقی و i یکه موهومی است.
تابع زتای ریمان برای اعداد مختلط s با مقدار حقیقی بزرگ تر از ۱ با سری بی نهایت همگرای زیر تعریف می شود.
لئونارد اویلر در دهه ۱۷۳۰ این سری را برای اعداد حقیقی بررسی کرده بود و راه حلی هم برای مسئله بازل ارائه کرده بود. او همچنین ثابت کرده بود که مقدار این سری برابر با حاصل ضرب اویلر است.
که در آن حاصل ضرب بینهایت بر روی تمام اعداد اول است.
حدس ریمان در ریشه هایی بحث می کند که خارج از منطقه همگرایی این سری و حاصل ضرب اویلر است. برای این که این حدس معنی پیدا کند، باید به طور تحلیلی این تابع را ادامه داد تا برای همه اعداد مختلط تعریف شود. این کار را می توان با تبدیل جمله های سری با استفاده از تابع اتای دیریکله به صورت زیر انجام داد. اگر مقدار حقیقی s بیشتر از یک است، تابع زتا در معادله زیر صدق می کند.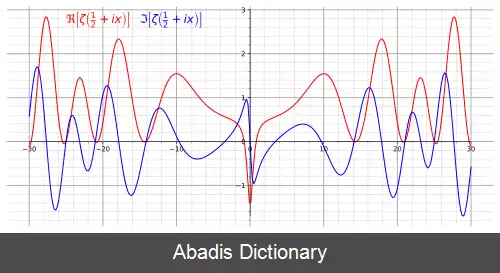
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفحدس ریمان و برخی از تعمیمات آن، به همراه حدس گلدباخ و حدس اعداد اول دوقلو، مسئله هشتم هیلبرت را در فهرست مسائل ۲۳ گانه حل نشده دیوید هیلبرت تشکیل می دهند؛ همچنین این مسئله یکی از مسائل جایزه هزاره مؤسسه ریاضیاتی کِلِی است. برخی مواقع این عنوان را برای فرض های مشابهی چون فرضیه ریمان برای منحنی های روی میدان های متناهی نیز به کار می برند.
تابع زتای ریمان ζ ( s ) ، تابعی است که آرگومان sش می تواند هر عدد مختلطی به جز ۱ باشد، به گونه ای که مقادیرش نیز مختلط اند. این تابع صفرهایی در اعداد صحیح منفی زوج دارد؛ یعنی اگر s برابر یکی از اعداد: ۲ - ، ۴ - ، ۶ - ، … باشد، ζ ( s ) = 0 خواهد بود. به این صفرها، صفرهای بدیهی تابع زتای ریمان می گویند. با این حال، این ها تنها صفرهای تابع زتای ریمان نیستند، این تابع دارای صفرهای دیگری به نام صفرهای نابدیهی نیز می باشد. فرضیه ریمان مربوط به تعیین مکان صفرهای نابدیهی این تابع بوده و بیان می کند:
بخش حقیقی هر صفر نابدیهی از تابع زتای ریمان 1 2 است.
ازین رو، اگر فرضیه ریمان صحیح باشد، تمام صفرهای نابدیهی تابع مذکور بر روی خط بحرانی شامل اعداد صفحه مختلط به فرم 1 2 + i t خواهند بود، که t عددی حقیقی و i یکه موهومی است.
تابع زتای ریمان برای اعداد مختلط s با مقدار حقیقی بزرگ تر از ۱ با سری بی نهایت همگرای زیر تعریف می شود.
لئونارد اویلر در دهه ۱۷۳۰ این سری را برای اعداد حقیقی بررسی کرده بود و راه حلی هم برای مسئله بازل ارائه کرده بود. او همچنین ثابت کرده بود که مقدار این سری برابر با حاصل ضرب اویلر است.
که در آن حاصل ضرب بینهایت بر روی تمام اعداد اول است.
حدس ریمان در ریشه هایی بحث می کند که خارج از منطقه همگرایی این سری و حاصل ضرب اویلر است. برای این که این حدس معنی پیدا کند، باید به طور تحلیلی این تابع را ادامه داد تا برای همه اعداد مختلط تعریف شود. این کار را می توان با تبدیل جمله های سری با استفاده از تابع اتای دیریکله به صورت زیر انجام داد. اگر مقدار حقیقی s بیشتر از یک است، تابع زتا در معادله زیر صدق می کند.


wiki: فرضیه ریمان
