ریشه واحد ( انگلیسی: root of unity ) یا عدد دو مواور در ریاضیات، هر عدد مختلطی است که وقتی به توان عدد صحیح مثبت n برسد حاصل آن ۱ بشود. از ریشه های واحد در بسیاری از رشته های ریاضیات استفاده می شود اما در نظریهٔ اعداد، نظریه کاراکتر گروه، و تبدیل فوریه گسسته نقش مهمتری دارند.
ریشه واحد را در هر میدانی می توان تعریف کرد. اگر مشخصه میدان صفر باشد، ریشه ها اعداد مختلطی هستند که عدد صحیح جبری هم هستند. برای میدان های دارای مشخصه مثبت، ریشه ها به یک میدان متناهی تعلق دارند، و برعکس، هر عنصر غیرصفر از یک میدان متناهی یک ریشه واحد است. هر میدان بسته جبری دقیقا شامل n تا ریشه nام از واحد است، بجز وقتیکه n یک مضرب از مشخصه ( مثبت ) میدان باشد.
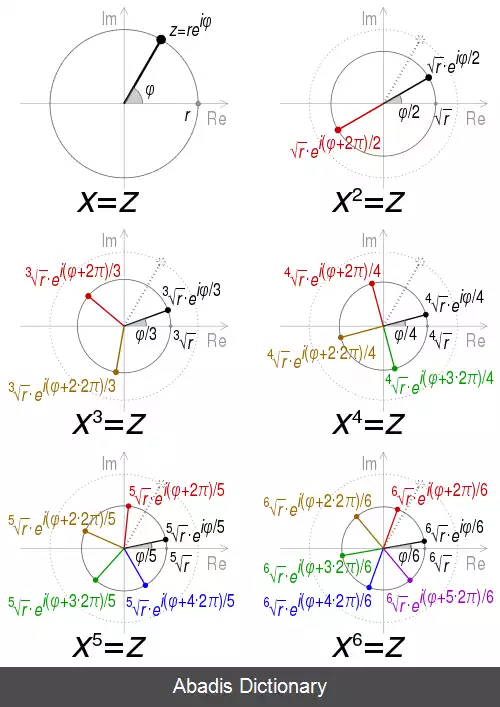
یک ریشه nام از واخد، که در آن n یک عدد صحیح مثبت است، یک عدد z است که معادله را زیر برآورده می کند:[ ۱] [ ۲]
بجز وقتیکه چیز دیگری تعیین شود، ریشه های واحد را می توان اعداد مختلط درنظر گرفت ( شامل عدد 1، و عدد - 1 اگر n زوج باشد ) ، که مختلطی با قسمت موهومی صفر هستند، و در این حالت، ریشه های nام از واحد به اینصورت هستند
با این حال، معادله تعریفی برای ریشه های واحد روی هر میدان F ( و حتی روی هر حلقه ای ) معنادار هستند، و این موضوع امکان درنظر گرفتن ریشه های واحد را در F را می دهد. میدان F هر چه باشد، ریشه های واحد در F دو حالت دارند: یا اعداد مختلط هستند، که وقتیکه مشخصه F صفر باشد رخ می دهد، یا در غیر اینصورت، به یک میدان متناهی تعلق دارند. برعکس، هر عنصر غیرصفر در یک میدان متناهی یک ریشه واحد در آن میدان است. ریشه واحد در پیمانه n و میدان متناهی را برای جزییات بیشتر ببینید.
یک ریشه nام واحد در صورتی اولیه ( primitive ) است که یک ریشه mام واحد برای یک m کوچکتر نباشد، یعنی اگر
اگر n یک عدد اول باشد، آنوقت همه ریشه های nام واحد، بجز 1، اصلی هستند.
در فرمول بالا به زبان توابع نمایی و مثلثاتی، ریشه های اصلی nام واحد آن هایی هستند که در آن k و n اعداد صحیح متباین هستند.
بخش های آتی این مقاله با ریشه های واحد مختلط مطابقت دارند. برای حالتی که ریشه های واحد در میدان هایی با مشخصه غیرصفر هستند، میدان متناهی § ریشه های واحد را ببینید. برای حالتی که ریشه های واحد در حلقه هایی از اعداد صحیح پیمانه ای هستند، ریشه واحد در پیمانه n را ببینید.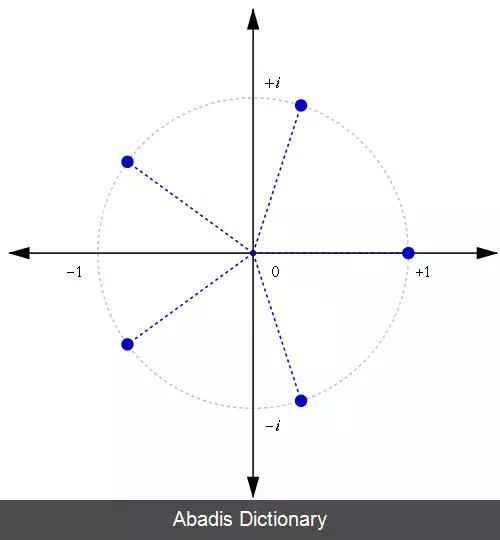
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفریشه واحد را در هر میدانی می توان تعریف کرد. اگر مشخصه میدان صفر باشد، ریشه ها اعداد مختلطی هستند که عدد صحیح جبری هم هستند. برای میدان های دارای مشخصه مثبت، ریشه ها به یک میدان متناهی تعلق دارند، و برعکس، هر عنصر غیرصفر از یک میدان متناهی یک ریشه واحد است. هر میدان بسته جبری دقیقا شامل n تا ریشه nام از واحد است، بجز وقتیکه n یک مضرب از مشخصه ( مثبت ) میدان باشد.
یک ریشه nام از واخد، که در آن n یک عدد صحیح مثبت است، یک عدد z است که معادله را زیر برآورده می کند:[ ۱] [ ۲]
بجز وقتیکه چیز دیگری تعیین شود، ریشه های واحد را می توان اعداد مختلط درنظر گرفت ( شامل عدد 1، و عدد - 1 اگر n زوج باشد ) ، که مختلطی با قسمت موهومی صفر هستند، و در این حالت، ریشه های nام از واحد به اینصورت هستند
با این حال، معادله تعریفی برای ریشه های واحد روی هر میدان F ( و حتی روی هر حلقه ای ) معنادار هستند، و این موضوع امکان درنظر گرفتن ریشه های واحد را در F را می دهد. میدان F هر چه باشد، ریشه های واحد در F دو حالت دارند: یا اعداد مختلط هستند، که وقتیکه مشخصه F صفر باشد رخ می دهد، یا در غیر اینصورت، به یک میدان متناهی تعلق دارند. برعکس، هر عنصر غیرصفر در یک میدان متناهی یک ریشه واحد در آن میدان است. ریشه واحد در پیمانه n و میدان متناهی را برای جزییات بیشتر ببینید.
یک ریشه nام واحد در صورتی اولیه ( primitive ) است که یک ریشه mام واحد برای یک m کوچکتر نباشد، یعنی اگر
اگر n یک عدد اول باشد، آنوقت همه ریشه های nام واحد، بجز 1، اصلی هستند.
در فرمول بالا به زبان توابع نمایی و مثلثاتی، ریشه های اصلی nام واحد آن هایی هستند که در آن k و n اعداد صحیح متباین هستند.
بخش های آتی این مقاله با ریشه های واحد مختلط مطابقت دارند. برای حالتی که ریشه های واحد در میدان هایی با مشخصه غیرصفر هستند، میدان متناهی § ریشه های واحد را ببینید. برای حالتی که ریشه های واحد در حلقه هایی از اعداد صحیح پیمانه ای هستند، ریشه واحد در پیمانه n را ببینید.


wiki: ریشه واحد
