حلقه چندجمله ای ( به انگلیسی: polynomial ring ) یا جبر حلقه ای، در ریاضیات، بخصوص در شاخه جبر، یک حلقه است ( از این رو یک جبر جابجایی هم هست ) که توسط مجموعه ای از چندجمله ای ها که یک یا چند نامعین دارند ( که به صورت سنتی متغیر نام دارند ) تشکیل شده که ضرایبشان در حلقهٔ دیگری است که معمولاً یک میدان است.
معمولاً اصطلاح «حلقه چندجمله ای» به صورت ضمنی به حالت خاصی از حلقه چندجمله ای اشاره دارد که یک نامعین روی یک میدان دارد. این حلقه های چندجمله ای به این علت مهم هستند که ویژگی های مشترکی زیادی است که با حلقه اعداد صحیح دارند.
حلقه چندجمله ای ها در شاخه های مختلفی از ریاضیات همچون نظریه اعداد، جبر جابجایی، و هندسه جبری ظهور پیدا می کنند. در نظریه حلقه ها، برای تعمیم بعضی ویژگی های حلقه های چندجمله ای، کلاس های مختلفی از حلقه ها معرفی شده اند که شامل: حوزه تجزیه یکتا، حلقه های منظم، حلقه های گروهی، حلقه های سری های توانی صوری، چند جمله ای های Ore و حلقه های مدرج هستند.
یک مفهوم بسیار مرتبط، حلقه توابع چندجمله ای روی فضای برداری، و به صورت کلی تر حلقه توابع منظم روی واریته جبری است.
حلقه چند جمله ای K، با X روی یک میدان ( یا به صورت کلی تر حلقه جابجایی ) K را می توان به صورت مجموعه ای از عبارات، که به آن چندجمله ای در X گفته می شود، به این حالت تعریف کرد ( تعاریف معادل دیگری هم وجود دارد که از آن ها هم استفاده معمول می شود ) :[ ۱]
که در آن p0, p1, …, pm یعنی ضرایب p عناصر K هستند و pm ≠ ۰ اگر m > 0 باشد و X , X 2 , . . . نمادهایی هستند که به عنوان «توان» X شناخته شده و از همان قواعد معمول به توان رساندن تبعیت می کنند، یعنی: X 0 = 1 و X 1 = X و برای هر عدد صحیح نامنفی k و l داریم: X k X l = X k + l . نماد X را نامعین[ ۲] یا متغیر[ ۳] می نامند ( اصطلاح «متغیر» از اصطلاح شناسی توابع چندجمله ای می آید. با این حال، در اینجا X هیچ مقداری ( غیر از خودش ) اختیار نمی کند و نمی تواند تغییر کند و در حلقه چندجمله ای ثابت است ) .
دو چند جمله ای زمانی با هم برابراند که ضرایب متناظر با هرکدام از Xk ها در هردو با هم برابر باشند.
حلقه چندجمله ای K را می توان به این صورت دید، که از میدان K با اضافه کردن یک عنصر جدید X ایجاد شده که این X برای K خارجی است و با همه عناصر K شرکت پذیر بوده و خاصیت ویژه دیگری هم ندارد ( از همین می توان برای تعریف کردن حلقه های چندجمله ای بهره جست ) .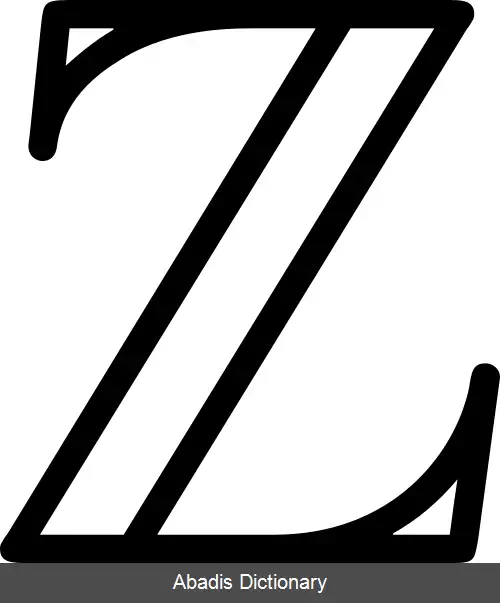
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمعمولاً اصطلاح «حلقه چندجمله ای» به صورت ضمنی به حالت خاصی از حلقه چندجمله ای اشاره دارد که یک نامعین روی یک میدان دارد. این حلقه های چندجمله ای به این علت مهم هستند که ویژگی های مشترکی زیادی است که با حلقه اعداد صحیح دارند.
حلقه چندجمله ای ها در شاخه های مختلفی از ریاضیات همچون نظریه اعداد، جبر جابجایی، و هندسه جبری ظهور پیدا می کنند. در نظریه حلقه ها، برای تعمیم بعضی ویژگی های حلقه های چندجمله ای، کلاس های مختلفی از حلقه ها معرفی شده اند که شامل: حوزه تجزیه یکتا، حلقه های منظم، حلقه های گروهی، حلقه های سری های توانی صوری، چند جمله ای های Ore و حلقه های مدرج هستند.
یک مفهوم بسیار مرتبط، حلقه توابع چندجمله ای روی فضای برداری، و به صورت کلی تر حلقه توابع منظم روی واریته جبری است.
حلقه چند جمله ای K، با X روی یک میدان ( یا به صورت کلی تر حلقه جابجایی ) K را می توان به صورت مجموعه ای از عبارات، که به آن چندجمله ای در X گفته می شود، به این حالت تعریف کرد ( تعاریف معادل دیگری هم وجود دارد که از آن ها هم استفاده معمول می شود ) :[ ۱]
که در آن p0, p1, …, pm یعنی ضرایب p عناصر K هستند و pm ≠ ۰ اگر m > 0 باشد و X , X 2 , . . . نمادهایی هستند که به عنوان «توان» X شناخته شده و از همان قواعد معمول به توان رساندن تبعیت می کنند، یعنی: X 0 = 1 و X 1 = X و برای هر عدد صحیح نامنفی k و l داریم: X k X l = X k + l . نماد X را نامعین[ ۲] یا متغیر[ ۳] می نامند ( اصطلاح «متغیر» از اصطلاح شناسی توابع چندجمله ای می آید. با این حال، در اینجا X هیچ مقداری ( غیر از خودش ) اختیار نمی کند و نمی تواند تغییر کند و در حلقه چندجمله ای ثابت است ) .
دو چند جمله ای زمانی با هم برابراند که ضرایب متناظر با هرکدام از Xk ها در هردو با هم برابر باشند.
حلقه چندجمله ای K را می توان به این صورت دید، که از میدان K با اضافه کردن یک عنصر جدید X ایجاد شده که این X برای K خارجی است و با همه عناصر K شرکت پذیر بوده و خاصیت ویژه دیگری هم ندارد ( از همین می توان برای تعریف کردن حلقه های چندجمله ای بهره جست ) .
wiki: حلقه چندجمله ای
