اعداد کاتالان در ریاضیات ترکیبی، یک سری از اعداد طبیعی هستند که در مسائل شمارشی متنوع که معمولاً اشیا به صورت بازگشتی تعریف شده را در بر می گیرند، رخ می دهند. این اعداد به افتخار ریاضیدان بلژیکی شارل کاتالان ( ۱۸۹۴ - ۱۸۱۴ ) اعداد کاتالان نامیده می شوند. وی استنتاج مقدماتی از فرمول را کشف کرد. کاتالان مقالات متعددی در زمینه آنالیز، ترکیبیات، جبر، هندسه، احتمالات و نظریه اعداد منتشر کرد. درستی حدس او که اعداد ۰، ۱، ۸، ۹ تنها زوج اعداد توان کامل متوالی است که به صورت توانی می باشد در دهه ۱۹۷۰ ثابت شد.
nاُمین عدد کاتالان عبارت است از:
چند عدد اولیه کاتالان عبارتند از:
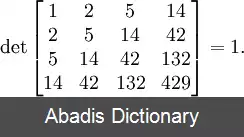
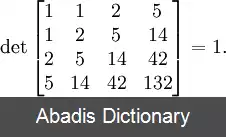
یک عبارت دیگر برای C n به صورت زیر است:
عبارت فوق نشان می دهد که C n یک عدد طبیعی است که این نتیجه از فرمول اول چندان بدیهی نبود. این عبارت اساس اثبات آندره در مورد صحت فرمول را تشکیل می دهد. هم چنین اعداد کاتالان از رابطه بازگشتی زیر نیز به دست می آیند:
و همچنین:
که می تواند برای محاسبه آن ها کاراتر باشد.
به طور مجانبی اعداد کاتالان به صورت C n ∼ 4 n n 3 / 2 π رشد می کنند که نشان می دهد که عبارت سمت راست برای ∞ →n به سمت یک میل می کند. ( این عبارت می تواند با استفاده از تقریب استرلینگ برای !n اثبات شود ) تنها اعدادی از دنباله کاتالان فرد هستند که به صورت n = 2 k − 1 هستند. بقیه همگی زوج می باشند.
تعداد زیادی از مسائل شمارشی در ترکیبیات هستند که راه حلی با استفاده از اعداد کاتالان برای آن ها ارائه شده است. کتاب ترکیبیات شمارشی جلد دوم اثر ریچارد استانلی شامل مجموعه ای از تمرین هاست که ۶۶ تفسیر مختلف از اعداد کاتالان را شرح می دهد. در زیر چند نمونه آمده است.
- C n تعداد کلمات Dyck به طول ۲n است. یک کلمه Dyck یک رشته است که n تاX و n تا Y دارد؛ به گونه ای که تعداد Xها در هر بخش آغازین آن بیشتر از تعداد Yهاست. برای مثال در زیر کلمات Dyck با طول ۶ آمده اند:
- چنانچه هر نماد X را به صورت یک پرانتز باز ببینیم و هر نماد Y را یک پرانتز بسته آنگاه C n تعداد عباراتی که شامل n جفت پرانتزگذاری صحیح هستند را نشان می دهد.
- C n تعداد راه های مختلفی است که n+۱ عامل می توانند پرانتزگذاری شوند. برای n=۳ به عنوان مثال ۵ پرانتزگذاری مختلف برای چهار عامل را داریم:
- C n تعداد درخت های دودویی غیر هم ریخت با n راس است که بچه دارند که معمولاً رئوس داخلی یا شاخه گفته می شوند.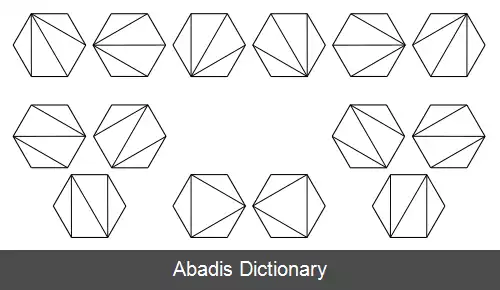
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفnاُمین عدد کاتالان عبارت است از:
چند عدد اولیه کاتالان عبارتند از:
یک عبارت دیگر برای C n به صورت زیر است:
عبارت فوق نشان می دهد که C n یک عدد طبیعی است که این نتیجه از فرمول اول چندان بدیهی نبود. این عبارت اساس اثبات آندره در مورد صحت فرمول را تشکیل می دهد. هم چنین اعداد کاتالان از رابطه بازگشتی زیر نیز به دست می آیند:
و همچنین:
که می تواند برای محاسبه آن ها کاراتر باشد.
به طور مجانبی اعداد کاتالان به صورت C n ∼ 4 n n 3 / 2 π رشد می کنند که نشان می دهد که عبارت سمت راست برای ∞ →n به سمت یک میل می کند. ( این عبارت می تواند با استفاده از تقریب استرلینگ برای !n اثبات شود ) تنها اعدادی از دنباله کاتالان فرد هستند که به صورت n = 2 k − 1 هستند. بقیه همگی زوج می باشند.
تعداد زیادی از مسائل شمارشی در ترکیبیات هستند که راه حلی با استفاده از اعداد کاتالان برای آن ها ارائه شده است. کتاب ترکیبیات شمارشی جلد دوم اثر ریچارد استانلی شامل مجموعه ای از تمرین هاست که ۶۶ تفسیر مختلف از اعداد کاتالان را شرح می دهد. در زیر چند نمونه آمده است.
- C n تعداد کلمات Dyck به طول ۲n است. یک کلمه Dyck یک رشته است که n تاX و n تا Y دارد؛ به گونه ای که تعداد Xها در هر بخش آغازین آن بیشتر از تعداد Yهاست. برای مثال در زیر کلمات Dyck با طول ۶ آمده اند:
- چنانچه هر نماد X را به صورت یک پرانتز باز ببینیم و هر نماد Y را یک پرانتز بسته آنگاه C n تعداد عباراتی که شامل n جفت پرانتزگذاری صحیح هستند را نشان می دهد.
- C n تعداد راه های مختلفی است که n+۱ عامل می توانند پرانتزگذاری شوند. برای n=۳ به عنوان مثال ۵ پرانتزگذاری مختلف برای چهار عامل را داریم:
- C n تعداد درخت های دودویی غیر هم ریخت با n راس است که بچه دارند که معمولاً رئوس داخلی یا شاخه گفته می شوند.



wiki: اعداد کاتالان
