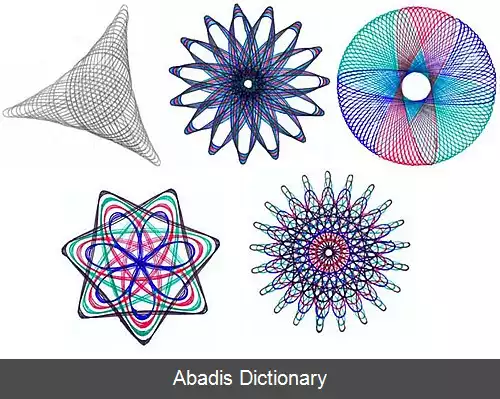
اسپیروگراف ( به انگلیسی: Spirograph ) یا اسپیرونگار یا چرخ نگار یا زُرفین نگار که در ایران با نام دوایر جادوییِ اقلیدس شناخته می شود، نوعی اسباب بازی است که برای کشیدن اَشکال هندسیِ پدیدآمده از منحنی های ریاضی با روشِ درون چرخه زاد به کار می رود. اسپیروگراف اولین بار به دست دنیس فیشر گسترش یافت و در سال ۱۹۶۵ به بازار ارائه شد.
از واژهٔ اسپیروگراف برای نام بردن از گسترهٔ ابزارهایی که برای کشیدن چنین اشکالی به کار می روند هم استفاده می شود. حتی می تواند برای نامیدن منحنی های درون چرخه زاد نیز به کار رود. اسپیروگراف از زمان خریده شدنِ شرکت دنیس فیشر به دست شرکت اسباب بازی سازی هازبرو، یک نشان تجاری ثبت شدهٔ شرکت هازبرو است.
ابزاری با نام اسپیروگراف ابتدا در سال های ۱۸۸۱ تا ۱۹۰۰ به دست ریاضیدانی به نام برونو آباکانویچ برای به دست آوردن مساحت زیر منحنی ساخته شد. [ ۱] اسباب بازی های کشیدنِ اَشکال با چرخ دنده حداقل از سال ۱۹۰۸ وجود داشته اند؛ در این سال ها تبلیغات ابزاری با نام «مارولوس وندرگراف» با کارکردی مشابه در کاتالوگ فروشگاه سیرز چاپ می شده است. [ ۲] [ ۳] مجلهٔ مکانیک پسران در سال ۱۹۱۳ نوشتاری چاپ کرد که چگونگی ساخت ماشینی برای کشیدن وندرگراف را توضیح می دهد. [ ۴] اما اسپیروگرافِ امروزی به دست مهندس انگلیسی، دنیس فیشر، گسترش یافته و اولین بار در سال ۱۹۶۵ در نمایشگاه بین المللی اسباب بازی نورنبرگ نمایش داده شد. پس از آن، در شرکت خودِ او ساخته شد و امتیاز پخش آن به شرکت اسباب بازی کنر داده شد که در سال ۱۹۶۶ فروش آن را در آمریکا با تبلیغ اسباب بازی نوآورانهٔ کودکان شروع کرد.
در سال ۱۹۶۸، «کنر» اسباب بازی «اسپیروتات» را ساخت که نسخه ای ساده شده از اسپیروگراف برای کودکانِ پیش از دبستان بود.
اسپیروگراف شامل قطعاتی است که معمولاً آن ها را با پلاستیک می سازند و به صورت دایرهای یا دایره های بزرگ توخالی، مثلثی، میلهای و غیره هستند. در اطراف همهٔ آن ها دندانههایی وجود دارد که باعث می شود در داخل یا محیط دایره های بزرگ بتوان آن ها را چرخاند. در داخل قطعات معمولاً سوراخ هایی وجود دارد که محل قرار گرفتن نوک قلم است و اَشکال مختلف از آن ها ایجاد می شود.
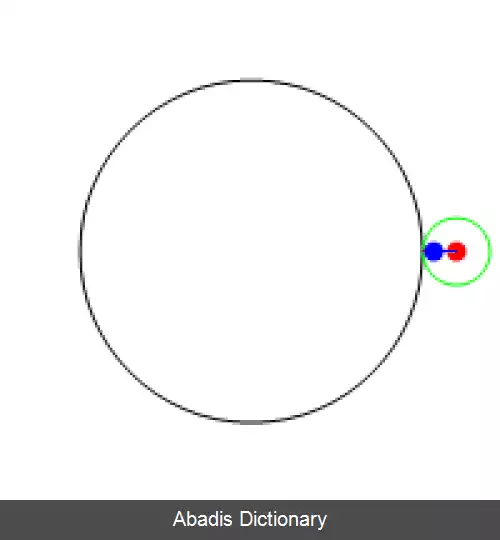
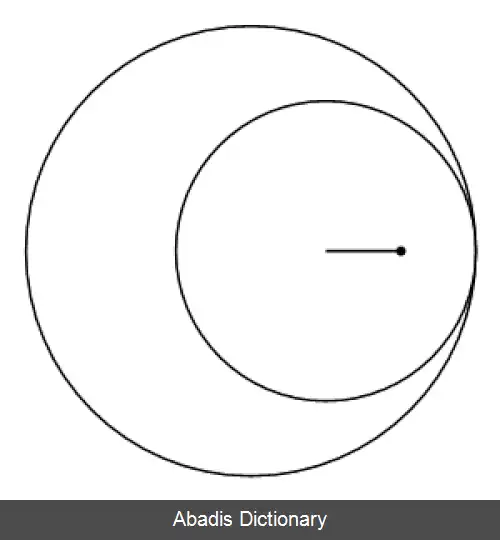
دایرهٔ ثابت C 1 با شعاع R را در نظر بگیرید. دایرهٔ کوچک تر C 2 با شعاع r < R در داخل دایرهٔ اول به صورت مماس بر آن می گردد. فرض کنید که نقطهٔ A در داخل دایرهٔ کوچک تر در فاصلهٔ ρ < r از مرکز آن قرار گرفته باشد. فرض می کنیم که نقطهٔ A ابتدا بر محور Xها بوده است. طرح حاصل از اسپیروگراف از خط سیر نقطهٔ A در داخل دایرهٔ بزرگ به دست می آید.


این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز واژهٔ اسپیروگراف برای نام بردن از گسترهٔ ابزارهایی که برای کشیدن چنین اشکالی به کار می روند هم استفاده می شود. حتی می تواند برای نامیدن منحنی های درون چرخه زاد نیز به کار رود. اسپیروگراف از زمان خریده شدنِ شرکت دنیس فیشر به دست شرکت اسباب بازی سازی هازبرو، یک نشان تجاری ثبت شدهٔ شرکت هازبرو است.
ابزاری با نام اسپیروگراف ابتدا در سال های ۱۸۸۱ تا ۱۹۰۰ به دست ریاضیدانی به نام برونو آباکانویچ برای به دست آوردن مساحت زیر منحنی ساخته شد. [ ۱] اسباب بازی های کشیدنِ اَشکال با چرخ دنده حداقل از سال ۱۹۰۸ وجود داشته اند؛ در این سال ها تبلیغات ابزاری با نام «مارولوس وندرگراف» با کارکردی مشابه در کاتالوگ فروشگاه سیرز چاپ می شده است. [ ۲] [ ۳] مجلهٔ مکانیک پسران در سال ۱۹۱۳ نوشتاری چاپ کرد که چگونگی ساخت ماشینی برای کشیدن وندرگراف را توضیح می دهد. [ ۴] اما اسپیروگرافِ امروزی به دست مهندس انگلیسی، دنیس فیشر، گسترش یافته و اولین بار در سال ۱۹۶۵ در نمایشگاه بین المللی اسباب بازی نورنبرگ نمایش داده شد. پس از آن، در شرکت خودِ او ساخته شد و امتیاز پخش آن به شرکت اسباب بازی کنر داده شد که در سال ۱۹۶۶ فروش آن را در آمریکا با تبلیغ اسباب بازی نوآورانهٔ کودکان شروع کرد.
در سال ۱۹۶۸، «کنر» اسباب بازی «اسپیروتات» را ساخت که نسخه ای ساده شده از اسپیروگراف برای کودکانِ پیش از دبستان بود.
اسپیروگراف شامل قطعاتی است که معمولاً آن ها را با پلاستیک می سازند و به صورت دایرهای یا دایره های بزرگ توخالی، مثلثی، میلهای و غیره هستند. در اطراف همهٔ آن ها دندانههایی وجود دارد که باعث می شود در داخل یا محیط دایره های بزرگ بتوان آن ها را چرخاند. در داخل قطعات معمولاً سوراخ هایی وجود دارد که محل قرار گرفتن نوک قلم است و اَشکال مختلف از آن ها ایجاد می شود.
دایرهٔ ثابت C 1 با شعاع R را در نظر بگیرید. دایرهٔ کوچک تر C 2 با شعاع r < R در داخل دایرهٔ اول به صورت مماس بر آن می گردد. فرض کنید که نقطهٔ A در داخل دایرهٔ کوچک تر در فاصلهٔ ρ < r از مرکز آن قرار گرفته باشد. فرض می کنیم که نقطهٔ A ابتدا بر محور Xها بوده است. طرح حاصل از اسپیروگراف از خط سیر نقطهٔ A در داخل دایرهٔ بزرگ به دست می آید.






wiki: اسپیروگراف
