در هندسه چندضلعی محدب[ ۱] [ ۲] ( انگلیسی: Convex polygon ) یا چند گوش کوژ گونه ای چند گوش است که مرز یک مجموعه ی کوژ به شمار می رود. در هندسه یک چند گوشِ ساده می تواند کوژ ( محدب ) یا کاو ( مقعر ) باشد. در کوژ همه ی گوشه های درونی کمتر از ۱۸۰º است ( سه گوش و… ) . اگر دیسی دست کم یکی از گوشه های درونی اش از ۱۸۰º بزرگ تر باشد، دیس ( شکل ) کاو یا مقعر نامیده می شود.
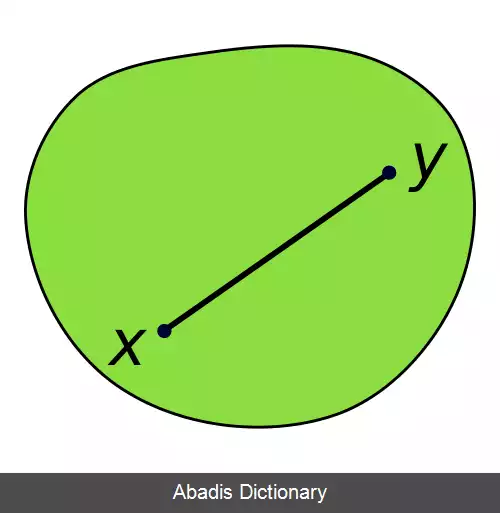
چند گوش کوژ یک چند گوش ساده است که پهنه ( سطح ) آن یک مجموعه ی کوژ را می سازد، به گویش دیگر، باید بتوان از هر دو نقطه درون چند گوش ( کوژ ) خطی میان آن دو نقطه کشید به گونه ای که همه ی آن پاره خط درون چند گوش باشد.
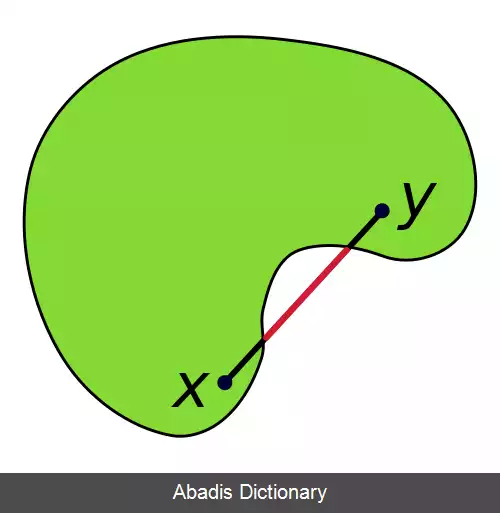
• خط پیوند دهنده ی میان هر دو نقطه ی دلخواه درون یا روی چند گوش، به درستی درون یا روی چند گوش جا گرفته باشد.
• اگر یکی از بَر ها را ادامه دهیم دیس ( شکل ) را برش نمی دهد.
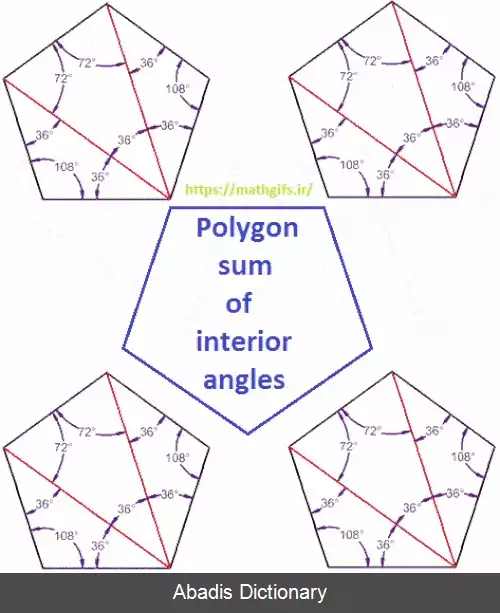
برای برآورد جمع گوشه های درونی چند گوش آن را سه گوش بندی می کنیم. از یک سر آن به دیگر سر ها پیوند داده و شمار سه گوش های به دست آمده را در ۱۸۰º ضرب می کنیم. به گویش دیگر داریم: ( n − 2 ) × 180
همچنین برای به دست آوردن اندازه ی هر گوشه ی درونی یک چند گوش منتظم ( همگون ) بایستی این مجموع را به شمار بَر ها بخش ( تقسیم ) کنیم: ( n − 2 ) × 180 n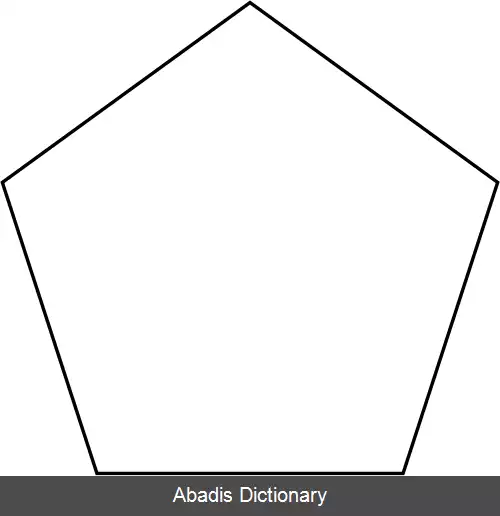

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفچند گوش کوژ یک چند گوش ساده است که پهنه ( سطح ) آن یک مجموعه ی کوژ را می سازد، به گویش دیگر، باید بتوان از هر دو نقطه درون چند گوش ( کوژ ) خطی میان آن دو نقطه کشید به گونه ای که همه ی آن پاره خط درون چند گوش باشد.
• خط پیوند دهنده ی میان هر دو نقطه ی دلخواه درون یا روی چند گوش، به درستی درون یا روی چند گوش جا گرفته باشد.
• اگر یکی از بَر ها را ادامه دهیم دیس ( شکل ) را برش نمی دهد.
برای برآورد جمع گوشه های درونی چند گوش آن را سه گوش بندی می کنیم. از یک سر آن به دیگر سر ها پیوند داده و شمار سه گوش های به دست آمده را در ۱۸۰º ضرب می کنیم. به گویش دیگر داریم: ( n − 2 ) × 180
همچنین برای به دست آوردن اندازه ی هر گوشه ی درونی یک چند گوش منتظم ( همگون ) بایستی این مجموع را به شمار بَر ها بخش ( تقسیم ) کنیم: ( n − 2 ) × 180 n





wiki: چندضلعی محدب
