پل خربگیری
لغت نامه دهخدا
دانشنامه عمومی
پل خربگیری یا پونس اسینوروم ( لاتین: Pons asinorum ) پنجمین قضیه در مقالهٔ اول اصول اقلیدس است و بیان می کند که زوایای مقابل به ساق مثلث متساوی الساقین با هم برابرند. عکس این قضیه هم درست است، یعنی اگر دو زاویهٔ مثلثی با هم مساوی باشند اضلاع متقابل آن زوایا هم با هم مساوی اند.
عنوان این قضیه اشاره به این موضوع دارد که این قضیه اولین مسئله نسبتاً دشوار در اصول اقلیدس است و بسیاری از افراد آن را درک نمی کردند و با رسیدن به آن، همچون خری که روی پل مانده باشد، دیگر جلو نمی رفتند. این عبارت امروزه به ضرب المثلی تبدیل شده و به مسئله یا چالشی اشاره دارد که محکی برای جداسازی متخصصان و مجرب ها از مبتدیان است.
اگر ABC مثلثی متساوی الساقین باشد، دو ساق آن، یعنی AC و AB برابرند. مراد این است که ثابت شود دو زاویهٔ قاعده این مثلث، یعنی زاویه های C و B، برابرند.
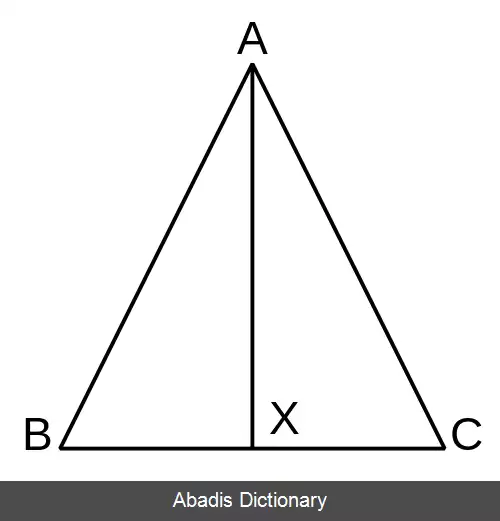
برهان قضیه با ترسیم خط AX، که زاویه A را نصف می کند، آغاز می شود.
درستی این مرحله از کار بدین خاطر است که اقلیدس پیش تر نشان داده است که هر زاویه ای را می توان نصف کرد؛ بنابراین، C را نیز می توان به دو قسمت مساوی تقسیم کرد.
با ترسیم خط AX مثلث ABC به دو مثلث AXC و AXB تقسیم می شود. در مورد این دو مثلث اخیر می دانیم که:
اولاً AC با AB برابر است، زیرا گفته بودیم که مثلث نخستین، یعنی مثلث ABC، متساوی الساقین است.
ثانیاً زاویه CAX مساوی با زاویه BAX است، زیرا AX نیمساز زاویه است.
ثالثاً از آن جا که AX بین دو مثلث کوچک تر مشترک است، این ضلع آن دو مثلث برابرند.
بنابراین می توانیم حکم کنیم که دو مثلث AXC و AXB هم نهشت هستند، زیرا پیش از قضیه مورد بحث در کتاب اصول قضیه ای هست که حکم می کند هر دو مثلثی که دو ضلع و زاویه بین آن ها از یکی با دو ضلع و زاویه بینشان از دیگری برابر باشند هم نهشت اند، و از آن جا که دو مثلث مورد بحث چنین قسمت های برابری دارند، هم نهشت هستند.
سرانجام می توان حکم کرد که زاویه B مساوی زاویه C است، زیرا بنا به تعریف مثلث های هم نهشت بخش های متناظر مساویند و زاویه های C و B چنین بخش هایی هستند. به این ترتیب، قضیه مورد بحث با چند دلیل استنتاجی که هر یک از آن ها فرضی بی تردید را به خدمت می گیرد و نتیجه ای بی تردید را به بار می آورد، ثابت می شود.
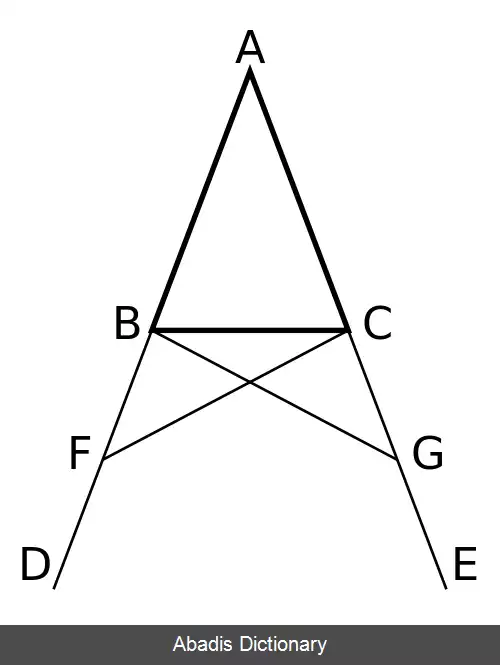
اثبات این قضیه در اصول اقلیدس نتیجهٔ دیگری نیز دارد و آن این است که اگر ساق ها را امتداد دهیم زوایای میان قاعده و امتداد ساق ها نیز با هم برابر می شوند.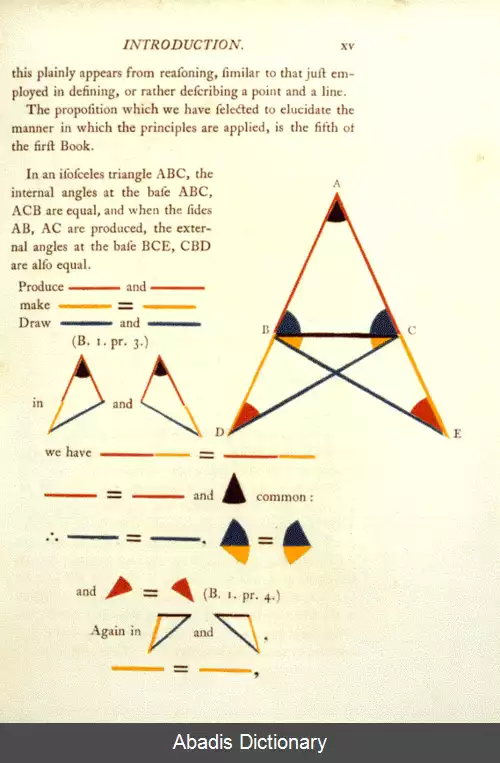

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفعنوان این قضیه اشاره به این موضوع دارد که این قضیه اولین مسئله نسبتاً دشوار در اصول اقلیدس است و بسیاری از افراد آن را درک نمی کردند و با رسیدن به آن، همچون خری که روی پل مانده باشد، دیگر جلو نمی رفتند. این عبارت امروزه به ضرب المثلی تبدیل شده و به مسئله یا چالشی اشاره دارد که محکی برای جداسازی متخصصان و مجرب ها از مبتدیان است.
اگر ABC مثلثی متساوی الساقین باشد، دو ساق آن، یعنی AC و AB برابرند. مراد این است که ثابت شود دو زاویهٔ قاعده این مثلث، یعنی زاویه های C و B، برابرند.
برهان قضیه با ترسیم خط AX، که زاویه A را نصف می کند، آغاز می شود.
درستی این مرحله از کار بدین خاطر است که اقلیدس پیش تر نشان داده است که هر زاویه ای را می توان نصف کرد؛ بنابراین، C را نیز می توان به دو قسمت مساوی تقسیم کرد.
با ترسیم خط AX مثلث ABC به دو مثلث AXC و AXB تقسیم می شود. در مورد این دو مثلث اخیر می دانیم که:
اولاً AC با AB برابر است، زیرا گفته بودیم که مثلث نخستین، یعنی مثلث ABC، متساوی الساقین است.
ثانیاً زاویه CAX مساوی با زاویه BAX است، زیرا AX نیمساز زاویه است.
ثالثاً از آن جا که AX بین دو مثلث کوچک تر مشترک است، این ضلع آن دو مثلث برابرند.
بنابراین می توانیم حکم کنیم که دو مثلث AXC و AXB هم نهشت هستند، زیرا پیش از قضیه مورد بحث در کتاب اصول قضیه ای هست که حکم می کند هر دو مثلثی که دو ضلع و زاویه بین آن ها از یکی با دو ضلع و زاویه بینشان از دیگری برابر باشند هم نهشت اند، و از آن جا که دو مثلث مورد بحث چنین قسمت های برابری دارند، هم نهشت هستند.
سرانجام می توان حکم کرد که زاویه B مساوی زاویه C است، زیرا بنا به تعریف مثلث های هم نهشت بخش های متناظر مساویند و زاویه های C و B چنین بخش هایی هستند. به این ترتیب، قضیه مورد بحث با چند دلیل استنتاجی که هر یک از آن ها فرضی بی تردید را به خدمت می گیرد و نتیجه ای بی تردید را به بار می آورد، ثابت می شود.
اثبات این قضیه در اصول اقلیدس نتیجهٔ دیگری نیز دارد و آن این است که اگر ساق ها را امتداد دهیم زوایای میان قاعده و امتداد ساق ها نیز با هم برابر می شوند.





wiki: پل خربگیری
پیشنهاد کاربران
پل خر بگیری : [عامیانه، اصطلاح] محل آزمایش، جایی که گریز از آن ممکن نباشد.
