هندسه اقلیدسی
لغت نامه دهخدا
توضیح : اصل موضوع اقلیدس عبارت است از این فرضیه : از یک نقطه خارج خطی فقط یک خط می توان موازی آن رسم کرد.
فرهنگ فارسی
دانشنامه عمومی
هندسه اقلیدس ( به انگلیسی: Euclidean Geometry ) دستگاهی ریاضیاتی است که آن را به اقلیدس، ریاضیدان یونانی اهل اسکندریه نسبت می دهند؛ چرا که او در کتاب هندسه خود به نام اصول اقلیدس ( Elements ) این نوع هندسه را توصیف نمود. روش اقلیدس شامل فرض گرفتن دسته کوچکی از اصول موضوعه های شهودی، و استنتاج گزاره های زیادی از این اصول می باشد. گرچه که بسیاری از نتایج اقلیدس توسط ریاضیدانان قبل تر از او هم بیان شده بودند، [ ۱] اقلیدس اولین کسی بود که که نشان داد چگونه می توان این گزاره ها را در یک دستگاه استنتاجی و منطقی جامع گنجاند. [ ۲] کتاب اصول اقلیدس، ابتدا از هندسه مسطحه شروع می کند که هنوز هم در آموزش متوسطه به عنوان اولین دستگاه اصول موضوعه ای و اولین مثال ها از اثبات های ریاضیاتی تدریس می گردند. سپس این کتاب به مباحث اجسام صلب از فضای سه بعدی می پردازد. بخش اعظم کتاب اصول اقلیدس به بیان نتایجی می پردازد که اکنون به آن جبر و نظریه اعداد گفته شده و در آنجا به زبان هندسی بیان شده اند. [ ۱]
برای بیش از دو هزار سال، صفت «اقلیدسی» برای چنین هندسه ای غیر ضروری می نمود، چرا که هیچ نوع هندسه دیگری هنوز درک نشده بود. اصول موضوعه های اقلیدس بسیار واضح و شهودی به نظر می رسیدند ( به جز احتمالاً اصل توازی ) به گونه ای که هر قضیه ای که از آن ها منتج می شد، با حالتی مطلق و عمدتاً ماورائی مورد پذیرش و مقبولیت قرار می گرفت. با این حال، امروزه بسیاری از هندسه های خود - سازگار و نااقلیدسی نیز شناخته شده اند که ابتدا در اوایل قرن ۱۹م میلادی کشف شدند. نظریه نسبیت عام آلبرت اینشتین دلالت بر این دارد که فضای فیزیکی به خودی خود اقلیدسی نبوده، و فضای اقلیدسی در فواصل کوتاه ( نسبت به میدان گرانشی ) ، تقریب خوبی برای آن است. [ ۳]
هندسه اقلیدسی مثالی از هندسه سنتتیک ( Synthetic Geometry ) است، اینگونه که از نظر منطقی می توان از اصول موضوعه های توصیف کننده خواص پایه ای اشیاء هندسی چون نقاط و خطوط، به گزاره های توصیف کننده خواص آن اشیاء دست یافت که همگی این استدلالات بدون استفاده از دستگاه مختصات برای تعیین آن اشیاء صورت می پذیرد. این را می توان با هندسه تحلیلی مقایسه نمود که در آن مختصات را جهت ترجمه گزاره های هندسی به زبان فرمول های جبری مورد استفاده قرار می دهند.
در حدود ۳۰۱ سال قبل از میلاد دنیای هندسه در تب و تاب بود. نظرات مختلفی در زمینهٔ هندسه وجود داشت و سرانجام اقلیدس با انتشار کتاب اصول بنیادی را بنا نهاد که تا قرن ها منسجم ترین بنیادهای نظری بشر محسوب می شد. روش اقلیدس ساده بود او چند اصل موضوع و چند اصل متعارف را بدون اثبات به عنوان اصول بدیهی پذیرفت و سپس بر اساس آن صدها قضیه دیگر را اثبات کرد که بیشتر آن ها بسیار دور از ذهن بودند.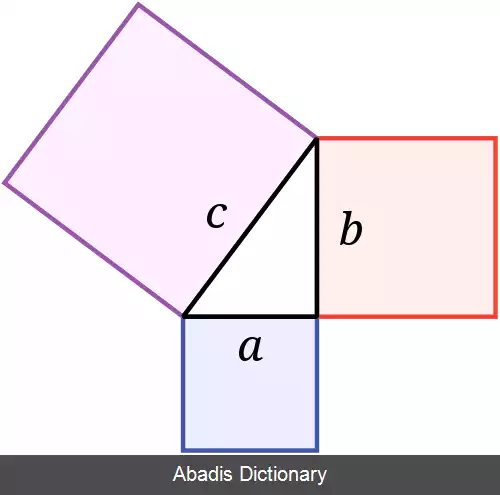

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای بیش از دو هزار سال، صفت «اقلیدسی» برای چنین هندسه ای غیر ضروری می نمود، چرا که هیچ نوع هندسه دیگری هنوز درک نشده بود. اصول موضوعه های اقلیدس بسیار واضح و شهودی به نظر می رسیدند ( به جز احتمالاً اصل توازی ) به گونه ای که هر قضیه ای که از آن ها منتج می شد، با حالتی مطلق و عمدتاً ماورائی مورد پذیرش و مقبولیت قرار می گرفت. با این حال، امروزه بسیاری از هندسه های خود - سازگار و نااقلیدسی نیز شناخته شده اند که ابتدا در اوایل قرن ۱۹م میلادی کشف شدند. نظریه نسبیت عام آلبرت اینشتین دلالت بر این دارد که فضای فیزیکی به خودی خود اقلیدسی نبوده، و فضای اقلیدسی در فواصل کوتاه ( نسبت به میدان گرانشی ) ، تقریب خوبی برای آن است. [ ۳]
هندسه اقلیدسی مثالی از هندسه سنتتیک ( Synthetic Geometry ) است، اینگونه که از نظر منطقی می توان از اصول موضوعه های توصیف کننده خواص پایه ای اشیاء هندسی چون نقاط و خطوط، به گزاره های توصیف کننده خواص آن اشیاء دست یافت که همگی این استدلالات بدون استفاده از دستگاه مختصات برای تعیین آن اشیاء صورت می پذیرد. این را می توان با هندسه تحلیلی مقایسه نمود که در آن مختصات را جهت ترجمه گزاره های هندسی به زبان فرمول های جبری مورد استفاده قرار می دهند.
در حدود ۳۰۱ سال قبل از میلاد دنیای هندسه در تب و تاب بود. نظرات مختلفی در زمینهٔ هندسه وجود داشت و سرانجام اقلیدس با انتشار کتاب اصول بنیادی را بنا نهاد که تا قرن ها منسجم ترین بنیادهای نظری بشر محسوب می شد. روش اقلیدس ساده بود او چند اصل موضوع و چند اصل متعارف را بدون اثبات به عنوان اصول بدیهی پذیرفت و سپس بر اساس آن صدها قضیه دیگر را اثبات کرد که بیشتر آن ها بسیار دور از ذهن بودند.




wiki: هندسه اقلیدسی
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
