همضرب (نظریه رسته ها). همضرب ( به انگلیسی: coproduct ) یا جمع رسته ای در نظریه رسته ها، یک ساختار است که به عنوان مثال می تواند اجتماع مجزای مجموعه ها، و در فضاهای توپولوژیکی همان ضرب آزاد گروه ها، و جمع مستقیم مدول ها و فضاهای برداری باشد. همضرب برای خانواده ای از اشیاء، اساساً برابر «خاص ترین» شیءای است که در آن، هر شیء در خانواده یک ریختار را می پذیرد. این مفهوم دوگان رسته - نظری برای ضرب رسته ای است، که یعنی تعریف آن مشابه ضرب است اما در آن همه پیکان ها معکوس شده اند. علیرغم این تغییر بظاهر بدون ضرر در نام و نماد، همضرب گاهی ( و معمولاً به صورت چشمگیر ) با ضرب متفاوت است.
فرض کنید که C یک رسته باشد، و فرض کنید که X 1 و X 2 برابر اشیای C باشند. یک شیء همضرب X 1 و X 2 نامیده می شود و به صورت X 1 ∐ X 2 یا X 1 ⊕ X 2 یا گاهی به صورت ساده X 1 + X 2 نوشته می شود اگر یک ریختار i 1 : X 1 → X 1 ∐ X 2 و i 2 : X 2 → X 1 ∐ X 2 موجود باشد که این ویژگی جهانی را برآورده سازد: برای هر شیء Y و هر ریختار f 1 : X 1 → Y و f 2 : X 2 → Y یک ریختار یکتا f : X 1 ∐ X 2 → Y موجود است به این صورت که f 1 = f ∘ i 1 و f 2 = f ∘ i 2 است؛ یعنی، نمودار زیر جابجایی است:
پیکان یکتای f که نمودار را جابجایی می سازد، را می توان به صورت f 1 ∐ f 2 , f 1 ⊕ f 2 , f 1 + f 2 , یا نمایش داد. ریختارهای i 1 و i 2 یک به یک کانونی نامیده می شوند، اگرچه نیازی نیست که یک به یک یا حتی مونو باشند.
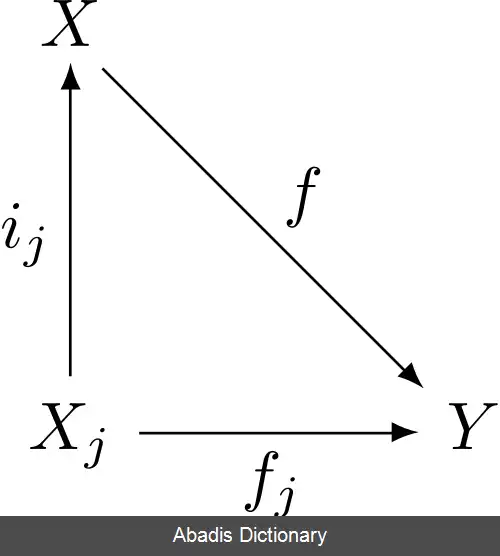
تعریف یک همضرب را می توان به خانواده دلخواهی از اشیاء که توسط J اندیس دهی شده اند تعمیم داد. همضرب خانواده { X j : j ∈ J } برابر شیء X همراه با یک گردآورد از ریختارها i j : X j → X است به این صورت که، برای هر شیء Y و هر گردآورد از ریختارها f j : X j → Y یک ریختار یکتا f : X → Y وجود دارد به اینصورت که f j = f ∘ i j است؛ یعنی، نمودار زیر برای هر j ∈ J جابجایی پذیر باشد:
همضرب X برای خانواده { X j } را معمولاً توسط ∐ j ∈ J X j یا ⨁ j ∈ J X j نمایش می دهند.
گاهی ریختار f : X → Y را به صورت ∐ j ∈ J f j نشان می دهند تا وابستگی آن را به f j های منفرد نشان بدهند.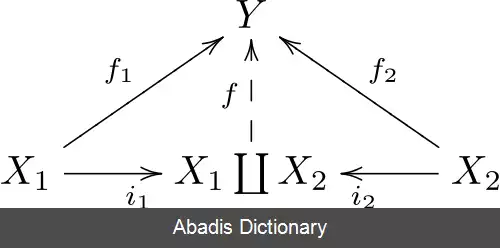
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید که C یک رسته باشد، و فرض کنید که X 1 و X 2 برابر اشیای C باشند. یک شیء همضرب X 1 و X 2 نامیده می شود و به صورت X 1 ∐ X 2 یا X 1 ⊕ X 2 یا گاهی به صورت ساده X 1 + X 2 نوشته می شود اگر یک ریختار i 1 : X 1 → X 1 ∐ X 2 و i 2 : X 2 → X 1 ∐ X 2 موجود باشد که این ویژگی جهانی را برآورده سازد: برای هر شیء Y و هر ریختار f 1 : X 1 → Y و f 2 : X 2 → Y یک ریختار یکتا f : X 1 ∐ X 2 → Y موجود است به این صورت که f 1 = f ∘ i 1 و f 2 = f ∘ i 2 است؛ یعنی، نمودار زیر جابجایی است:
پیکان یکتای f که نمودار را جابجایی می سازد، را می توان به صورت f 1 ∐ f 2 , f 1 ⊕ f 2 , f 1 + f 2 , یا نمایش داد. ریختارهای i 1 و i 2 یک به یک کانونی نامیده می شوند، اگرچه نیازی نیست که یک به یک یا حتی مونو باشند.
تعریف یک همضرب را می توان به خانواده دلخواهی از اشیاء که توسط J اندیس دهی شده اند تعمیم داد. همضرب خانواده { X j : j ∈ J } برابر شیء X همراه با یک گردآورد از ریختارها i j : X j → X است به این صورت که، برای هر شیء Y و هر گردآورد از ریختارها f j : X j → Y یک ریختار یکتا f : X → Y وجود دارد به اینصورت که f j = f ∘ i j است؛ یعنی، نمودار زیر برای هر j ∈ J جابجایی پذیر باشد:
همضرب X برای خانواده { X j } را معمولاً توسط ∐ j ∈ J X j یا ⨁ j ∈ J X j نمایش می دهند.
گاهی ریختار f : X → Y را به صورت ∐ j ∈ J f j نشان می دهند تا وابستگی آن را به f j های منفرد نشان بدهند.


wiki: همضرب (نظریه رسته ها)
