هذلولی

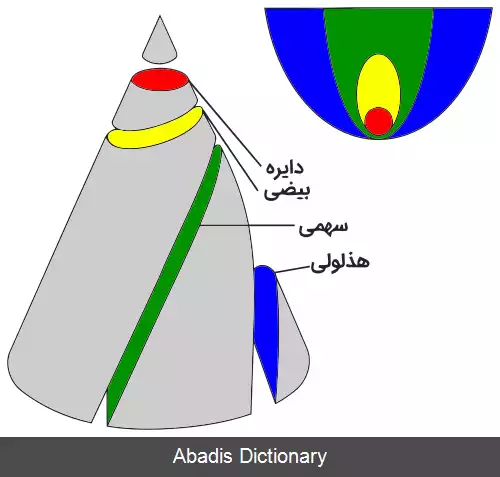
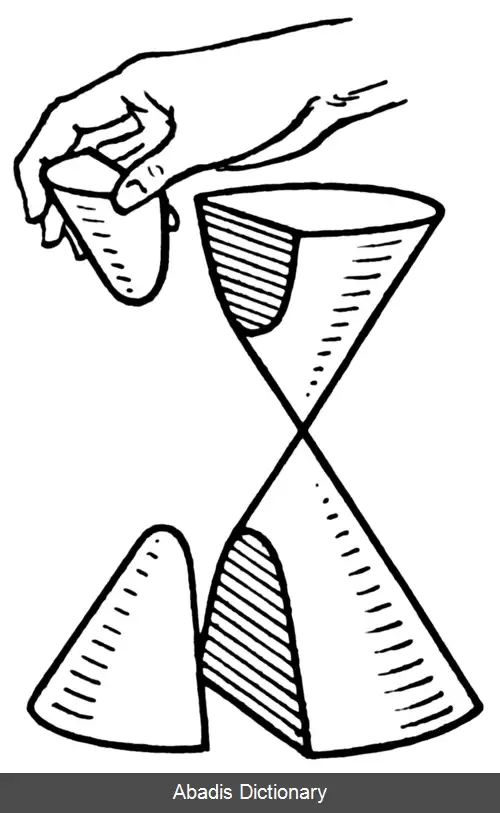
هُذلولی یا اَبَرپَرته[ ۱] ( برگردانِ گرته برداشته ) ( به انگلیسی: Hyperbola ) ، خمی باز است که از برخورد یک صفحه با سطح مخروطی، در حالتی که صفحه، موازی با محورِ سطحِ مخروطی باشد، پدید می آید. در صفحهٔ اقلیدسی و از نظر مکان هندسی، هذلولی مجموعه ای از نقاط در یک صفحه است که تفاضل فاصلهٔ هر یک از آن ها از دو نقطهٔ ثابت در صفحه ( کانون ها ) ، مقداری ثابت ( دو برابر مقدار a در هذلولی ) باشد؛ اگر نصف اندازهٔ طول و عرض هذلولی را a و b و نصف فاصلهٔ کانونی را c بنامیم، در هر هذلولی رابطهٔ c2 = a2 + b2 برقرار خواهد بود. هر هذلولی دو خط مجانب دارد که در مرکز هذلولی با هم برخورد می کنند.
بنابر تقریظی از اراتوستن، هذلولی را نخستین بار منایخموس ( ۳۸۰–۳۲۰ پ. م ) ، دوست نزدیک افلاطون، در تلاش برای حل تضعیف مکعب ( ساختن مکعبی که حجم آن دو برابر حجم یک مکعب مفروض است فقط با استفاده از خط کش و پرگار ) کشف کرد. آپولونیوس برای اولین بار نام «اوپربولی» ( ( به یونانی: υπερβολή ) ، به معنای «بیشتر بودن» ) [ الف] را بر روی هذلولی گذاشت[ ۲] و اقلیدس ( حدود ۳۶۵–۲۷۵ پ. م ) بررسی دقیقی از ویژگی های هذلولی ارائه کرد. [ ۳] پاپوس اسکندرانی ( حدود ۳۵۰ — ۲۹۰ پ. م ) مفهوم خط های هادی را برای نخستین بار بررسی کرد و نشان داد که هر منحنی یکتا نسبت ثابتی ( که بعدها به برون مرکزی معروف شد ) دارد و این نسبت ثابت برای هذلولی ها همیشه بیشتر از ۱ است. [ ۴]
نام آپولونیوس ( اواخر قرن سوم — اوایل قرن دوم پیش از میلاد ) برای قرن ها پس از مرگ او با مطالعهٔ مقاطع مخروطی گره خورده بود. آپولونیوس اثر مهمش «مخروطات» را، که مشتمل بر هشت مقاله است، [ ۵] با مطالعهٔ مخروط آغاز می کند و پس از تعریف سه مقطع مخروطی ( سهمی، هذلولی، و بیضی ) ، به تعریف خط مماس آن ها می پردازد و سپس ثابت می کند که فاصلهٔ کانونی برای همهٔ نقاط روی یک هذلولی ثابت است. [ ۶]
همزمان با حکومت مأمون در خراسان ( در قرن سوم هجری ) ، اخوان ثلاثهٔ بنوموسی دست به ترجمهٔ مخروطات آپولونیوس از یونانی به عربی زدند. بنوموسی فقط نسخه ای ناقص از مخروطات را در اختیار داشتند و مقاطع مخروطی در زمان ایشان به دست فراموشی سپرده شده بود، بنابراین در فهم متن دچار مشکل بودند. اندکی بعد، یکی از اخوان ثلاثه به نام حسن نظریهٔ مقاطع استوانه ای را ابداع کرد که می توان آن را مقدمه ای ساده بر مقاطع مخروطی دانست. پس از درگذشت حسن، برادرش احمد در شام نسخه ای کامل تر از چهار فصل اول مخروطات را با شرح اوتوکیوس پیدا کرد و به کمک برادر دیگرش، محمد، و با استفاده از دو نسخهٔ موجود و نظریهٔ حسن، موفق شد نظریات آپولونیوس را دریابد. احمد و محمد ترجمهٔ مقالهٔ اول تا چهارم مخروطات را به هلال حمصی و مقالهٔ پنجم تا هفتم آن را به ثابت بن قره سپردند و خود بازنگری نهایی ترجمه را عهده دار شدند. ترجمهٔ برادران بنوموسی از مقالات پنجم تا هفتم مخروطات تنها نسخهٔ باقی ماندهٔ این اثر است. [ ۵] ترجمهٔ آثار علمی به عربی اغلب نیازمند ابداع اصطلاحات فنی تازه بود و مترجمان آن ها، بر خلاف مترجمان لاتین، به ترانویسی عبارات یونانی اکتفا نکردند[ ب] و برای واژهٔ «اوپربول» اصطلاح «قطع زائد» را در نظر گرفتند که معنای آن را حفظ می کند[ پ] و هنوز در زبان عربی به هذلولی «قطع زائد» گفته می شود. [ ۵]

هُذْلولی (hyperbola)
هُذْلولی
در هندسه، منحنی حاصل از تقاطع یک سطح مخروطی دوار یا مخروط مستدیر قائم دو دامنه، با صفحه ای موازی با دو مولد از سطح دوار، که هر دو دامنۀ سطح را قطع می کند. هذلولی دو شاخه دارد و به دو مجانب محدود است. مجانب ها خط های راستی اند که شاخه های هذلولی به آن ها نزدیک و نزدیک تر می شوند، ولی هیچ گاه به آن ها نمی رسند. هذلولی ای با دو مجانب عمود برهم هذلولی متساوی الساقین، قائم یا متساوی القطرین نامیده می شود. مثلاً نمودار(فرمول ۱) هذلولی متساوی الساقینی است که محورهای مختصات مجانب های آن اند.فرمول ۱:هذلولی عضو خانوادۀ مقاطع مخروطی است. این منحنی را همچنین می توان به صورت مسیر حرکت نقطه ای تعریف کرد که تفاضل فواصلش از دو نقطۀ ثابت (کانونها) همواره ثابت باشد. اگر کانون ها را F و َF بنامیم، خط گذرنده از َFF یکی از محورهای تقارنهذلولی است و نقاط تقاطع آن را با دو شاخۀ هذلولی رأس های هذلولی می نامند. عمود منصف َFF محور تقارن دیگر است. محورهای تقارن هذلولی را محورهای آن می نامند. خروج از مرکز هذلولی بزرگ تر از یک است.