نگاشت (ریاضیات). نگاشت[ ۱] ( به انگلیسی: map ) در ریاضیات، به معنی ارتباطی است که میان اشیاء یا ساختارهای ریاضیاتی برقرار است. نگاشت ها می توانند پیکان یا تابع باشند هرچند که این مفاهیم در جاهایی همپوشانی دارند. در تابع ها، نگاشت می تواند دربارهٔ ساختارها بویژه دامنه مشترک مطرح شود. [ ۲] در نظریه رسته ها، از پیکان ها برای توصیف نگاشت استفاده می شود. نگاشت در منطق، علوم کامپیوتر و نظریه گرافها هم کاربرد دارد اما چندان فراگیر نیست.
در بسیاری از شاخه های ریاضی از عبارت نگاشت برای تعریف یک تابع استفاده می شود که گاهی این تابع ها ویژگی های خاصی دارند که در آن شاخهٔ ریاضی بسیار بااهمیت است برای نمونه در توپولوژی نگاشت یک تابع پیوسته است و در جبر خطی، نگاشت یک تغییرشکل خطی است و …
برخی نوسندگان کتاب های ریاضی مانند سرج لانگ، از عبارت تابع تنها برای اشاره به نگاشت هایی که در آنها دامنه مشترک مجموعه ای از اعداد است ( مانند R یا C )
برخی از نگاشت ها از اهمیت ویژه ای برخوردارند برای نمونه می توان به گروه لی، Mapping class group و Permutation group اشاره کرد.
عبارت هایی مانند دامنه، دامنه مشترک، یک به یک و پیوسته را هم می توان برای تابع و هم برای نگاشت استفاده کرد چون مفهوم مشترک دارند.
در نظریه رسته ها عبارت نگاشت معمولاً به عنوان معادل مورفیزم یا «پیکان» استفاده می شود بنابراین از «تابع»، عمومی تر است.
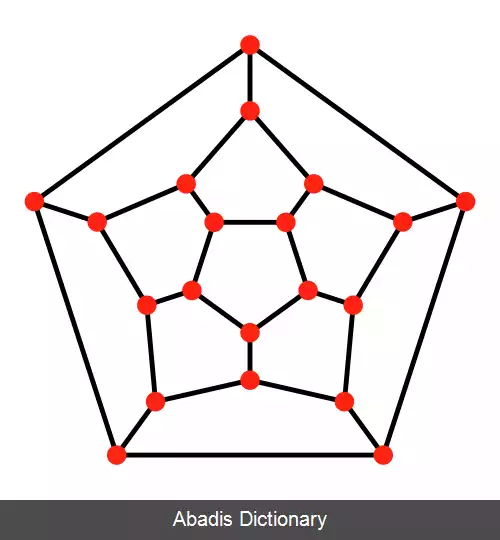
در نظریه گراف، نگاشت به معنی کشیدن یک گراف بر روی یک صفحه است بدون آنکه همپوشانی در ضلع هایش بوجود آید ( برازش گراف ) اگر صفحه مسطح باشد در آن صورت، نگاشت یک گراف مسطح است همین مطلب برای نقشه های زمین هم برقرار است. [ ۳]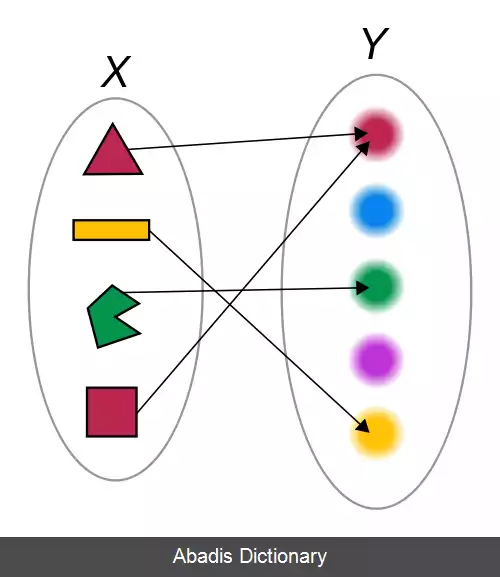
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر بسیاری از شاخه های ریاضی از عبارت نگاشت برای تعریف یک تابع استفاده می شود که گاهی این تابع ها ویژگی های خاصی دارند که در آن شاخهٔ ریاضی بسیار بااهمیت است برای نمونه در توپولوژی نگاشت یک تابع پیوسته است و در جبر خطی، نگاشت یک تغییرشکل خطی است و …
برخی نوسندگان کتاب های ریاضی مانند سرج لانگ، از عبارت تابع تنها برای اشاره به نگاشت هایی که در آنها دامنه مشترک مجموعه ای از اعداد است ( مانند R یا C )
برخی از نگاشت ها از اهمیت ویژه ای برخوردارند برای نمونه می توان به گروه لی، Mapping class group و Permutation group اشاره کرد.
عبارت هایی مانند دامنه، دامنه مشترک، یک به یک و پیوسته را هم می توان برای تابع و هم برای نگاشت استفاده کرد چون مفهوم مشترک دارند.
در نظریه رسته ها عبارت نگاشت معمولاً به عنوان معادل مورفیزم یا «پیکان» استفاده می شود بنابراین از «تابع»، عمومی تر است.
در نظریه گراف، نگاشت به معنی کشیدن یک گراف بر روی یک صفحه است بدون آنکه همپوشانی در ضلع هایش بوجود آید ( برازش گراف ) اگر صفحه مسطح باشد در آن صورت، نگاشت یک گراف مسطح است همین مطلب برای نقشه های زمین هم برقرار است. [ ۳]


wiki: نگاشت (ریاضیات)
