صفت نقطه گون ( به انگلیسی: pointwise ) در ریاضیات برای نمایش آن است که یک «ویژگی معین» توسط «سنجش هر مقدار f ( x ) برای تابع f » تعریف می شود. کلاس مهمی از مفاهیم نقطه گون همان عملیات نقطه گون است، یعنی، عملیاتی که روی توابع با اعمال عمل روی مقادیر تابع، به صورت مجزا، برای هر نقطه در دامنه تعریف می گردد. تعریف های نقطه گون درباره «روابط» هم به کار می رود.
می توان یک عمل دودویی o: Y × Y → Y روی مجموعه Y را به صورت نقطه گون به یک عمل O: ( X→Y ) × ( X→Y ) → ( X→Y ) روی مجموعه X→Y از همه توابع از X به Y به این شیوه ترفیع داد که: اگر دو تابع f1: X → Y و f2: X → Y داشته باشیم، تابع O ( f1, f2 ) : X → Y را به صورت زیر تعریف می کنیم:
معمولا o و O با نماد مشابهی نمایش داده می شوند. تعریف مشابهی برای عمل یکتایی o، و همچنین برای عمل هایی با آریتی دیگر به کار می رود. [ نیازمند منبع]
که در آن f , g : X → R است.
ضرب نقطه گون و نرده ای را ببینید.
یک مثال از عمل روی تابع که نقطه گون نیست، عمل هم گشت ( یا کانولوشن ) است.
عمل های نقطه گون وبژگی هایی مثل خاصیت انجمنی، جابجایی و توزیع پذیری را از عمل متناظر روی هم دامنه به ارث می برند. اگر A یک ساختار جبری باشد، مجموعه همه توابع X به مجموعه حامل A را می توان به یک ساختار جبری با نوع مشابه به روش مشابهی تبدیل نمود.
عمل های مولفه گون ( به انگلیسی: componentwise operations ) معمولا روی بردارها تعریف می شود، که در آن بردارها عناصر مجموعه K n هستند ( برای یک عدد طبیعی n و یک میدان K ) . اگر ما مولفه i ام از هر بردار v را به صورت v i نشان دهیم، آنوقت جمع مولفه گون برابر ( u + v ) i = u i + v i است.
عمل های مولفه گون را می توان روی ماتریس ها هم تعریف کرد. جمع ماتریسی، که در آن ( A + B ) i j = A i j + B i j است یک عمل مولفه گون است درحالیکه ضرب ماتریسی اینطور نیست.
یک تاپل را می توان نوعی تابع درنظر گرفت، و یک بردار یک تاپل است. از این رو، هر بردار v با تابع f : n → K متناظر است به این صورت که f ( i ) = v i و هر عمل مولفه گون روی بردارها برابر عمل نقطه گون روی توابع متناظر با آن بردارها هستند.
در نظریه ترتیب می توان ترتیب جزیی نقطه گون را روی توابع تعریف کرد. اگر A و B پوست باشند، می توان مجموعه توابع A → B را توسط f ≤ g مرتب نمود، اگر و فقط اگر ( ∀x ∈ A ) f ( x ) ≤ g ( x ) باشد. ترتیب های نقطه گون بعضی از ویژگی های پوست های مبنا را به ارث می برند. برای مثال اگر A و B مشبکه پیوسته باشند، آنوقت مجموعه توابع A → B هم با ترتیب نقطه گون، یک مشبکه پیوسته است. [ ۱] به کمک ترتیب نقطه گون روی توابع، می توان دیگر مفاهیم مهم دیگر را به دقت تعریف کرد، مثلا:[ ۲]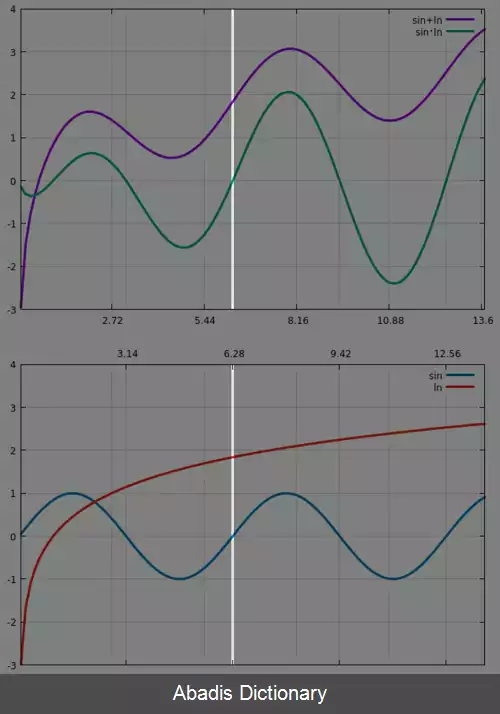
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمی توان یک عمل دودویی o: Y × Y → Y روی مجموعه Y را به صورت نقطه گون به یک عمل O: ( X→Y ) × ( X→Y ) → ( X→Y ) روی مجموعه X→Y از همه توابع از X به Y به این شیوه ترفیع داد که: اگر دو تابع f1: X → Y و f2: X → Y داشته باشیم، تابع O ( f1, f2 ) : X → Y را به صورت زیر تعریف می کنیم:
معمولا o و O با نماد مشابهی نمایش داده می شوند. تعریف مشابهی برای عمل یکتایی o، و همچنین برای عمل هایی با آریتی دیگر به کار می رود. [ نیازمند منبع]
که در آن f , g : X → R است.
ضرب نقطه گون و نرده ای را ببینید.
یک مثال از عمل روی تابع که نقطه گون نیست، عمل هم گشت ( یا کانولوشن ) است.
عمل های نقطه گون وبژگی هایی مثل خاصیت انجمنی، جابجایی و توزیع پذیری را از عمل متناظر روی هم دامنه به ارث می برند. اگر A یک ساختار جبری باشد، مجموعه همه توابع X به مجموعه حامل A را می توان به یک ساختار جبری با نوع مشابه به روش مشابهی تبدیل نمود.
عمل های مولفه گون ( به انگلیسی: componentwise operations ) معمولا روی بردارها تعریف می شود، که در آن بردارها عناصر مجموعه K n هستند ( برای یک عدد طبیعی n و یک میدان K ) . اگر ما مولفه i ام از هر بردار v را به صورت v i نشان دهیم، آنوقت جمع مولفه گون برابر ( u + v ) i = u i + v i است.
عمل های مولفه گون را می توان روی ماتریس ها هم تعریف کرد. جمع ماتریسی، که در آن ( A + B ) i j = A i j + B i j است یک عمل مولفه گون است درحالیکه ضرب ماتریسی اینطور نیست.
یک تاپل را می توان نوعی تابع درنظر گرفت، و یک بردار یک تاپل است. از این رو، هر بردار v با تابع f : n → K متناظر است به این صورت که f ( i ) = v i و هر عمل مولفه گون روی بردارها برابر عمل نقطه گون روی توابع متناظر با آن بردارها هستند.
در نظریه ترتیب می توان ترتیب جزیی نقطه گون را روی توابع تعریف کرد. اگر A و B پوست باشند، می توان مجموعه توابع A → B را توسط f ≤ g مرتب نمود، اگر و فقط اگر ( ∀x ∈ A ) f ( x ) ≤ g ( x ) باشد. ترتیب های نقطه گون بعضی از ویژگی های پوست های مبنا را به ارث می برند. برای مثال اگر A و B مشبکه پیوسته باشند، آنوقت مجموعه توابع A → B هم با ترتیب نقطه گون، یک مشبکه پیوسته است. [ ۱] به کمک ترتیب نقطه گون روی توابع، می توان دیگر مفاهیم مهم دیگر را به دقت تعریف کرد، مثلا:[ ۲]

wiki: نقطه گون
