مقطع مخروطی ( به انگلیسی: Conic section ) ، به خمی گویند که از برخورد یک مخروط و یک صفحه حاصل شود.
اثبات اینکه در حالت غیر انحطاط این منحنی ها، که به عنوان منحنی های مکان در صفحه تعریف می شوند، واقعاً به وجود می آیند، می تواند بدون محاسبه با کمک کره های دندلین انجام شود. اثبات ریاضی در اینجا در مقاطع صفحه بخش مخروط واحد آورده شده است. یک مخروط همچنین می تواند به عنوان یک مورد خاص دو بعدی از یک چهارگانه دیده شود و می توان آن را با یک معادله درجه دوم، معادله مخروطی عمومی توصیف کرد. جاسازی یک بیضی، هذلولی و سهمی در یک صفحه نمایشی منجر به مخروط های تصویری می شود که همگی معادل یکدیگر هستند، یعنی؛ یعنی می توان آنها را با نگاشت خط مستقیم به یکدیگر تبدیل کرد.
معادلهٔ یک مقطع مخروطی به صورت معادلهٔ درجه دو زیر برحسب x , y بیان می شود:[ ۱]
a x 2 + 2 h x y + b y 2 + 2 g x + 2 f y + c = 0
برای تعیین اینکه منحنی ها/نقاطی که در بالا به عنوان مقاطع مخروطی به آنها اشاره شد در واقع زمانی رخ می دهند که یک مخروط یک صفحه را قطع می کند، در اینجا مخروط واحد را قطع می کنیم ( مستقیم مخروط دایره ای ) K 1 : x 2 + y 2 = z 2 با صفحه موازی با محور y. این یک محدودیت نیست زیرا مخروط به صورت چرخشی متقارن است. هر مخروط دایره ای سمت راست، تصویر پیوندی مخروط واحد K 1 است و بیضی ها/hyperbolas/parabolas/. . . با یک نقشه برداری affine به همان شکل برگردید. داده شده: صفحه ε : a x + c z = d , مخروط K 1 : x 2 + y 2 = z 2 . جستجو: تقاطع ε ∩ K 1 .
• Fall I: c = 0 {\displaystyle c=0} In diesem Fall ist die Ebene senkrecht und a ≠ 0 {\displaystyle a\neq 0} und x = d / a {\displaystyle x=d/a} . Eliminiert man x {\displaystyle x} aus der Kegelgleichung, so erhält man z 2 − y 2 = d 2 / a 2 {\displaystyle z^{2} - y^{2}=d^{2}/a^{2}} .
• Fall Ia: d = 0 {\displaystyle d=0} . In diesem Fall besteht der Schnitt aus dem Geradenpaar t ( 0 , 1 , ± 1 ) , t ∈ R . {\displaystyle t ( 0, 1, \pm 1 ) , \ t\in \mathbb {R} . } .
• Fall Ib: d ≠ 0 {\displaystyle d\neq 0} . Die obige Gleichung beschreibt jetzt eine Hyperbel in der y - z - Ebene. Also ist auch die Schnittkurve ε ∩ K 1 {\displaystyle \varepsilon \cap K_{1}} selbst eine Hyperbel.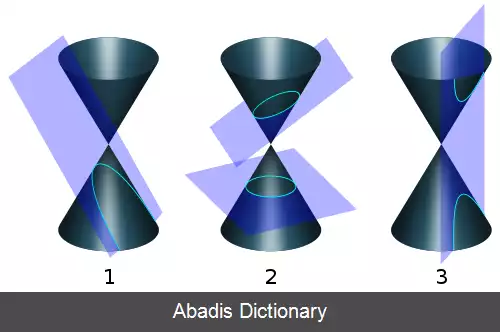
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاثبات اینکه در حالت غیر انحطاط این منحنی ها، که به عنوان منحنی های مکان در صفحه تعریف می شوند، واقعاً به وجود می آیند، می تواند بدون محاسبه با کمک کره های دندلین انجام شود. اثبات ریاضی در اینجا در مقاطع صفحه بخش مخروط واحد آورده شده است. یک مخروط همچنین می تواند به عنوان یک مورد خاص دو بعدی از یک چهارگانه دیده شود و می توان آن را با یک معادله درجه دوم، معادله مخروطی عمومی توصیف کرد. جاسازی یک بیضی، هذلولی و سهمی در یک صفحه نمایشی منجر به مخروط های تصویری می شود که همگی معادل یکدیگر هستند، یعنی؛ یعنی می توان آنها را با نگاشت خط مستقیم به یکدیگر تبدیل کرد.
معادلهٔ یک مقطع مخروطی به صورت معادلهٔ درجه دو زیر برحسب x , y بیان می شود:[ ۱]
a x 2 + 2 h x y + b y 2 + 2 g x + 2 f y + c = 0
برای تعیین اینکه منحنی ها/نقاطی که در بالا به عنوان مقاطع مخروطی به آنها اشاره شد در واقع زمانی رخ می دهند که یک مخروط یک صفحه را قطع می کند، در اینجا مخروط واحد را قطع می کنیم ( مستقیم مخروط دایره ای ) K 1 : x 2 + y 2 = z 2 با صفحه موازی با محور y. این یک محدودیت نیست زیرا مخروط به صورت چرخشی متقارن است. هر مخروط دایره ای سمت راست، تصویر پیوندی مخروط واحد K 1 است و بیضی ها/hyperbolas/parabolas/. . . با یک نقشه برداری affine به همان شکل برگردید. داده شده: صفحه ε : a x + c z = d , مخروط K 1 : x 2 + y 2 = z 2 . جستجو: تقاطع ε ∩ K 1 .
• Fall I: c = 0 {\displaystyle c=0} In diesem Fall ist die Ebene senkrecht und a ≠ 0 {\displaystyle a\neq 0} und x = d / a {\displaystyle x=d/a} . Eliminiert man x {\displaystyle x} aus der Kegelgleichung, so erhält man z 2 − y 2 = d 2 / a 2 {\displaystyle z^{2} - y^{2}=d^{2}/a^{2}} .
• Fall Ia: d = 0 {\displaystyle d=0} . In diesem Fall besteht der Schnitt aus dem Geradenpaar t ( 0 , 1 , ± 1 ) , t ∈ R . {\displaystyle t ( 0, 1, \pm 1 ) , \ t\in \mathbb {R} . } .
• Fall Ib: d ≠ 0 {\displaystyle d\neq 0} . Die obige Gleichung beschreibt jetzt eine Hyperbel in der y - z - Ebene. Also ist auch die Schnittkurve ε ∩ K 1 {\displaystyle \varepsilon \cap K_{1}} selbst eine Hyperbel.


wiki: مقطع مخروطی
