مسئلهٔ کوچکترین دایره یا کمینه دایره پوششی نقاط، یک مسئله ریاضی است که کوچکترین دایره پوششی شامل همه نقاط صفحه اقلیدسی را محاسبه می کند. مسئله کوچکترین دایره پوششی در فضای n بعدی، مسئله ای است که کوچکترین کره که همه مجموعه نقاط را شامل می شود، محاسبه می کند. [ ۱] این مسئله در ابتدا توسط ریاضی دان انگلیسی James Joseph Sylvester در سال ۱۸۵۷ مطرح شد. [ ۲] مسئله کوچک ترین دایره در صفحه یک مثال از مسئله تحلیل تعیین محل است به طوری که محل یک امکان جدید باید به گونه ای انتخاب شود که دورترین فاصله ای که هر مشتری باید طی کند تا به این امکان برسد کمینه شود. [ ۳] مسئله پیدا کردن کوچک ترین دایره در صفحه در ابعاد بالاتر هم در زمان خطی قابل حل است.
اغلب روش های هندسی برای حل این مسئله، نقاطی را در نظر می گیرند که روی مرز کوچک ترین دایره واقع شده اند و برپایهٔ دو اصل سادهٔ زیر می باشند:
۱ ) کوچک ترین دایرهٔ پوششی نقاط یکتاست.
۲ ) کوچک ترین دایرهٔ پوششی برای مجموعهٔ نقاط S، حداکثر با ۳ نقطه از S روی مرز دایره مشخص می شود. اگر این دایره با دو نقطه مشخص شود، در این صورت خط متصل کنندهٔ این دو نقطه باید قطر کوچک ترین دایرهٔ پوششی نقاط باشد و اگر با سه نقطه مشخص گردد آنگاه مثلث شامل این سه نقطه منفرجه نخواهد بود.
همان طور که نیمورد مگیدو ( Nimrod Megiddo ) نشان داد، [ ۴] مسئلهٔ کوچک ترین دایره پوششی نقاط می تواند در زمان خطی حل شود و برای این مسئله در فضای اقلیدسی در هر بعد ثابتی همین زمان اجرا وجود دارد.
المو ولز ( Emo Welzl ) [ ۵] یک الگوریتم تصادفی برای کوچک ترین دایره پوششی نقاط با زمان اجرای ( O ( n ارائه داد که این الگوریتم بر پایهٔ الگوریتم برنامه خطی ریموند سیدل ( Raimund Seidel ) است. این الگوریتم بازگشتی، مجموعه نقاط Q و S را به عنوان آرگومان دریافت می کند و کوچک ترین دایرهٔ پوششی از اجتماع Q و S را تا زمانی که هر نقطه از Q نقطه ای از نقاط مرزی کوچک ترین دایره نهایی شود محاسبه می کند. بنابراین، برای حل مسئله اصلی می توانیم الگوریتم فوق را برای مجموعه S که شامل نقاطی که قرار است پوشش داده شوند و Q که یک مجموعه تهی است فراخوانی کرد. همان طور که الگوریتم به صورت بازگشتی فراخوانی می شود، مجموعه Q تا زمانی که مساوی همه نقاط مرزی دایره نشده است بزرگ می شود.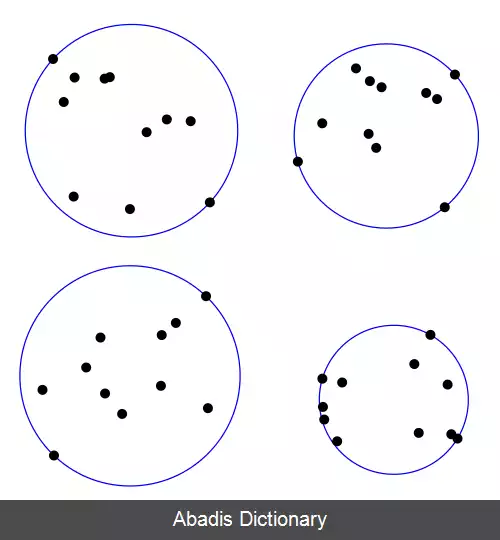

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاغلب روش های هندسی برای حل این مسئله، نقاطی را در نظر می گیرند که روی مرز کوچک ترین دایره واقع شده اند و برپایهٔ دو اصل سادهٔ زیر می باشند:
۱ ) کوچک ترین دایرهٔ پوششی نقاط یکتاست.
۲ ) کوچک ترین دایرهٔ پوششی برای مجموعهٔ نقاط S، حداکثر با ۳ نقطه از S روی مرز دایره مشخص می شود. اگر این دایره با دو نقطه مشخص شود، در این صورت خط متصل کنندهٔ این دو نقطه باید قطر کوچک ترین دایرهٔ پوششی نقاط باشد و اگر با سه نقطه مشخص گردد آنگاه مثلث شامل این سه نقطه منفرجه نخواهد بود.
همان طور که نیمورد مگیدو ( Nimrod Megiddo ) نشان داد، [ ۴] مسئلهٔ کوچک ترین دایره پوششی نقاط می تواند در زمان خطی حل شود و برای این مسئله در فضای اقلیدسی در هر بعد ثابتی همین زمان اجرا وجود دارد.
المو ولز ( Emo Welzl ) [ ۵] یک الگوریتم تصادفی برای کوچک ترین دایره پوششی نقاط با زمان اجرای ( O ( n ارائه داد که این الگوریتم بر پایهٔ الگوریتم برنامه خطی ریموند سیدل ( Raimund Seidel ) است. این الگوریتم بازگشتی، مجموعه نقاط Q و S را به عنوان آرگومان دریافت می کند و کوچک ترین دایرهٔ پوششی از اجتماع Q و S را تا زمانی که هر نقطه از Q نقطه ای از نقاط مرزی کوچک ترین دایره نهایی شود محاسبه می کند. بنابراین، برای حل مسئله اصلی می توانیم الگوریتم فوق را برای مجموعه S که شامل نقاطی که قرار است پوشش داده شوند و Q که یک مجموعه تهی است فراخوانی کرد. همان طور که الگوریتم به صورت بازگشتی فراخوانی می شود، مجموعه Q تا زمانی که مساوی همه نقاط مرزی دایره نشده است بزرگ می شود.


wiki: مسئله کوچک ترین دایره
