فرهنگ فارسی
فرهنگ معین
فرهنگ عمید
۲. (ریاضی ) آرایۀ مستطیل شکل از کمیت های جبری یا اعداد که در داخل دو کروشه و به صورت ستون های منظم نوشته می شوند و به وسیلۀ آن عملیات ریاضی انجام می شود.
فرهنگستان زبان و ادب
دانشنامه عمومی
ماتریس ( به فرانسوی: Matrice ) و ( به انگلیسی: Matrix ) به آرایشی مستطیلی شکل از اعداد یا عبارات ریاضی که به صورت سطر و ستون شکل یافته گفته می شود. به طوری که می توان گفت که هر ستون یا هر سطر یک ماتریس، یک بردار را تشکیل می دهد. هر یک از عناصر ماتریس دِرایه خوانده می شود.
ماتریسی با ۲ سطر و ۳ ستون به این شکل است.
ماتریس های هم اندازه ( با تعداد سطر و ستون برابر ) را می توان با هم جمع یا از هم تفریق کرد. ضرب دو ماتریس تنها در صورتی ممکن است که تعداد ستون های ماتریس نخست با تعداد سطرهای ماتریس دوم برابر باشد.
در جبر خطی، می توان اثبات کرد که هر نگاشت خطیِ، از فضای R n به فضای R m ، یک ریخت با یک ماتریس m × n ( m سطر و n ستون ) می باشد. ماتریس ها کاربردهای فراوانی در جبر خطی دارند.
یکی از کاربردهای ماتریس ها در حل دستگاه معادلات خطی ست. اگر ماتریس مربعی باشد، برخی مشخصات آن را می توان از دترمینان آن دریافت. برای نمونه یک ماتریس مربعی معکوس پذیر است اگر و تنها اگر دترمینان آن ناصفر باشد. مقدار ویژه و بردار ویژه اطلاعاتی دربارهٔ هندسهٔ نگاشت های خطی می دهند.
ماتریس ها در بیشتر زمینه های دانش کاربرد دارند. در تمامی شاخه های فیزیک، شامل مکانیک کلاسیک، نورشناسی، الکترومغناطیس، مکانیک کوانتوم و الکترودینامیک کوانتومی ماتریس برای مطالعهٔ پدیده های فیزیکی شاخه مورد نظر به کار می رود.
به هر یک از عناصر که درون ماتریس می آیند دَرآیه یا دَرایه می گویند. در صورتی که مقدار یک درایه مشخص نباشد، برای مشخص کردن هر درایه عدد ردیف و ستون آن را به صورت پایین نویس حرف کوچک نام ماتریس نوشته می شود. [ ۱] برای نمونه اگر نام ماتریسی A باشد، درایه ای که در ردیف نخست و ستون دوم قرار دارد نوشته می شود a۱۲ و خوانده می شود «درایهٔ یک دو». درایه های یک ماتریس در حالت کلی می توانند حقیقی یا مختلط و یا هر چیز دیگری مانند چند جمله ای، یا تابعی خاص و یا خود یک ماتریس دیگر و. . . باشد.
ابعاد یک ماتریس با تعداد سطر و ستون آن تعیین می شود. ابعاد ماتریسی با m سطر و n ستون به صورت m × n نوشته و m در n خوانده می شود. برای نمونه ابعاد ماتریس A سه در دو ( ۲×۳ ) است.
ماتریسی که تنها یک سطر دارد بردار سطری و ماتریسی که تنها یک ستون دارد بردار ستونی نامیده می شود. ماتریسی که تعداد سطر و ستون برابر دارد ماتریس مربعی نامیده می شود. ماتریسی با تعداد سطر یا ستون ( یا هر دو ) بی نهایت ماتریس بی نهایت خوانده می شود. ماتریس تهی ماتریسی ست که سطر و ستونی ندارد.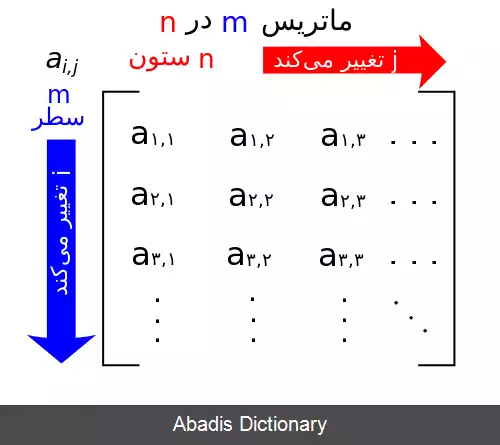
ماتریسی با ۲ سطر و ۳ ستون به این شکل است.
ماتریس های هم اندازه ( با تعداد سطر و ستون برابر ) را می توان با هم جمع یا از هم تفریق کرد. ضرب دو ماتریس تنها در صورتی ممکن است که تعداد ستون های ماتریس نخست با تعداد سطرهای ماتریس دوم برابر باشد.
در جبر خطی، می توان اثبات کرد که هر نگاشت خطیِ، از فضای R n به فضای R m ، یک ریخت با یک ماتریس m × n ( m سطر و n ستون ) می باشد. ماتریس ها کاربردهای فراوانی در جبر خطی دارند.
یکی از کاربردهای ماتریس ها در حل دستگاه معادلات خطی ست. اگر ماتریس مربعی باشد، برخی مشخصات آن را می توان از دترمینان آن دریافت. برای نمونه یک ماتریس مربعی معکوس پذیر است اگر و تنها اگر دترمینان آن ناصفر باشد. مقدار ویژه و بردار ویژه اطلاعاتی دربارهٔ هندسهٔ نگاشت های خطی می دهند.
ماتریس ها در بیشتر زمینه های دانش کاربرد دارند. در تمامی شاخه های فیزیک، شامل مکانیک کلاسیک، نورشناسی، الکترومغناطیس، مکانیک کوانتوم و الکترودینامیک کوانتومی ماتریس برای مطالعهٔ پدیده های فیزیکی شاخه مورد نظر به کار می رود.
به هر یک از عناصر که درون ماتریس می آیند دَرآیه یا دَرایه می گویند. در صورتی که مقدار یک درایه مشخص نباشد، برای مشخص کردن هر درایه عدد ردیف و ستون آن را به صورت پایین نویس حرف کوچک نام ماتریس نوشته می شود. [ ۱] برای نمونه اگر نام ماتریسی A باشد، درایه ای که در ردیف نخست و ستون دوم قرار دارد نوشته می شود a۱۲ و خوانده می شود «درایهٔ یک دو». درایه های یک ماتریس در حالت کلی می توانند حقیقی یا مختلط و یا هر چیز دیگری مانند چند جمله ای، یا تابعی خاص و یا خود یک ماتریس دیگر و. . . باشد.
ابعاد یک ماتریس با تعداد سطر و ستون آن تعیین می شود. ابعاد ماتریسی با m سطر و n ستون به صورت m × n نوشته و m در n خوانده می شود. برای نمونه ابعاد ماتریس A سه در دو ( ۲×۳ ) است.
ماتریسی که تنها یک سطر دارد بردار سطری و ماتریسی که تنها یک ستون دارد بردار ستونی نامیده می شود. ماتریسی که تعداد سطر و ستون برابر دارد ماتریس مربعی نامیده می شود. ماتریسی با تعداد سطر یا ستون ( یا هر دو ) بی نهایت ماتریس بی نهایت خوانده می شود. ماتریس تهی ماتریسی ست که سطر و ستونی ندارد.

wiki: ماتریس
ماتریس (شیوه نامه). ماتریس ( به انگلیسی: Matrix ) یک شیوه نامهٔ استاندارد و سبک وزن باز برای برقراری ارتباط بی درنگ است. این شیوه نامه برای این طراحی شده است که به کاربران دارای حساب در یک رساننده خدمات ارتباطی امکان برقراری ارتباط با کاربران دیگر رساننده های خدمات ارتباطی را از طریق گفتگوی اینترنتی، صدا روی پرتکل اینترنت و خدمات تلفن تصویری فراهم کند. هدف این است که ارتباطات بی درنگ یکپارچه بین ارائه دهندگان خدمات مختلف کار کند، دقیقاً مانند همان کاری که شیوه نامهٔ سادهٔ نامه رسانی اکنون برای خدمت ذخیره و ارسال رایانامه انجام می دهد.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف
wiki: ماتریس (شیوه نامه)
دانشنامه آزاد فارسی
ماتْریس (matrix)
ماتْریس
در ریاضیات، آرایهای مستطیلی، شامل m سطر و n ستون، یا مربعی شامل n سطر و n ستون، از اعداد یا عبارت های جبری. این اعداد و عبارات عناصر یا درایه های ماتریس نامیده می شوند. ماتریس برای تسهیلِ بررسی مسائلی به کار می رود که در آن ها رابطۀ بین این عناصر مهم است. در واقع، ماتریس وسیله ای برای فشرده سازی اطلاعات دستگاه های ریاضی است و در موارد متعدد، ازجمله برای حل دستگاه های معادلات خطی (← دستگاه معادلات)، به کار می رود. فایدۀ ماتریس در این است که به جای درنظرگرفتن تعدادی کمیت جداجدا، به آرایشی از همۀ آن ها یک نماد نسبت داده و آن را از نظر جبری مطالعه می کنند. این نماد معمولاً یکی از حروف بزرگ الفبای لاتین است و درایه های ماتریس را هم معمولاً با حرف کوچک متناظر، همراه با زیرنویس های نشان دهندۀ سطر و ستون درایه، نشان می دهند. مثلاً ، ماتریس را با Aو درایه های آن را aij می نمایانند که به معنیِ درایۀ واقع در سطر i ام و ستون j ام است. ماتریس را نیز گاه با نشان می دهند. اندازه یا مرتبه ماتریس برحسب تعداد سطرها و ستون های آن بیان می شود، مثلاً ماتریسی که سه سطر و دو ستون دارد، ماتریسی ۲×۳ است. به طور کلی، ماتریسی با m سطر و n ستون را ماتریس m×n می گویند. ماتریسی که تعداد سطرها و ستون هایش برابر باشد، ماتریس مربعی نامیده می شود و مرتبۀ آن تعداد سطرها یا ستون هایش است. به هر ماتریس مربعی عددی به نام دترمینان نسبت می دهند. دو ماتریس A و B را برابر گویند، اگر تعداد سطرهای شان باهم و تعداد ستون های شان باهم برابر و به ازای هر i و هر j تساوی aij = bij برقرار باشد. مجموع دو ماتریس A و B، که هر دو m×n باشند، ماتریسی m×n چون S=A+B است که هر درایۀ sijواقع در سطر i ام و ستون j ام آن، برابر aij + bij، یعنی مجموع درایه های A و B در سطر و ستون متناظر، است. حاصل ضرب اسکالر عدد c در ماتریس A ماتریسی است که با cA یا Ac نشان داده می شود و درایه های آن عبارت اند از caij. برای ضرب ماتریس ها باید تعداد ستون های ماتریس اول با تعداد سطرهای ماتریس دوم برابر باشد. حاصل ضرب ماتریس A در ماتریس B ماتریسی است مانند C که تعداد سطرهایش برابر تعداد سطرهای A و تعداد ستون هایش برابر تعداد ستون های B است، یعنی اگر A ماتریسی m×n و B ماتریسی n×p باشد، C ماتریسی m×p است. درایۀ cijواقع در سطر i ام و ستون j ام C به این طریق به دست می آید که درایۀ اول سطر i ام A در درایۀ اول ستون j ام B، درایۀ دوم سطر i ام A در درایۀ دوم ستون j ام B، و به همین ترتیب، ضرب می شود و حاصل ضرب ها را با هم جمع می کنند یعنی cij = ai۱ b۱j + ai۲b۲j + .... + ain bnj. نظریۀ اولیۀ ماتریس را عمدتاً آرتور کیلی (۱۸۲۱ـ ۱۸۹۵)، ریاضی دان بریتانیایی، ابداع کرد، ولی واضع اصطلاح ماتریس ریاضی دان معاصر کیلی، جیمز سیلوستر (۱۸۱۴ـ ۱۸۹۷)، بود.
ماتْریس
در ریاضیات، آرایهای مستطیلی، شامل m سطر و n ستون، یا مربعی شامل n سطر و n ستون، از اعداد یا عبارت های جبری. این اعداد و عبارات عناصر یا درایه های ماتریس نامیده می شوند. ماتریس برای تسهیلِ بررسی مسائلی به کار می رود که در آن ها رابطۀ بین این عناصر مهم است. در واقع، ماتریس وسیله ای برای فشرده سازی اطلاعات دستگاه های ریاضی است و در موارد متعدد، ازجمله برای حل دستگاه های معادلات خطی (← دستگاه معادلات)، به کار می رود. فایدۀ ماتریس در این است که به جای درنظرگرفتن تعدادی کمیت جداجدا، به آرایشی از همۀ آن ها یک نماد نسبت داده و آن را از نظر جبری مطالعه می کنند. این نماد معمولاً یکی از حروف بزرگ الفبای لاتین است و درایه های ماتریس را هم معمولاً با حرف کوچک متناظر، همراه با زیرنویس های نشان دهندۀ سطر و ستون درایه، نشان می دهند. مثلاً ، ماتریس را با Aو درایه های آن را aij می نمایانند که به معنیِ درایۀ واقع در سطر i ام و ستون j ام است. ماتریس را نیز گاه با نشان می دهند. اندازه یا مرتبه ماتریس برحسب تعداد سطرها و ستون های آن بیان می شود، مثلاً ماتریسی که سه سطر و دو ستون دارد، ماتریسی ۲×۳ است. به طور کلی، ماتریسی با m سطر و n ستون را ماتریس m×n می گویند. ماتریسی که تعداد سطرها و ستون هایش برابر باشد، ماتریس مربعی نامیده می شود و مرتبۀ آن تعداد سطرها یا ستون هایش است. به هر ماتریس مربعی عددی به نام دترمینان نسبت می دهند. دو ماتریس A و B را برابر گویند، اگر تعداد سطرهای شان باهم و تعداد ستون های شان باهم برابر و به ازای هر i و هر j تساوی aij = bij برقرار باشد. مجموع دو ماتریس A و B، که هر دو m×n باشند، ماتریسی m×n چون S=A+B است که هر درایۀ sijواقع در سطر i ام و ستون j ام آن، برابر aij + bij، یعنی مجموع درایه های A و B در سطر و ستون متناظر، است. حاصل ضرب اسکالر عدد c در ماتریس A ماتریسی است که با cA یا Ac نشان داده می شود و درایه های آن عبارت اند از caij. برای ضرب ماتریس ها باید تعداد ستون های ماتریس اول با تعداد سطرهای ماتریس دوم برابر باشد. حاصل ضرب ماتریس A در ماتریس B ماتریسی است مانند C که تعداد سطرهایش برابر تعداد سطرهای A و تعداد ستون هایش برابر تعداد ستون های B است، یعنی اگر A ماتریسی m×n و B ماتریسی n×p باشد، C ماتریسی m×p است. درایۀ cijواقع در سطر i ام و ستون j ام C به این طریق به دست می آید که درایۀ اول سطر i ام A در درایۀ اول ستون j ام B، درایۀ دوم سطر i ام A در درایۀ دوم ستون j ام B، و به همین ترتیب، ضرب می شود و حاصل ضرب ها را با هم جمع می کنند یعنی cij = ai۱ b۱j + ai۲b۲j + .... + ain bnj. نظریۀ اولیۀ ماتریس را عمدتاً آرتور کیلی (۱۸۲۱ـ ۱۸۹۵)، ریاضی دان بریتانیایی، ابداع کرد، ولی واضع اصطلاح ماتریس ریاضی دان معاصر کیلی، جیمز سیلوستر (۱۸۱۴ـ ۱۸۹۷)، بود.
wikijoo: ماتریس
مترادف ها
موطن، رحم، ماتریس، زهدان، بچه دان، جای پیدایش
پیشنهاد کاربران
ماتریس: این نام در سنسکریت ماترِس mātres ( مادران آسمانی یا انرژی های خدایی که در پیکر مادران نمود یافته است ) می باشد.
مجموعه ای از درایه هاتشکیل شده از از سطر و ستون
که انواعی دارد
قطری
مربعی
بالا مثلثی
پایین مثلثی
اسکالر
صفر
همیوغ
نامتقارن
متعامد
سطری
ستونی
که انواعی دارد
قطری
مربعی
بالا مثلثی
پایین مثلثی
اسکالر
صفر
همیوغ
نامتقارن
متعامد
سطری
ستونی
قالب ریخته گری
قالب صنعتی
قالب ، زمینه ، شبکه ، زهدان ، رحم ، بچه دان ، موطن ، جاى پیدایش ، ماتریس
( اسم ) قالب مخصوص حروف سربی در چاپخانه
