در ریاضیات، قضیهٔ فیثاغوریس یک رابطهٔ بنیادی هندسه اقلیدسی بین سه ضلع مثلث قائم الزاویه است. این قضیه بیان می کند که مساحت مربعی که ضلع اش وتر است ( سمت مقابل زاویه قائمه ) برابر با مجموع مساحت های مریع های روی دو ضلع دیگر می باشد.
این قضیه را می توان به صورت یک معادلهٔ بین طول های اضلاع a ، b و وتر c نوشت، که گاهی اوقات معادلهٔ فیثاغوریس نامیده می شود:[ ۱]
این قضیه به نام ریاضی دان یونانی فیثاغورس نامگذاری شده است.
وارون این قضیه نیز درست است، به عبارت دیگر، اگر باشد، مثلث قائم الزاویه است. اثبات عکس قضیه فیثاغورس را به اقلیدس نسبت داده اند. [ ۲] [ ۳]
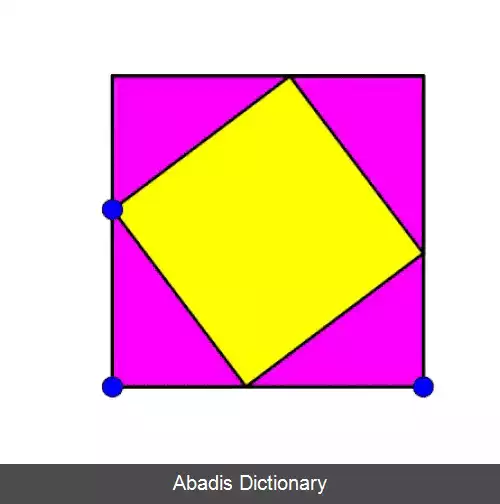
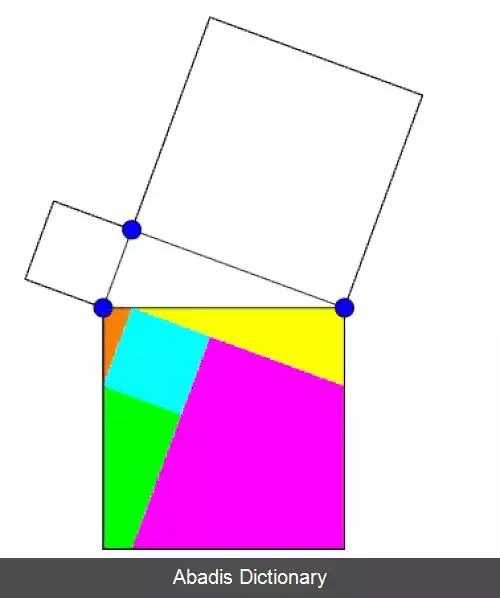
این قضیه بارها به روش های مختلف هندسی و جبری اثبات شده است که برخی از این اثبات ها به هزاران سال گذشته برمیگردند.
اگر c طول وتر مثلث راست گوشه باشد و a و b طول دو ضلع دیگر آن، قضیهٔ فیثاغورس را به شکل رابطهٔ زیر می نویسیم:
و اگر مقدار a و b معلوم باشد c را به این شکل بدست می آوریم:
و اگر c معلوم باشد و یکی از دو ضلع a یا b نامعلوم، آن ها را اینگونه بدست می آوریم:
یا
رابطه فیثاغورس به روش ساده ای اضلاع مثلث قائم الزاویه را به هم ربط می دهد، به طوریکه اگر طول دوضلع معلوم باشد طول ضلع سوم را می توان به دست آورد. پیامد دیگر این قضیه این است که در هر مثلث قائم الزاویه، طول وتر بیشتر از هر یک از دو ضلع دیگر، ولی کمتر از مجموع دو ضلع دیگر است.
یکی از تعمیم های قضیهٔ فیثاغورس قانون کسینوس ها ( قانون کاشانی ) است، [ ۴] که امکان محاسبهٔ طول هر یک از اضلاع هر نوع مثلثی را با داشتن دو ضلع دیگر و زاویهٔ بین آن دوضلع را می دهد. اگر زاویه بین دو ضلع دیگر قائمه باشد، قانون کسینوس ها تبدیل به قانون فیثاغورس می شود.
تمامی مثلثات فیثاغورس حالت خاصی از مثلت زیر می باشند که با جایگذاری اعداد مختلف می توان به بی نهایت مثلث دست پیدا کرد.
در این مثلث :
n ϵ R
r=4n+1
x=4n
y= 8 n + 1
با استفاده از فرمول های بالا و با جایگذاری تمامی اعداد حقیقی می توان به تمامی مثلثات فیثاغورسی دست یافت.
به عبارتی دیگر تمامی مثلثات طلایی حالت خاصی از این فرمول به ازای اعداد n=1 و n=3 هستند.
قضیهٔ فیثاغورس، قضیه ای است که بیش از هر قضیهٔ دیگری اثبات دارد، در کتاب قضیه فیثاغورس حدود ۳۷۰ اثبات برای این قضیه آورده شده است. [ ۵]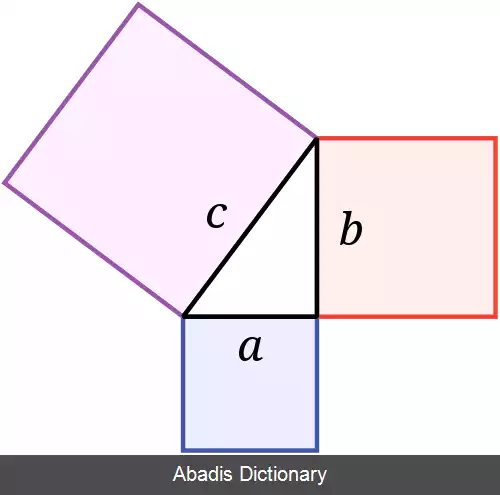

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین قضیه را می توان به صورت یک معادلهٔ بین طول های اضلاع a ، b و وتر c نوشت، که گاهی اوقات معادلهٔ فیثاغوریس نامیده می شود:[ ۱]
این قضیه به نام ریاضی دان یونانی فیثاغورس نامگذاری شده است.
وارون این قضیه نیز درست است، به عبارت دیگر، اگر باشد، مثلث قائم الزاویه است. اثبات عکس قضیه فیثاغورس را به اقلیدس نسبت داده اند. [ ۲] [ ۳]
این قضیه بارها به روش های مختلف هندسی و جبری اثبات شده است که برخی از این اثبات ها به هزاران سال گذشته برمیگردند.
اگر c طول وتر مثلث راست گوشه باشد و a و b طول دو ضلع دیگر آن، قضیهٔ فیثاغورس را به شکل رابطهٔ زیر می نویسیم:
و اگر مقدار a و b معلوم باشد c را به این شکل بدست می آوریم:
و اگر c معلوم باشد و یکی از دو ضلع a یا b نامعلوم، آن ها را اینگونه بدست می آوریم:
یا
رابطه فیثاغورس به روش ساده ای اضلاع مثلث قائم الزاویه را به هم ربط می دهد، به طوریکه اگر طول دوضلع معلوم باشد طول ضلع سوم را می توان به دست آورد. پیامد دیگر این قضیه این است که در هر مثلث قائم الزاویه، طول وتر بیشتر از هر یک از دو ضلع دیگر، ولی کمتر از مجموع دو ضلع دیگر است.
یکی از تعمیم های قضیهٔ فیثاغورس قانون کسینوس ها ( قانون کاشانی ) است، [ ۴] که امکان محاسبهٔ طول هر یک از اضلاع هر نوع مثلثی را با داشتن دو ضلع دیگر و زاویهٔ بین آن دوضلع را می دهد. اگر زاویه بین دو ضلع دیگر قائمه باشد، قانون کسینوس ها تبدیل به قانون فیثاغورس می شود.
تمامی مثلثات فیثاغورس حالت خاصی از مثلت زیر می باشند که با جایگذاری اعداد مختلف می توان به بی نهایت مثلث دست پیدا کرد.
در این مثلث :
n ϵ R
r=4n+1
x=4n
y= 8 n + 1
با استفاده از فرمول های بالا و با جایگذاری تمامی اعداد حقیقی می توان به تمامی مثلثات فیثاغورسی دست یافت.
به عبارتی دیگر تمامی مثلثات طلایی حالت خاصی از این فرمول به ازای اعداد n=1 و n=3 هستند.
قضیهٔ فیثاغورس، قضیه ای است که بیش از هر قضیهٔ دیگری اثبات دارد، در کتاب قضیه فیثاغورس حدود ۳۷۰ اثبات برای این قضیه آورده شده است. [ ۵]






wiki: قضیه فیثاغورس
