قضیه رأی گیری برترند. فرض کنید در یک انتخابات کاندید A ، a رأی و کاندید B ، b رأی به دست می آورد؛ به طوری که a > k b ( k یک عدد صحیح مثبت است ) . تعداد ( یا احتمال ) حالاتی را به دست آورید که در تمام طول رأی گیری آرای A ، دست کم k تا بیشتر از آرای B باشد. پاسخ a − k b a + b ( a + b a ) است. ( احتمال آن برای حالت k = 1 برابر با a − b a + b است. ) [ ۱]
در سال ۱۸۸۷ جوزف برترند که مسئلهٔ رأی گیری را بیان کرده بود برای حالت خاص k = 1 راه حلی از طریق روابط بازگشتی ارائه داد و خواستار راه حل مستقیمی برای آن شد. بلافاصله بعد از آن که برترند پرسش خود را مطرح کرد E ́mile Barbier راه حلی برای هر k اختیاری مطرح کرد اما هیچ اثباتی برای آن نداشت. اندکی بعد Désiré André اثبات ترکیبیاتی کوتاهی برای حالت k = 1 مسئلهٔ برترند داد. در سال ۱۹۲۳ Aeppli اعلام کرد که اولین اثبات برای قضیهٔ رأی گیری به ازای k ≥ 1 دارد و به خوانندگان مشتاق مقالهٔ دکتری خود را پیشنهاد کرد.
فرض کنید k = 1 است. ۵ رأی دهنده داریم که ۳نفر به A و ۲نفر به B رأی خواهند داد. ( 1 × 2 ≤ 3 ) می خواهیم در طول رأی گیری همواره تعداد رای های A بیشتر از B باشد. ۱۰ حالت برای ترتیب رأی ها وجود دارد:
• A A A B B {\displaystyle AAABB}
• A A B A B {\displaystyle AABAB}
• A B A A B {\displaystyle ABAAB}
• B A A A B {\displaystyle BAAAB}
• A A B B A {\displaystyle AABBA}
• A B A B A {\displaystyle ABABA}
• B A A B A {\displaystyle BAABA}
• A B B A A {\displaystyle ABBAA}
• B A B A A {\displaystyle BABAA}
• B B A A A {\displaystyle BBAAA}
در جدول زیر تعداد آرای هر کاندید را در هر مرحله از رأی گیری برای حالت B A B A A بررسی می کنیم:
برای هر ستون تعداد آرای A بیشتر از B است. برای حالت A A B B A در هر مرحله از رأی گیری داریم:
در این حالت تعداد رأی های B در مرحلهٔ چهارم به A رسیده. از بین ۱۰حالت ممکن برای ترتیب آرا تنها در ۲حالت A A B A B و A A A B B همواره تعداد رای های A بیشتر از B است که برابر مقدار 3 − 2 3 + 2 ( 5 3 ) می باشد. و احتمال آن 2 10 است که برابر 3 − 2 3 + 2 می باشد.
آندره برای به دست آوردن تعداد حالت های مطلوب مسئله، حالت های نامطلوب را از تعداد کل حالات کم کرد. فرض کنید تعداد آرای کاندید A ، a تا و تعداد آرای کاندید B ، b تا باشد. می دانیم تمام جایگشت هایی که با B شروع شوند نامطلوبند. می خواهیم تناظر یک به یکی بین جایگشت های نامطلوبی که با A شروع می شوند و تمام جایگشت هایی که با B شروع می شوند برقرار کنیم. گره را نقطه ای تعریف می کنیم که تعداد رأی های A و B برابر باشند. اگر همواره آرای A بیشتر از B باشد نباید به گره ای برخورد کنیم. از آنجایی که تعداد رأی های A بیشتر از B است اگر رأی اول برای کاندید B باشد بالاخره به گره می رسیم. برای هر رشته که با A شروع شود و گره داشته باشد رأی ها را تا رسیدن به اولین گره معکوس می کنیم ( یعنی هر A را به B تبدیل می کنیم و برعکس ) و رشته ای که با B شروع می شود می سازیم. به طور مشابه هر رشته ای که با B شروع می شود را به رشته ای که با A شروع می شود و گره دارد ( نامطلوب است ) تبدیل می کنیم. ( می دانیم معکوس معکوس هر رأی همان رأی است. اگر ۲تبدیل یافته یکسان باشند معکوس تا گرهٔ اول آن ها که همان رشته هایی هستند که از آنها به دست آمده اند هم یکسان اند پس این تبدیل ها یک به یک است ) در نتیجه تناظری یک به یک داریم. تعداد حالاتی که با B شروع می شوند معادل جایگشت هایی است که می توان با a تا A و b − 1 تا B ساخت یعنی ( a + b − 1 b − 1 ) . در نتیجه تعداد حالات مطلوب از روابط زیر به دست می آید: ( a + b a ) − 2 ( a + b − 1 a ) = a − b a + b ( a + b a ) و احتمال و قوع آن برابر a − b a + b ( a + b a ) ( a + b a ) = a − b a + b خواهدبود. [ ۲]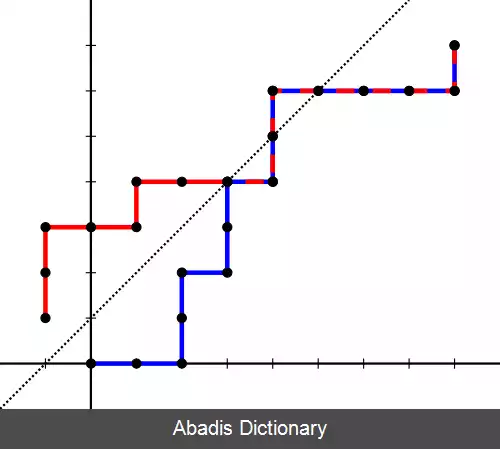
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر سال ۱۸۸۷ جوزف برترند که مسئلهٔ رأی گیری را بیان کرده بود برای حالت خاص k = 1 راه حلی از طریق روابط بازگشتی ارائه داد و خواستار راه حل مستقیمی برای آن شد. بلافاصله بعد از آن که برترند پرسش خود را مطرح کرد E ́mile Barbier راه حلی برای هر k اختیاری مطرح کرد اما هیچ اثباتی برای آن نداشت. اندکی بعد Désiré André اثبات ترکیبیاتی کوتاهی برای حالت k = 1 مسئلهٔ برترند داد. در سال ۱۹۲۳ Aeppli اعلام کرد که اولین اثبات برای قضیهٔ رأی گیری به ازای k ≥ 1 دارد و به خوانندگان مشتاق مقالهٔ دکتری خود را پیشنهاد کرد.
فرض کنید k = 1 است. ۵ رأی دهنده داریم که ۳نفر به A و ۲نفر به B رأی خواهند داد. ( 1 × 2 ≤ 3 ) می خواهیم در طول رأی گیری همواره تعداد رای های A بیشتر از B باشد. ۱۰ حالت برای ترتیب رأی ها وجود دارد:
• A A A B B {\displaystyle AAABB}
• A A B A B {\displaystyle AABAB}
• A B A A B {\displaystyle ABAAB}
• B A A A B {\displaystyle BAAAB}
• A A B B A {\displaystyle AABBA}
• A B A B A {\displaystyle ABABA}
• B A A B A {\displaystyle BAABA}
• A B B A A {\displaystyle ABBAA}
• B A B A A {\displaystyle BABAA}
• B B A A A {\displaystyle BBAAA}
در جدول زیر تعداد آرای هر کاندید را در هر مرحله از رأی گیری برای حالت B A B A A بررسی می کنیم:
برای هر ستون تعداد آرای A بیشتر از B است. برای حالت A A B B A در هر مرحله از رأی گیری داریم:
در این حالت تعداد رأی های B در مرحلهٔ چهارم به A رسیده. از بین ۱۰حالت ممکن برای ترتیب آرا تنها در ۲حالت A A B A B و A A A B B همواره تعداد رای های A بیشتر از B است که برابر مقدار 3 − 2 3 + 2 ( 5 3 ) می باشد. و احتمال آن 2 10 است که برابر 3 − 2 3 + 2 می باشد.
آندره برای به دست آوردن تعداد حالت های مطلوب مسئله، حالت های نامطلوب را از تعداد کل حالات کم کرد. فرض کنید تعداد آرای کاندید A ، a تا و تعداد آرای کاندید B ، b تا باشد. می دانیم تمام جایگشت هایی که با B شروع شوند نامطلوبند. می خواهیم تناظر یک به یکی بین جایگشت های نامطلوبی که با A شروع می شوند و تمام جایگشت هایی که با B شروع می شوند برقرار کنیم. گره را نقطه ای تعریف می کنیم که تعداد رأی های A و B برابر باشند. اگر همواره آرای A بیشتر از B باشد نباید به گره ای برخورد کنیم. از آنجایی که تعداد رأی های A بیشتر از B است اگر رأی اول برای کاندید B باشد بالاخره به گره می رسیم. برای هر رشته که با A شروع شود و گره داشته باشد رأی ها را تا رسیدن به اولین گره معکوس می کنیم ( یعنی هر A را به B تبدیل می کنیم و برعکس ) و رشته ای که با B شروع می شود می سازیم. به طور مشابه هر رشته ای که با B شروع می شود را به رشته ای که با A شروع می شود و گره دارد ( نامطلوب است ) تبدیل می کنیم. ( می دانیم معکوس معکوس هر رأی همان رأی است. اگر ۲تبدیل یافته یکسان باشند معکوس تا گرهٔ اول آن ها که همان رشته هایی هستند که از آنها به دست آمده اند هم یکسان اند پس این تبدیل ها یک به یک است ) در نتیجه تناظری یک به یک داریم. تعداد حالاتی که با B شروع می شوند معادل جایگشت هایی است که می توان با a تا A و b − 1 تا B ساخت یعنی ( a + b − 1 b − 1 ) . در نتیجه تعداد حالات مطلوب از روابط زیر به دست می آید: ( a + b a ) − 2 ( a + b − 1 a ) = a − b a + b ( a + b a ) و احتمال و قوع آن برابر a − b a + b ( a + b a ) ( a + b a ) = a − b a + b خواهدبود. [ ۲]

wiki: قضیه رأی گیری برترند
