قضیه تالس یکی از قضایای مهم در هندسه مقدماتی است که می گوید: اگر دو خط راستِ موازی با یکدیگر ، دو خط متقاطع را قطع کنند، آنگاه بر روی آن دو خط متقاطع پاره خط های متناسب ایجاد می شود.
قضیه تالس نیز مانند سایر قضایا هندسی دو شرطی است ( عکس آن برقرار است ) بنابراین درعکس قضیه تالس یا شرط دوم آن اگر خطی از دو ضلع مثلث ، پاره خط های متناسب ایجاد کند آن خط موازی ضلع سوم است. ( BC موازی با DE )
هزار و سیصد سال قبل از تولد تالس مصریان باستان قضیهٔ تالس را می دانستند؛ درواقع در راه حل مسئلهٔ شماره ۵۳ پاپیروس رایند از معادل قضیهٔ تالس استفاده می شود. [ ۱]
با توجه به منابع تاریخی یونان باستان، تالس ریاضی دان یونانی با استفاده از این قضیه توانست ارتفاع هرم خئوپس را به دست آورد. [ ۲]
قضیهٔ دوم مقالهٔ ششم اصول اقلیدس به اثبات قضیهٔ تالس و عکس آن می پردازد.
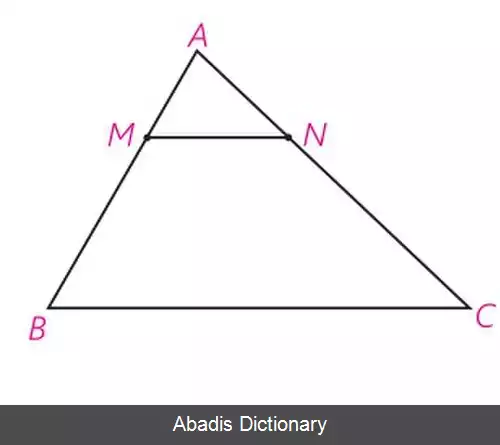
اگر خط راستی موازی با یکی از اضلاع مثلث رسم شود، دو ضلع دیگر را به یک نسبت می برد. ( قضیه ۲ مقالهٔ ششم )
"فرض می کنیم DE موازی با BC یکی از اضلاع مثلث ABC رسم شده است. می خواهیم اثبات کنیم نسبت BD به AD مثل نسبت CE است به AE.
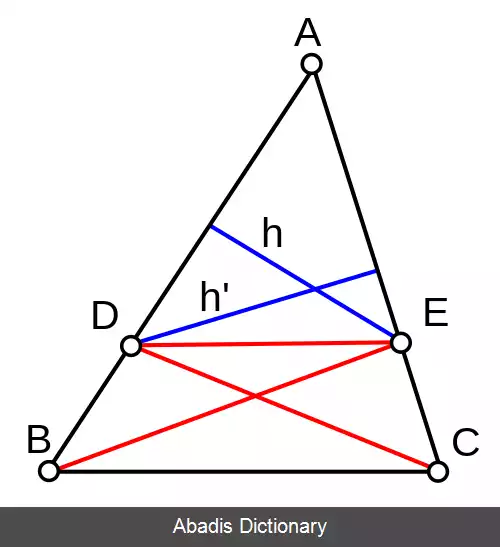
E را به B و D را به C وصل می کنیم؛ بنابراین مساحت مثلث BDE با مساحت مثلث CDE مساوی است. زیرا هر دو دارای یک قاعدهٔ DE هستند و رأسهای آنها بر خط راست BC، موازی با قاعدهٔ DE قرار دارد؛"
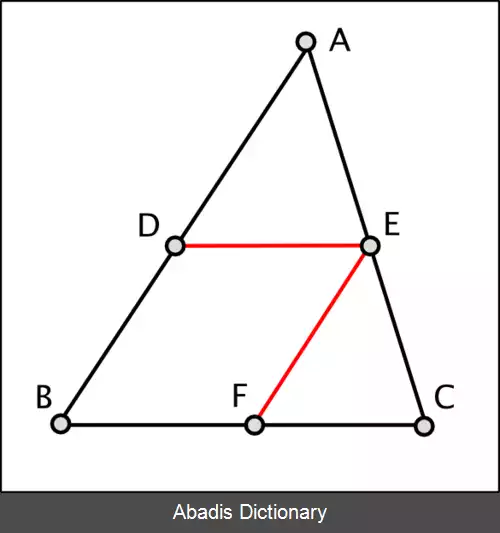
D E ∥ B C ⟹ | △ B D E | = | △ C D E | "از آن جایی که نسبت های کمیت های متساوی به یک کمیت با هم مساوی اند پس نسبت مساحت مثلث BDE به مثلث ADE مثل نسبت مساحت مثلث CDE است به مثلث ADE. از طرفی نسبت مساحت مثلث BDE به مساحت مثلث ADE، مثل نسبت BD است به DA؛ زیرا دارای یک ارتفاع اند که از E بر AB عمود می شود و نسبت آنها به یکدیگر مثل نسبت قاعده های آنهاست. به طور مشابه نسبت مساحت مثلث CDE به مساحت مثلث ADE مثل نسبت CE است به EA. بنابراین نسبت BD به DA نیز مثل نسبت CE است به EA. "[ ۳] | △ B D E | | △ A D E | = | △ C D E | | △ A D E | = C E . h ′ E A . h ′ = B D . h A D . h ⇒ C E E A = B D A D تعمیم های قضیه تالس اگر خطی دو ضلع مثلثی را در دو نقطه قطع کند و با ضلع سوم آن موازی باشد، مثلثی پدید می آید که اندازهٔ ضلع های آن با اندازهٔ مثلث اصلی متناسب است.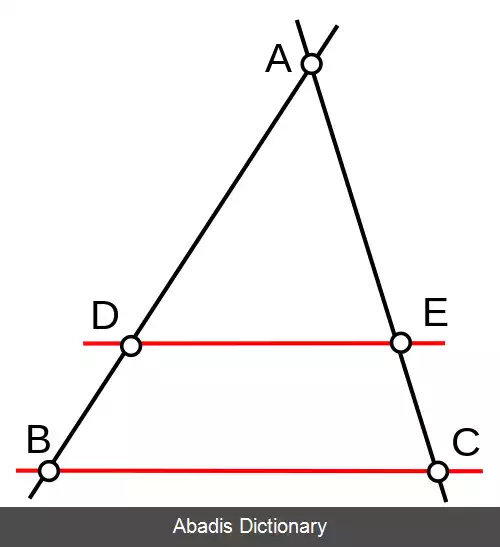

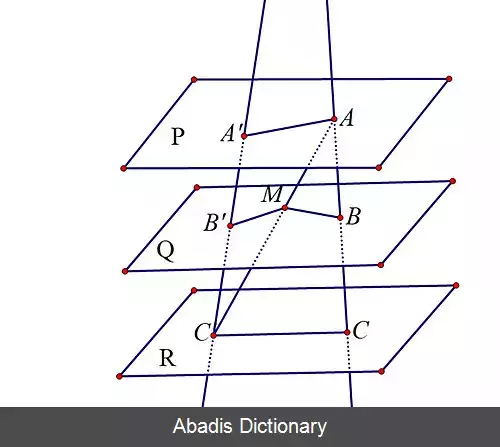
قضیه تالس نیز مانند سایر قضایا هندسی دو شرطی است ( عکس آن برقرار است ) بنابراین درعکس قضیه تالس یا شرط دوم آن اگر خطی از دو ضلع مثلث ، پاره خط های متناسب ایجاد کند آن خط موازی ضلع سوم است. ( BC موازی با DE )
هزار و سیصد سال قبل از تولد تالس مصریان باستان قضیهٔ تالس را می دانستند؛ درواقع در راه حل مسئلهٔ شماره ۵۳ پاپیروس رایند از معادل قضیهٔ تالس استفاده می شود. [ ۱]
با توجه به منابع تاریخی یونان باستان، تالس ریاضی دان یونانی با استفاده از این قضیه توانست ارتفاع هرم خئوپس را به دست آورد. [ ۲]
قضیهٔ دوم مقالهٔ ششم اصول اقلیدس به اثبات قضیهٔ تالس و عکس آن می پردازد.
اگر خط راستی موازی با یکی از اضلاع مثلث رسم شود، دو ضلع دیگر را به یک نسبت می برد. ( قضیه ۲ مقالهٔ ششم )
"فرض می کنیم DE موازی با BC یکی از اضلاع مثلث ABC رسم شده است. می خواهیم اثبات کنیم نسبت BD به AD مثل نسبت CE است به AE.
E را به B و D را به C وصل می کنیم؛ بنابراین مساحت مثلث BDE با مساحت مثلث CDE مساوی است. زیرا هر دو دارای یک قاعدهٔ DE هستند و رأسهای آنها بر خط راست BC، موازی با قاعدهٔ DE قرار دارد؛"
D E ∥ B C ⟹ | △ B D E | = | △ C D E | "از آن جایی که نسبت های کمیت های متساوی به یک کمیت با هم مساوی اند پس نسبت مساحت مثلث BDE به مثلث ADE مثل نسبت مساحت مثلث CDE است به مثلث ADE. از طرفی نسبت مساحت مثلث BDE به مساحت مثلث ADE، مثل نسبت BD است به DA؛ زیرا دارای یک ارتفاع اند که از E بر AB عمود می شود و نسبت آنها به یکدیگر مثل نسبت قاعده های آنهاست. به طور مشابه نسبت مساحت مثلث CDE به مساحت مثلث ADE مثل نسبت CE است به EA. بنابراین نسبت BD به DA نیز مثل نسبت CE است به EA. "[ ۳] | △ B D E | | △ A D E | = | △ C D E | | △ A D E | = C E . h ′ E A . h ′ = B D . h A D . h ⇒ C E E A = B D A D تعمیم های قضیه تالس اگر خطی دو ضلع مثلثی را در دو نقطه قطع کند و با ضلع سوم آن موازی باشد، مثلثی پدید می آید که اندازهٔ ضلع های آن با اندازهٔ مثلث اصلی متناسب است.






wiki: قضیه تالس
قضیه تالس (دایره). قضیه تالس در هندسه این مطلب را بیان می کند که اگر A و B و C نقاط روی دایره باشند و خط AC قطر دایره باشد، آن وقت زاویه ABC یک زاویهٔ قائمه خواهد بود. به بیان دیگر مرکز دایره محیطی مثلث روی یکی از اضلاع مثلث قرار می گیرد، اگر و تنها اگر آن مثلث قائم الزاویه باشد.
تالس اولین کسی نبود که این قضیه را کشف کرد؛ قبل از او مصریان و بابلیان این قضیه را می دانستند ولی تالس آن را اثبات کرد و به نام او نیز معروف شد.
فرض کنیم O مرکز دایره باشد. آنگاه O A = O B = O C و △ O A B و △ O B C متساوی الساقین خواهند بود. در نتیجه B A O ^ = A B O ^ و O C B ^ = O B C ^ .
فرض کنیم α = A B O ^ و β = O C B ^ . چون جمع زوایای داخلی مثلث برابر ۱۸۰ درجه است پس:
O C B ^ + A B C ^ + B A O ^ = 2 α + 2 β = 180 ∘ ⇒ α + β = 90 ∘
A B C ^ = α + β = 90 ∘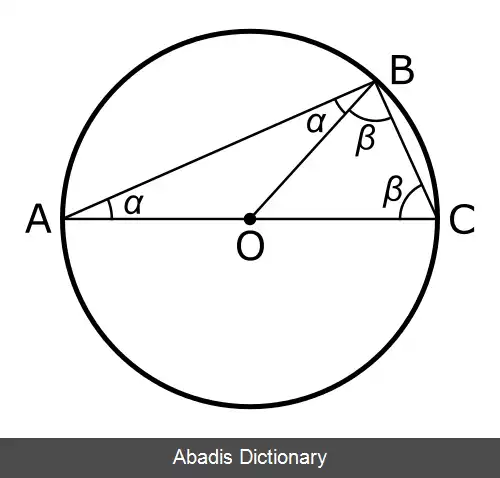

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتالس اولین کسی نبود که این قضیه را کشف کرد؛ قبل از او مصریان و بابلیان این قضیه را می دانستند ولی تالس آن را اثبات کرد و به نام او نیز معروف شد.
فرض کنیم O مرکز دایره باشد. آنگاه O A = O B = O C و △ O A B و △ O B C متساوی الساقین خواهند بود. در نتیجه B A O ^ = A B O ^ و O C B ^ = O B C ^ .
فرض کنیم α = A B O ^ و β = O C B ^ . چون جمع زوایای داخلی مثلث برابر ۱۸۰ درجه است پس:
O C B ^ + A B C ^ + B A O ^ = 2 α + 2 β = 180 ∘ ⇒ α + β = 90 ∘
A B C ^ = α + β = 90 ∘



wiki: قضیه تالس (دایره)
