قانون آمپر. در الکترومغناطیس، قانون آمپر، میدان مغناطیسی روی یک مسیر بسته فرضی به دور یک سیم را به جریان الکتریکی سیم ربط می دهد. قانون آمپر یکی از معادلات ماکسول است و نخستین بار آندره - ماری آمپر آن را پیش نهاد.
قانون آمپر در شکل اولیهٔ خود میدان مغناطیسی را تنها به جریان الکتریکی ربط می دهد. این قانون در حالت کلی درست نیست ( بخش بعدی را ببینید ) ، ولی در شرایط خاصی که میدان الکتریکی نسبت به زمان تغییر نکند، درست است. قانون آمپر را بنا به مورد استفاده به دو صورت انتگرالی و دیفرانسیلی می توان نوشت.
صورت انتگرالی قانون آمپر در اس آی به صورت زیر است:
که در آن:
• ∮ C {\displaystyle \oint _{C}} انتگرال خطی بسته حول مسیر C،
• B {\displaystyle \mathbf {B} } میدان مغناطیسی برحسب تسلا،
• ⋅ {\displaystyle \cdot } ضرب داخلی برداری،
• d l {\displaystyle \mathrm {d} \mathbf {l} } المان خط روی مسیر C،
• ∬ S {\displaystyle \iint _{S}} انتگرال دوگانه روی سطح S محصور شده توسط منحنی C،
• μ 0 {\displaystyle \mu _{0}\!\ } ثابت تراوایی خلاء،
• J {\displaystyle \mathbf {J} } چگالی جریان الکتریکی است که از داخل مسیر C و از سطح S می گذرد.
• d S {\displaystyle \mathrm {d} \mathbf {S} \!\ } المان سطح برداری S است.
• I e n c {\displaystyle I_{\mathrm {enc} }\!\ } جریان متوسط عبوری از سطح S است.
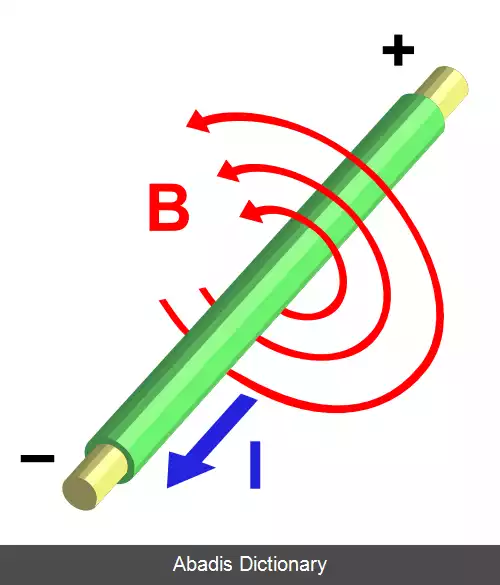
جهت جریان الکتریکی و میدان مغناطیسی را می توان با استفاده از قانون دست راست به دست آورد.
صورت دیفرانسیلی قانون آمپر در دستگاه SI چنین است:
• ∇ × {\displaystyle \mathbf {\nabla } \times } عملگر کرل،
• B {\displaystyle \mathbf {B} } میدان مغناطیسی برحسب تسلا،
• J {\displaystyle \mathbf {J} } چگالی جریان الکتریکی،
• μ 0 {\displaystyle \mu _{0}\!\ } ثابت تراوایی خلاء است.
در ۱۸۶۱ جیمز کلارک ماکسول جریان جابجایی را نیز به قانون اولیه آمپر افزود و آن را به صورت تعمیم یافته زیر نوشت:[ ۱]
که در آن ϵ 0 ثابت گذردهی خلاء و E میدان الکتریکی است. این معادله تعمیم یافته صورت دیفرانسیلی به صورت زیر دارد: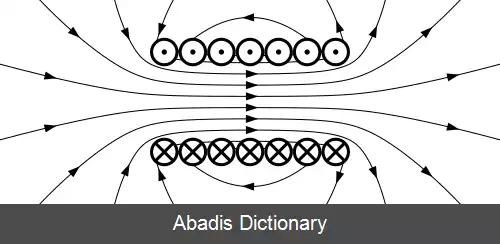
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفقانون آمپر در شکل اولیهٔ خود میدان مغناطیسی را تنها به جریان الکتریکی ربط می دهد. این قانون در حالت کلی درست نیست ( بخش بعدی را ببینید ) ، ولی در شرایط خاصی که میدان الکتریکی نسبت به زمان تغییر نکند، درست است. قانون آمپر را بنا به مورد استفاده به دو صورت انتگرالی و دیفرانسیلی می توان نوشت.
صورت انتگرالی قانون آمپر در اس آی به صورت زیر است:
که در آن:
• ∮ C {\displaystyle \oint _{C}} انتگرال خطی بسته حول مسیر C،
• B {\displaystyle \mathbf {B} } میدان مغناطیسی برحسب تسلا،
• ⋅ {\displaystyle \cdot } ضرب داخلی برداری،
• d l {\displaystyle \mathrm {d} \mathbf {l} } المان خط روی مسیر C،
• ∬ S {\displaystyle \iint _{S}} انتگرال دوگانه روی سطح S محصور شده توسط منحنی C،
• μ 0 {\displaystyle \mu _{0}\!\ } ثابت تراوایی خلاء،
• J {\displaystyle \mathbf {J} } چگالی جریان الکتریکی است که از داخل مسیر C و از سطح S می گذرد.
• d S {\displaystyle \mathrm {d} \mathbf {S} \!\ } المان سطح برداری S است.
• I e n c {\displaystyle I_{\mathrm {enc} }\!\ } جریان متوسط عبوری از سطح S است.
جهت جریان الکتریکی و میدان مغناطیسی را می توان با استفاده از قانون دست راست به دست آورد.
صورت دیفرانسیلی قانون آمپر در دستگاه SI چنین است:
• ∇ × {\displaystyle \mathbf {\nabla } \times } عملگر کرل،
• B {\displaystyle \mathbf {B} } میدان مغناطیسی برحسب تسلا،
• J {\displaystyle \mathbf {J} } چگالی جریان الکتریکی،
• μ 0 {\displaystyle \mu _{0}\!\ } ثابت تراوایی خلاء است.
در ۱۸۶۱ جیمز کلارک ماکسول جریان جابجایی را نیز به قانون اولیه آمپر افزود و آن را به صورت تعمیم یافته زیر نوشت:[ ۱]
که در آن ϵ 0 ثابت گذردهی خلاء و E میدان الکتریکی است. این معادله تعمیم یافته صورت دیفرانسیلی به صورت زیر دارد:


wiki: قانون آمپر
