فرایند وینر، یک فرایند تصادفی پیوسته در زمان در ریاضیات است که به افتخار نوربرت وینر نامگذاری شده است. این فرایند به اسم حرکت براونی استاندارد هم شناخته می شود، به خاطر کارهای رابرت براون. این یکی از بهترین فرایند هایLévy است. ( فرایند تصادفی Càdlàg با خاصیت رشد مستقل مانا ) و در ریاضیات محض و کاربردی، اقتصاد، مالیه ریاضی و فیزیک کاربردهای زیادی دارد.
فرایند وینر هم در ریاضیات محض و هم در ریاضبات کاربردی کاربرد دارد. کاربرد آن در ریاضیات محض برای بررسی زمان - پیوسته مدل مارتینگل ( martingales ) است که یک مدل برای بررسی این است که چقدر یک فرایند تصادفی می تواند پیچیده باشد است. در نتیجه نقش حیاتی درمحاسبات احتمالی و انتشار فرایندها و حتی نظریه پتانسیل دارد. این فرایند از Schramm–Loewner تکامل نتیجه می شود. در ریاضیات کاربردی، فرایند وینر برای نشان دادن تجمیع نویز سفید فرایند گوسی استفاده می شود بنابراین در مهندسی الکترونیک برای مدل کردن نویز از آن استفاده می شود ( نویز Brownian را هم ببینید. ) همچنین به عنوان ابزار خطا در تئوری فیلتر و نیروهای ناشناخته در تئوری کنترل کاربرد دارد.
فرایند وینردر سراسر علوم محاسباتی کاربردهای متنوعی دارد. در فیزیک از آن برای مطالعه حرکت براونی استفاده می شود همچنین در مطالعه دربارهٔ انتشار ذرات معلق در مایع و انواع دیگر انتشار به صورت فوکر–پلانک و معادلات انگوین کاربرد دارد. همچنین پایه های دقیقی برای توصیف فرمولبندی مسیر انتگرال در مکانیک کوانتومی به ما می دهد ( با فرایند وینر و به وسیله فرمول فاینمن - کاک می توان یک راه حل برای معادله شرودینگر ارائه داد. ) و برای مطالعه تورم ابدی در کیهان شناسی فیزیکی نیز کاربرد دارد. این فرایند نقش برجسته ای در تئوری ریاضی امور مالی به ویژه Black–Scholes به عنوان مدلی برای قیمت گذاری دارد.
فرایند وینر Wt با مشخصه زیر تعیین می شود:[ ۱]
• به صورت قریب به یقین W0 = ۰
• W رشد مستقل داشته باشد: یعنی Wt+u - Wt مستقل از ( σ ( Ws: s ≤ t برای u ≥ ۰
• W رشد گوسی داشته باشد: یعنی Wt+u - Wt توزیع نرمال با میانگین ۰ و واریانس u باشد. Wt+u−Wt
N ( 0, u )
• W مسیر پبوسته باشد: یعنی با احتمال ۱تابع Wt در t پیوسته باشد.
رشد مستقل داشته باشد به این معنی است که اگر ۰ ≤ s1 < t1 ≤ s2 < t2 آنگاه Wt1−Ws1 و Wt2−Ws2 متغیر تصادفی مستقل باشند.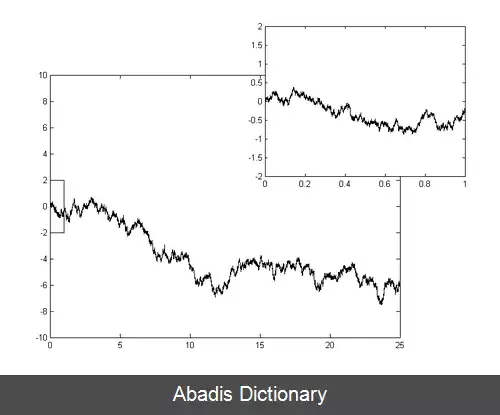
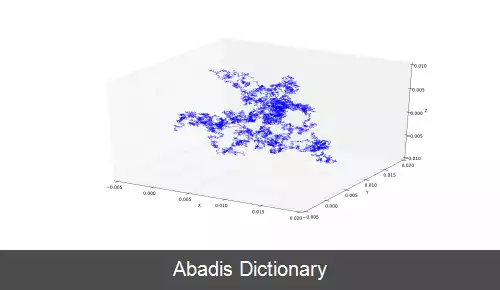

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرایند وینر هم در ریاضیات محض و هم در ریاضبات کاربردی کاربرد دارد. کاربرد آن در ریاضیات محض برای بررسی زمان - پیوسته مدل مارتینگل ( martingales ) است که یک مدل برای بررسی این است که چقدر یک فرایند تصادفی می تواند پیچیده باشد است. در نتیجه نقش حیاتی درمحاسبات احتمالی و انتشار فرایندها و حتی نظریه پتانسیل دارد. این فرایند از Schramm–Loewner تکامل نتیجه می شود. در ریاضیات کاربردی، فرایند وینر برای نشان دادن تجمیع نویز سفید فرایند گوسی استفاده می شود بنابراین در مهندسی الکترونیک برای مدل کردن نویز از آن استفاده می شود ( نویز Brownian را هم ببینید. ) همچنین به عنوان ابزار خطا در تئوری فیلتر و نیروهای ناشناخته در تئوری کنترل کاربرد دارد.
فرایند وینردر سراسر علوم محاسباتی کاربردهای متنوعی دارد. در فیزیک از آن برای مطالعه حرکت براونی استفاده می شود همچنین در مطالعه دربارهٔ انتشار ذرات معلق در مایع و انواع دیگر انتشار به صورت فوکر–پلانک و معادلات انگوین کاربرد دارد. همچنین پایه های دقیقی برای توصیف فرمولبندی مسیر انتگرال در مکانیک کوانتومی به ما می دهد ( با فرایند وینر و به وسیله فرمول فاینمن - کاک می توان یک راه حل برای معادله شرودینگر ارائه داد. ) و برای مطالعه تورم ابدی در کیهان شناسی فیزیکی نیز کاربرد دارد. این فرایند نقش برجسته ای در تئوری ریاضی امور مالی به ویژه Black–Scholes به عنوان مدلی برای قیمت گذاری دارد.
فرایند وینر Wt با مشخصه زیر تعیین می شود:[ ۱]
• به صورت قریب به یقین W0 = ۰
• W رشد مستقل داشته باشد: یعنی Wt+u - Wt مستقل از ( σ ( Ws: s ≤ t برای u ≥ ۰
• W رشد گوسی داشته باشد: یعنی Wt+u - Wt توزیع نرمال با میانگین ۰ و واریانس u باشد. Wt+u−Wt
N ( 0, u )
• W مسیر پبوسته باشد: یعنی با احتمال ۱تابع Wt در t پیوسته باشد.
رشد مستقل داشته باشد به این معنی است که اگر ۰ ≤ s1 < t1 ≤ s2 < t2 آنگاه Wt1−Ws1 و Wt2−Ws2 متغیر تصادفی مستقل باشند.



wiki: فرایند وینر
