فاکتوریلِ ( به انگلیسی: Factorial ) هر عدد طبیعی در ریاضیات از حاصل ضرب آن عدد در تمام اعداد طبیعی کوچک تر از آن بدون صفر به دست می آید. فاکتوریل عددی مانند n را n ! می نویسند و «اِن فاکتوریل» می خوانند. همچنین طبق قرارداد، فاکتوریل صفر برابر با یک است. [ ۱]
فاکتوریل برای اولین بار توسط کریستیان کرامپ و در سال ۱۸۰۸ معرفی شد. [ ۲]
تابع فاکتوریل به صورت زیر تعریف شده:
n ! = ∏ k = 1 n k ∀ n ∈ N .
= 1 × 2 × 3 × . . . × ( n − 2 ) × ( n − 1 ) × ( n )
= n × ( n − 1 ) × ( n − 2 ) × . . . × ( 2 ) × ( 1 )
این تابع به شکل توابع بازگشتی به صورت زیر تعریف می شود:
مثال
5 ! = 1 × 2 × 3 × 4 × 5 = 120 6 ! = 1 × 2 × 3 × 4 × 5 × 6 = 720
هر چند توضیحات فوق در رابطه با فاکتوریل کاملاً صحیح است اما نمی تواند توضیح دهد که چرا فاکتوریل صفر برابر با یک است؛ یا اینکه آیا اعداد اعشاری یا منفی هم فاکتوریل دارند یا خیر؟ در واقع فاکتوریل تعریف جامع تری دارد.
فاکتوریل ۰ برابر با ۱ می باشد.
0 ! = 1
بر اساس این تعریف خواهیم داشت:
1 ! = 1 × 0 ! = 1 × 1 = 1
برای محاسبه فاکتوریل بر روی اعداد غیرطبیعی از معادل ریاضیاتی فاکتوریل استفاده می کنیم؛ بنابراین بر اساس تعریف تابع گاما می توانیم به صورت n ! = Γ ( n + 1 ) بنویسیم. در بخش بعد در ارتباط با این تابع بحث شده است.
در سطحی بالاتر تعریفی که برای فاکتوریل ارائه شده و می توان با استفاده از آن فاکتوریل را برای تمام اعداد به جز اعداد صحیح منفی محاسبه کرد. با استفاده از تعریف تابع گاما خواهیم داشت:
n ! = ∫ 0 ∞ t n e − t d t [ ۳]
نکته دیگر در مورد اعداد صحیح منفی این است که مقدار فاکتوریل برای آن ها به سمت بی نهایت میل می کند. فاکتوریل کاربردهای بسیاری در علوم مختلف از جمله فیزیک دارد.
جالب است بدانید که : ( − 1 2 ) ! = π
فاکتوریل زیر پیوند کلیات توابع بشمار می آید که برحسب جز؛ چیدمان از نواحی زیرین توابع موضوع می گیرد
• : log n ! = ∑ x = 1 n log x . {\displaystyle \log n!=\sum _{x=1}^{n}\log x. }
• : e ( n e ) n ≤ n ! ≤ e ( n + 1 e ) n + 1 . {\displaystyle e\left ( {\frac {n}{e}}\right ) ^{n}\leq n!\leq e\left ( {\frac {n+1}{e}}\right ) ^{n+1}. }
• : n ! ≈ 2 π n ( n e ) n . {\displaystyle n!\approx {\sqrt {2\pi n}}\left ( {\frac {n}{e}}\right ) ^{n}. }
• : n ! = Γ ( n + 1 ) . {\displaystyle n!=\Gamma ( n+1 ) . \, }
• : n ! = Π ( n ) = ∏ k = 1 ∞ ( k + 1 k ) n k n + k = ⋯ . {\displaystyle {\begin{aligned}n!=\Pi ( n ) & =\prod _{k=1}^{\infty }\left ( {\frac {k+1}{k}}\right ) ^{n}\!\!{\frac {k}{n+k}}=\left\left\left\cdots . \end{aligned}}}
• : z ! = ∑ n = 0 ∞ g n z n . {\displaystyle z!=\sum _{n=0}^{\infty }g_{n}z^{n}. }
• : ( 2 k − 1 ) ! ! = ∏ i = 1 k ( 2 i − 1 ) = ( 2 k ) ! 2 k k ! = 2 k P k 2 k = ( 2 k ) k _ 2 k . {\displaystyle ( 2k - 1 ) !!=\prod _{i=1}^{k} ( 2i - 1 ) ={\frac { ( 2k ) !}{2^{k}k!}}={\frac {_{2k}P_{k}}{2^{k}}}={\frac {{ ( 2k ) }^{\underline {k}}}{2^{k}}}. }
• : n $ ≡ n ! n ! ⋅ ⋅ ⋅ n ! ⏟ n ! , {\displaystyle n\$\equiv {\begin{matrix}\underbrace {n!^{{n!}^{{\cdot }^{{\cdot }^{{\cdot }^{n!}}}}}} \\n!\end{matrix}}, \, }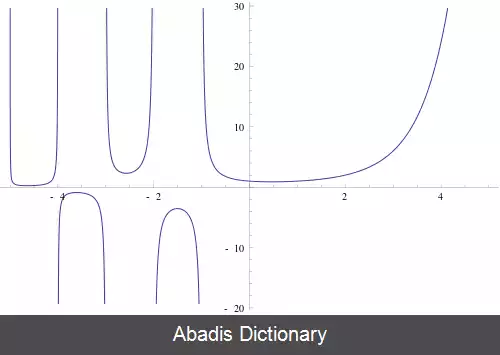
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففاکتوریل برای اولین بار توسط کریستیان کرامپ و در سال ۱۸۰۸ معرفی شد. [ ۲]
تابع فاکتوریل به صورت زیر تعریف شده:
n ! = ∏ k = 1 n k ∀ n ∈ N .
= 1 × 2 × 3 × . . . × ( n − 2 ) × ( n − 1 ) × ( n )
= n × ( n − 1 ) × ( n − 2 ) × . . . × ( 2 ) × ( 1 )
این تابع به شکل توابع بازگشتی به صورت زیر تعریف می شود:
مثال
5 ! = 1 × 2 × 3 × 4 × 5 = 120 6 ! = 1 × 2 × 3 × 4 × 5 × 6 = 720
هر چند توضیحات فوق در رابطه با فاکتوریل کاملاً صحیح است اما نمی تواند توضیح دهد که چرا فاکتوریل صفر برابر با یک است؛ یا اینکه آیا اعداد اعشاری یا منفی هم فاکتوریل دارند یا خیر؟ در واقع فاکتوریل تعریف جامع تری دارد.
فاکتوریل ۰ برابر با ۱ می باشد.
0 ! = 1
بر اساس این تعریف خواهیم داشت:
1 ! = 1 × 0 ! = 1 × 1 = 1
برای محاسبه فاکتوریل بر روی اعداد غیرطبیعی از معادل ریاضیاتی فاکتوریل استفاده می کنیم؛ بنابراین بر اساس تعریف تابع گاما می توانیم به صورت n ! = Γ ( n + 1 ) بنویسیم. در بخش بعد در ارتباط با این تابع بحث شده است.
در سطحی بالاتر تعریفی که برای فاکتوریل ارائه شده و می توان با استفاده از آن فاکتوریل را برای تمام اعداد به جز اعداد صحیح منفی محاسبه کرد. با استفاده از تعریف تابع گاما خواهیم داشت:
n ! = ∫ 0 ∞ t n e − t d t [ ۳]
نکته دیگر در مورد اعداد صحیح منفی این است که مقدار فاکتوریل برای آن ها به سمت بی نهایت میل می کند. فاکتوریل کاربردهای بسیاری در علوم مختلف از جمله فیزیک دارد.
جالب است بدانید که : ( − 1 2 ) ! = π
فاکتوریل زیر پیوند کلیات توابع بشمار می آید که برحسب جز؛ چیدمان از نواحی زیرین توابع موضوع می گیرد
• : log n ! = ∑ x = 1 n log x . {\displaystyle \log n!=\sum _{x=1}^{n}\log x. }
• : e ( n e ) n ≤ n ! ≤ e ( n + 1 e ) n + 1 . {\displaystyle e\left ( {\frac {n}{e}}\right ) ^{n}\leq n!\leq e\left ( {\frac {n+1}{e}}\right ) ^{n+1}. }
• : n ! ≈ 2 π n ( n e ) n . {\displaystyle n!\approx {\sqrt {2\pi n}}\left ( {\frac {n}{e}}\right ) ^{n}. }
• : n ! = Γ ( n + 1 ) . {\displaystyle n!=\Gamma ( n+1 ) . \, }
• : n ! = Π ( n ) = ∏ k = 1 ∞ ( k + 1 k ) n k n + k = ⋯ . {\displaystyle {\begin{aligned}n!=\Pi ( n ) & =\prod _{k=1}^{\infty }\left ( {\frac {k+1}{k}}\right ) ^{n}\!\!{\frac {k}{n+k}}=\left\left\left\cdots . \end{aligned}}}
• : z ! = ∑ n = 0 ∞ g n z n . {\displaystyle z!=\sum _{n=0}^{\infty }g_{n}z^{n}. }
• : ( 2 k − 1 ) ! ! = ∏ i = 1 k ( 2 i − 1 ) = ( 2 k ) ! 2 k k ! = 2 k P k 2 k = ( 2 k ) k _ 2 k . {\displaystyle ( 2k - 1 ) !!=\prod _{i=1}^{k} ( 2i - 1 ) ={\frac { ( 2k ) !}{2^{k}k!}}={\frac {_{2k}P_{k}}{2^{k}}}={\frac {{ ( 2k ) }^{\underline {k}}}{2^{k}}}. }
• : n $ ≡ n ! n ! ⋅ ⋅ ⋅ n ! ⏟ n ! , {\displaystyle n\$\equiv {\begin{matrix}\underbrace {n!^{{n!}^{{\cdot }^{{\cdot }^{{\cdot }^{n!}}}}}} \\n!\end{matrix}}, \, }

wiki: فاکتوریل
