در ریاضیات، ضرب نرده ای ( به انگلیسی: scalar multiplication ) یکی از عملگرهای اصلی برای تعریف یک فضای برداری در جبر خطی است ( یا به طور کلی، یک مدول در جبر مجرد ) . [ ۱] [ ۲]
در هندسه، ضرب نرده ای به معنی ضرب یک کمیت نرده ای حقیقی در یک بردار اقلیدسی است. ضرب یک مقدار مثبت، طول بردار را تغییر می دهد، بی آن که جهتش را تغییر دهد؛ در حالی که ضرب یک عدد منفی، جهت بردار را نیز تغییر می دهد. در ضرب نرده ای، راستای بردار ثابت می ماند.
اگر F یک میدان مثل R و V یک فضای برداری روی F باشد، ضرب نرده ای با نماد ⋅ ، تابعی از F × V به V است. نتیجهٔ این تابع ( ضرب مقدار k ∈ F در بردار v ∈ V ) را با k ⋅ v یا k v نشان می دهیم.
⋅ : F × V → V
طبق تعریف یک عملگر، V باید نسبت به ضرب نرده ای بسته باشد.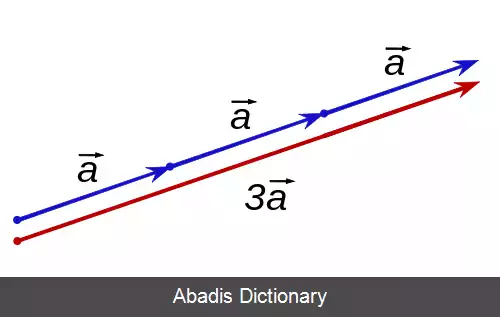
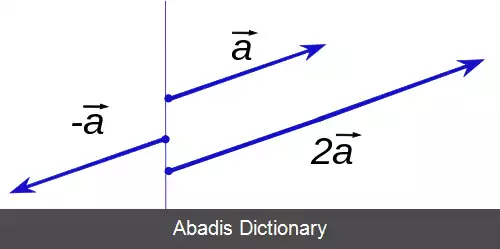
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر هندسه، ضرب نرده ای به معنی ضرب یک کمیت نرده ای حقیقی در یک بردار اقلیدسی است. ضرب یک مقدار مثبت، طول بردار را تغییر می دهد، بی آن که جهتش را تغییر دهد؛ در حالی که ضرب یک عدد منفی، جهت بردار را نیز تغییر می دهد. در ضرب نرده ای، راستای بردار ثابت می ماند.
اگر F یک میدان مثل R و V یک فضای برداری روی F باشد، ضرب نرده ای با نماد ⋅ ، تابعی از F × V به V است. نتیجهٔ این تابع ( ضرب مقدار k ∈ F در بردار v ∈ V ) را با k ⋅ v یا k v نشان می دهیم.
⋅ : F × V → V
طبق تعریف یک عملگر، V باید نسبت به ضرب نرده ای بسته باشد.


wiki: ضرب نرده ای
