صفحات کریستالی اندیس میلر:
ساختار کریستالی اتمی کریستال ها اغلب ناهمسان گر از لحاظ جهات کریستالی است که این غیر یکنواختی بر روی بعضی از خواص کریستال از جمله تغیر شکل پلاستیک تأثیر بسزایی دارد همچنین بعضی از خواص فیزیکی، تابع فاصله ی بین دو اتم مجاور در یک شبکه کریستالی و تعداد پیوند های بین آن ها است. بدین جهت برای تعیین موقعیت صفحات و جهات مختلف در هر شبکه کریستالی می توان از یک روش استاندارد شده استفاده کرد و این عمل به کمک اندیس میلر به صورت زیر انجام می گیرد. ابتدا یک سیستم محور مختصات فضایی که مبدا مختصات آن بر یکی از گوشه های سلول واحد منطبق و محور های آن در جهات مناسبی نسبت به محور های سلول واحد باشد انتخاب می کنیم ( جهات مناسب :جهاتی است که معمولاً موازی با محور های کریستال باشند ) به عنوان مثال در سیستم کریستالی مکعب و تتراگونال از یک سیستم محور مختصات عمود بر هم که مبدا مختصات آن منطبق یکی از گوشه های آن ومحور های مختصات
( x, y, z ) در امتداد سه ضلع عمود بر هم در آن گوشه سلول واحد باشد استفاده می کنیم به عنوان واحد اندازه گیری بر روی محور هاطول اضلاع سلول واحد کریستال یعنی ( a, b, C ) را انتخاب میکنیم در سیستم مکعب طول بردار ها برابر است و برابر واحد انتخاب می شود یعنی aواحد یا ثابت شبکه نامیده می شود
a=b=cو زوایای آلفا و بتا و گاما برابر 90 درجه هستند
شاخص های میلر:
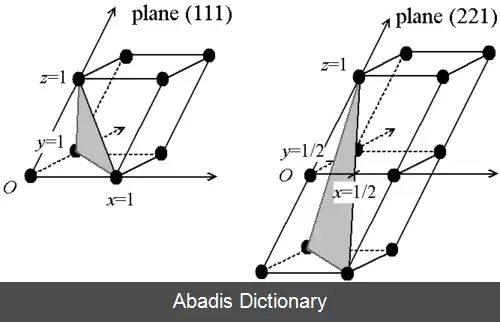
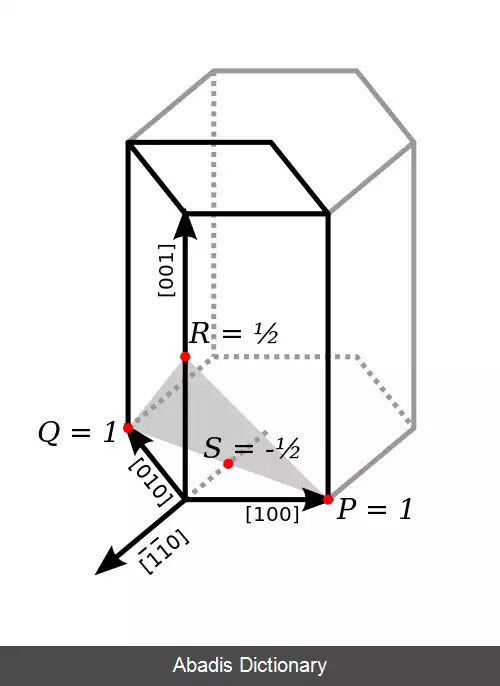
برای مشخص کردن یک صفحه کریستالوگرافی یعنی صفحه ای که از تعداد حداقل 3 اتم یک شبکه تشکیل شده است ابتدا محل تلاقی آن صفحه با محور های مختصات تعیین می شود سپس عکس این اعداد را بدست آورده و کوچک ترین مخرج مشترک اعداد را تعیین وهمگی را در آن عدد ضرب کرده و اعداد صحیح حاصل را بصورت ( h, k, l ) انتخاب میکنیم این فرم به معنای فرم اندیس میلر است
1 1 1
____ : _____ :____
X k l
به طور خاص، میلر یک گروه از شبکه های سطوح هموار را با سه عدد صحیح h, kوl مشخص می کنند. که به این ( hkℓ ) شکل نوشته می شوند، و نشان دهنده خانواده صفحات شبکه ( موازی ) ( از شبکه براوه داده شده ) متعامد به g h k ℓ = h b 1 + k b 2 + ℓ b 3 ، جایی که بردارهای انتقالی اولیه یا پایه شبکه متقابل برای شبکه براوه داده شده هستند. ( توجه داشته باشید که صفحه همیشه، متعامد به ترکیب خطی بردارهای شبکه مستقیم یا اصلی نیست. h a 1 + k a 2 + ℓ a 3 زیرا لازم نیست بردارهای شبکه مستقیم متعامد باشند )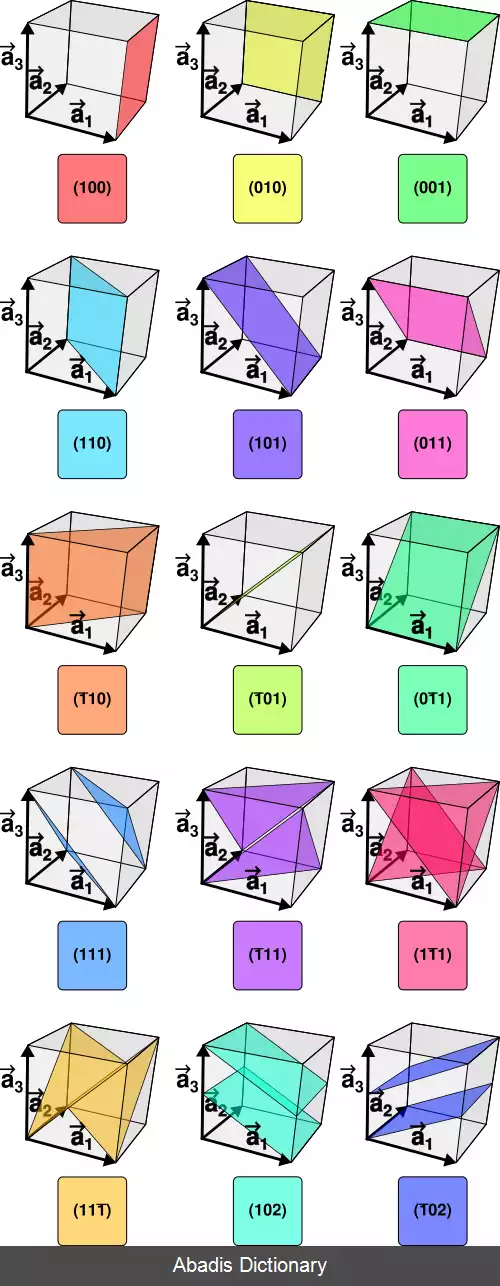
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفساختار کریستالی اتمی کریستال ها اغلب ناهمسان گر از لحاظ جهات کریستالی است که این غیر یکنواختی بر روی بعضی از خواص کریستال از جمله تغیر شکل پلاستیک تأثیر بسزایی دارد همچنین بعضی از خواص فیزیکی، تابع فاصله ی بین دو اتم مجاور در یک شبکه کریستالی و تعداد پیوند های بین آن ها است. بدین جهت برای تعیین موقعیت صفحات و جهات مختلف در هر شبکه کریستالی می توان از یک روش استاندارد شده استفاده کرد و این عمل به کمک اندیس میلر به صورت زیر انجام می گیرد. ابتدا یک سیستم محور مختصات فضایی که مبدا مختصات آن بر یکی از گوشه های سلول واحد منطبق و محور های آن در جهات مناسبی نسبت به محور های سلول واحد باشد انتخاب می کنیم ( جهات مناسب :جهاتی است که معمولاً موازی با محور های کریستال باشند ) به عنوان مثال در سیستم کریستالی مکعب و تتراگونال از یک سیستم محور مختصات عمود بر هم که مبدا مختصات آن منطبق یکی از گوشه های آن ومحور های مختصات
( x, y, z ) در امتداد سه ضلع عمود بر هم در آن گوشه سلول واحد باشد استفاده می کنیم به عنوان واحد اندازه گیری بر روی محور هاطول اضلاع سلول واحد کریستال یعنی ( a, b, C ) را انتخاب میکنیم در سیستم مکعب طول بردار ها برابر است و برابر واحد انتخاب می شود یعنی aواحد یا ثابت شبکه نامیده می شود
a=b=cو زوایای آلفا و بتا و گاما برابر 90 درجه هستند
شاخص های میلر:
برای مشخص کردن یک صفحه کریستالوگرافی یعنی صفحه ای که از تعداد حداقل 3 اتم یک شبکه تشکیل شده است ابتدا محل تلاقی آن صفحه با محور های مختصات تعیین می شود سپس عکس این اعداد را بدست آورده و کوچک ترین مخرج مشترک اعداد را تعیین وهمگی را در آن عدد ضرب کرده و اعداد صحیح حاصل را بصورت ( h, k, l ) انتخاب میکنیم این فرم به معنای فرم اندیس میلر است
1 1 1
____ : _____ :____
X k l
به طور خاص، میلر یک گروه از شبکه های سطوح هموار را با سه عدد صحیح h, kوl مشخص می کنند. که به این ( hkℓ ) شکل نوشته می شوند، و نشان دهنده خانواده صفحات شبکه ( موازی ) ( از شبکه براوه داده شده ) متعامد به g h k ℓ = h b 1 + k b 2 + ℓ b 3 ، جایی که بردارهای انتقالی اولیه یا پایه شبکه متقابل برای شبکه براوه داده شده هستند. ( توجه داشته باشید که صفحه همیشه، متعامد به ترکیب خطی بردارهای شبکه مستقیم یا اصلی نیست. h a 1 + k a 2 + ℓ a 3 زیرا لازم نیست بردارهای شبکه مستقیم متعامد باشند )




wiki: شاخص میلر
