لغت نامه دهخدا
فرهنگ فارسی
از نظر تشریح در زیست در استخوانهای جمجمه که از میان درزا کلیلی بر میان سر میرود تا بزاویه در زلامی و آنرا سهمی و سفودی نیز گویند
دانشنامه عمومی
در ریاضیات سَهمی ( به انگلیسی: Parabola ) مکان هندسی نقاطی از صفحه است که از یک خط و از یک نقطه هم فاصله هستند. این منحنی که شَلجَمی یا شَلغَمی[ ۱] هم نامیده می شود یکی از مقاطع مخروطی می باشد، زیرا از تقاطع یک صفحه و یک مخروط می تواند به وجود بیاید. [ ۲] سهمی و هذلولی دو مقطع مخروطی باز هستند و بیضی و دایره دو مقطع مخروطی بسته.
بنابر تقریظی از اراتوستن، سهمی را نخستین بار منایخموس ( ۳۸۰ — ۳۲۰ پ. م ) ، دوست نزدیک افلاطون، در تلاش برای حل تضعیف مکعب ( ساختن مکعبی که حجم آن دو برابر حجم یک مکعب مفروض است فقط با استفاده از خط کش و پرگار ) کشف کرد. آپولونیوس برای اولین بار نام «پارابول» ( یونانی: παραβολή، به معنای «کاربرد» ) [ الف] را بر روی سهمی گذاشت[ ۳] و اقلیدس ( حدود ۳۶۵–۲۷۵ پ. م ) بررسی دقیقی از ویژگی های سهمی ارائه کرد. [ ۴] پاپوس اسکندرانی ( حدود ۳۵۰ — ۲۹۰ پ. م ) مفهوم خط های هادی را برای نخستین بار بررسی کرد و نشان داد که هر منحنی نسبت ثابتی ( که بعدها به برون مرکزی معروف شد ) دارد و این نسبت ثابت برای همهٔ سهمی ها برابر ۱ است. [ ۵]
نام آپولونیوس ( اواخر قرن سوم — اوایل قرن دوم پیش از میلاد ) برای قرن ها پس از مرگ او با مطالعهٔ مقاطع مخروطی گره خورده بود. آپولونیوس اثر مهمش «مخروطات» را، که مشتمل بر هشت مقاله است، [ ۶] با مطالعهٔ مخروط آغاز می کند و پس از تعریف سه مقطع مخروطی ( سهمی، هذلولی، و بیضی ) ، به تعریف خط مماس آن ها می پردازد و سپس ثابت می کند که فاصلهٔ کانونی برای همهٔ نقاط روی یک بیضی ثابت است. [ ۷]
همزمان با حکومت مأمون در خراسان ( در قرن سوم هجری ) ، اخوان ثلاثهٔ بنوموسی دست به ترجمهٔ مخروطات آپولونیوس از یونانی به عربی زدند. بنوموسی فقط نسخه ای ناقص از مخروطات را در اختیار داشتند و مقاطع مخروطی در زمان ایشان به دست فراموشی سپرده شده بود، بنابراین در فهم متن دچار مشکل بودند. اندکی بعد، یکی از اخوان ثلاثه به نام حسن نظریهٔ مقاطع استوانه ای را ابداع کرد که می توان آن را مقدمه ای ساده بر مقاطع مخروطی دانست. پس از درگذشت حسن، برادرش احمد در شام نسخه ای کامل تر از چهار فصل اول مخروطات را با شرح اوتوکیوس پیدا کرد و به کمک برادر دیگرش، محمد، و با استفاده از دو نسخهٔ موجود و نظریهٔ حسن، موفق شد نظریات آپولونیوس را دریابد. احمد و محمد ترجمهٔ مقالهٔ اول تا چهارم مخروطات را به هلال حمصی و مقالهٔ پنجم تا هفتم آن را به ثابت بن قره سپردند و خود بازنگری نهایی ترجمه را عهده دار شدند. ترجمهٔ برادران بنوموسی از مقالات پنجم تا هفتم مخروطات تنها نسخهٔ باقی ماندهٔ این اثر است. [ ۶] ترجمهٔ آثار علمی به عربی اغلب نیازمند ابداع اصطلاحات فنی تازه بود و مترجمان آن ها، بر خلاف مترجمان لاتین، به ترانویسی عبارات یونانی اکتفا نکردند[ ب] و برای واژهٔ «پارابولی» اصطلاح «مکافی» را در نظر گرفتند که معنای آن را حفظ می کند[ پ] و هنوز در زبان عربی به بیضی «قطع ناقص» گفته می شود. [ ۶]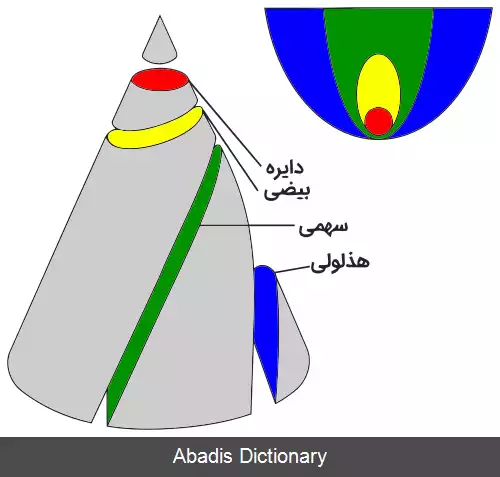




این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبنابر تقریظی از اراتوستن، سهمی را نخستین بار منایخموس ( ۳۸۰ — ۳۲۰ پ. م ) ، دوست نزدیک افلاطون، در تلاش برای حل تضعیف مکعب ( ساختن مکعبی که حجم آن دو برابر حجم یک مکعب مفروض است فقط با استفاده از خط کش و پرگار ) کشف کرد. آپولونیوس برای اولین بار نام «پارابول» ( یونانی: παραβολή، به معنای «کاربرد» ) [ الف] را بر روی سهمی گذاشت[ ۳] و اقلیدس ( حدود ۳۶۵–۲۷۵ پ. م ) بررسی دقیقی از ویژگی های سهمی ارائه کرد. [ ۴] پاپوس اسکندرانی ( حدود ۳۵۰ — ۲۹۰ پ. م ) مفهوم خط های هادی را برای نخستین بار بررسی کرد و نشان داد که هر منحنی نسبت ثابتی ( که بعدها به برون مرکزی معروف شد ) دارد و این نسبت ثابت برای همهٔ سهمی ها برابر ۱ است. [ ۵]
نام آپولونیوس ( اواخر قرن سوم — اوایل قرن دوم پیش از میلاد ) برای قرن ها پس از مرگ او با مطالعهٔ مقاطع مخروطی گره خورده بود. آپولونیوس اثر مهمش «مخروطات» را، که مشتمل بر هشت مقاله است، [ ۶] با مطالعهٔ مخروط آغاز می کند و پس از تعریف سه مقطع مخروطی ( سهمی، هذلولی، و بیضی ) ، به تعریف خط مماس آن ها می پردازد و سپس ثابت می کند که فاصلهٔ کانونی برای همهٔ نقاط روی یک بیضی ثابت است. [ ۷]
همزمان با حکومت مأمون در خراسان ( در قرن سوم هجری ) ، اخوان ثلاثهٔ بنوموسی دست به ترجمهٔ مخروطات آپولونیوس از یونانی به عربی زدند. بنوموسی فقط نسخه ای ناقص از مخروطات را در اختیار داشتند و مقاطع مخروطی در زمان ایشان به دست فراموشی سپرده شده بود، بنابراین در فهم متن دچار مشکل بودند. اندکی بعد، یکی از اخوان ثلاثه به نام حسن نظریهٔ مقاطع استوانه ای را ابداع کرد که می توان آن را مقدمه ای ساده بر مقاطع مخروطی دانست. پس از درگذشت حسن، برادرش احمد در شام نسخه ای کامل تر از چهار فصل اول مخروطات را با شرح اوتوکیوس پیدا کرد و به کمک برادر دیگرش، محمد، و با استفاده از دو نسخهٔ موجود و نظریهٔ حسن، موفق شد نظریات آپولونیوس را دریابد. احمد و محمد ترجمهٔ مقالهٔ اول تا چهارم مخروطات را به هلال حمصی و مقالهٔ پنجم تا هفتم آن را به ثابت بن قره سپردند و خود بازنگری نهایی ترجمه را عهده دار شدند. ترجمهٔ برادران بنوموسی از مقالات پنجم تا هفتم مخروطات تنها نسخهٔ باقی ماندهٔ این اثر است. [ ۶] ترجمهٔ آثار علمی به عربی اغلب نیازمند ابداع اصطلاحات فنی تازه بود و مترجمان آن ها، بر خلاف مترجمان لاتین، به ترانویسی عبارات یونانی اکتفا نکردند[ ب] و برای واژهٔ «پارابولی» اصطلاح «مکافی» را در نظر گرفتند که معنای آن را حفظ می کند[ پ] و هنوز در زبان عربی به بیضی «قطع ناقص» گفته می شود. [ ۶]






wiki: سهمی
دانشنامه آزاد فارسی
سَهْمی (parabola)
سهمی ساده
سهمی ساده
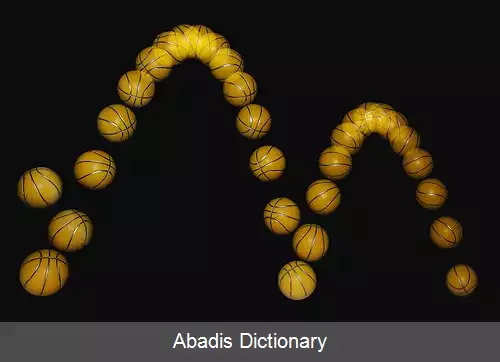
در ریاضیات، منحنی حاصل از تقاطع یک سطح مخروطی دوار با صفحه ای موازی با یکی از مولدهای سطح مخروطی، به قسمی که یک دامنۀ سطح را قطع کند. سهمی یکی از منحنی های خانوادۀ مقاطع مخروطی است. نمودارy = x۲، نشان دهندۀ سهمی است. این منحنی را همچنین می توان به صورت مسیر حرکت نقطه ای تعریف کرد که فاصلۀ آن از یک نقطۀ ثابت، با نام کانون، و یک خط راست ثابت، با نام هادی، همواره ثابت است. محور تقارن سهمی را محور سهمی می نامند. رأس سهمی محل تقاطع محور سهمی با سهمی و خروج از مرکز سهمی یک است. مسیر پرتابه ها در میدان گرانشی زمین، صرف نظر از اثر مقاومت هوا، تقریباً به شکل سهمی است. یک شکل فضایی متناظر با سهمی، سهمی وار دوّار است که از دوران سهمی حول محورش پدید می آید. بازتابگرِ چراغ جلو اتومبیل، آنتن بشقابی میکروموج و رادار، و تلسکوپ رادیویی معمولاً سهمی وار ساخته می شوند، زیرا اگر منبع تابش نور یا موج رادیویی در کانون یک بازتابگر سهمی وار قرار داده شود، پرتوها پس از برخورد با سهمی وار به موازات محور آن باز می تابند. نیز ← سهمی وار
سهمی ساده
سهمی ساده
در ریاضیات، منحنی حاصل از تقاطع یک سطح مخروطی دوار با صفحه ای موازی با یکی از مولدهای سطح مخروطی، به قسمی که یک دامنۀ سطح را قطع کند. سهمی یکی از منحنی های خانوادۀ مقاطع مخروطی است. نمودارy = x۲، نشان دهندۀ سهمی است. این منحنی را همچنین می توان به صورت مسیر حرکت نقطه ای تعریف کرد که فاصلۀ آن از یک نقطۀ ثابت، با نام کانون، و یک خط راست ثابت، با نام هادی، همواره ثابت است. محور تقارن سهمی را محور سهمی می نامند. رأس سهمی محل تقاطع محور سهمی با سهمی و خروج از مرکز سهمی یک است. مسیر پرتابه ها در میدان گرانشی زمین، صرف نظر از اثر مقاومت هوا، تقریباً به شکل سهمی است. یک شکل فضایی متناظر با سهمی، سهمی وار دوّار است که از دوران سهمی حول محورش پدید می آید. بازتابگرِ چراغ جلو اتومبیل، آنتن بشقابی میکروموج و رادار، و تلسکوپ رادیویی معمولاً سهمی وار ساخته می شوند، زیرا اگر منبع تابش نور یا موج رادیویی در کانون یک بازتابگر سهمی وار قرار داده شود، پرتوها پس از برخورد با سهمی وار به موازات محور آن باز می تابند. نیز ← سهمی وار
wikijoo: سهمی
مترادف ها
سهمی، هادی، مدیره، خط راهنما
تند، سرتیز، پیکانی، تیر مانند، تیردار، سهمی
سهمی، شبیه سهم یا تیر و کمان، وابسته به درز سهمی جمجمه
سهمی، نیزه ای، تبرزینی، سه گوش و نوک تیز
سهمی، شبیه تیر
پیشنهاد کاربران
منبع. عکس فرهنگ پاشنگ
واژه ی سهمی از ریشه ی واژه ی سهم و ی فارسی هست
زبان های ترکی�در چند مرحله بر�زبان فارسی�تأثیر گذاشته است. نخستین تأثیر زبان ترکی بر پارسی، در زمان حضور سربازان تُرک در ارتش�سامانیان�روی داد. پس از آن، در زمان فرمان روایی�غزنویان، �سلجوقیان�و پس از�حملهٔ مغول، تعداد بیشتری�وام واژهٔ�ترکی به زبان فارسی راه یافت؛ اما بیشترین راه یابی واژه های ترکی به زبان فارسی در زمان فرمانروایی�صفویان، که ترکمانان�قزلباش�در تأسیس آن نقش اساسی داشتند، و�قاجاریان�بر ایران بود.
... [مشاهده متن کامل]
• منابع ها. تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. اول و دوم، انتشارات ققنوس، ۱۳۷۴
• تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. سوم، انتشارات بدیهه، ۱۳۷۴
• حسن بیگ روملو، �احسن التواریخ� ( ۲ جلد ) ، به تصحیح�عبدالحسین نوایی، بنگاه ترجمه و نشر کتاب، ۱۳۴۹. ( مصحح در پایان جلد اول شرح مفصل و سودمندی از فهرست لغات�ترکی�و�مغولی�رایج در متون فارسی از سده هفتم به بعد را نوشته است )
• فرهنگ فارسی، محمد معین، انتشارات امیر کبیر، تهران، ۱۳۷۵
• غلط ننویسیم، ابوالحسن نجفی، مرکز نشر دانشگاهی، تهران، ۱۳۸۶
• فرهنگ کوچک زبان پهلوی، دیوید نیل مکنزی، ترجمه مهشید فخرایی، پژوهشگاه علوم انسانی و مطالعات فرهنگی، تهران، ۱۳۷۹




واژه ی سهمی از ریشه ی واژه ی سهم و ی فارسی هست
زبان های ترکی�در چند مرحله بر�زبان فارسی�تأثیر گذاشته است. نخستین تأثیر زبان ترکی بر پارسی، در زمان حضور سربازان تُرک در ارتش�سامانیان�روی داد. پس از آن، در زمان فرمان روایی�غزنویان، �سلجوقیان�و پس از�حملهٔ مغول، تعداد بیشتری�وام واژهٔ�ترکی به زبان فارسی راه یافت؛ اما بیشترین راه یابی واژه های ترکی به زبان فارسی در زمان فرمانروایی�صفویان، که ترکمانان�قزلباش�در تأسیس آن نقش اساسی داشتند، و�قاجاریان�بر ایران بود.
... [مشاهده متن کامل]
• منابع ها. تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. اول و دوم، انتشارات ققنوس، ۱۳۷۴
• تاریخ ادبیات ایران، ذبیح الله صفا، خلاصه ج. سوم، انتشارات بدیهه، ۱۳۷۴
• حسن بیگ روملو، �احسن التواریخ� ( ۲ جلد ) ، به تصحیح�عبدالحسین نوایی، بنگاه ترجمه و نشر کتاب، ۱۳۴۹. ( مصحح در پایان جلد اول شرح مفصل و سودمندی از فهرست لغات�ترکی�و�مغولی�رایج در متون فارسی از سده هفتم به بعد را نوشته است )
• فرهنگ فارسی، محمد معین، انتشارات امیر کبیر، تهران، ۱۳۷۵
• غلط ننویسیم، ابوالحسن نجفی، مرکز نشر دانشگاهی، تهران، ۱۳۸۶
• فرهنگ کوچک زبان پهلوی، دیوید نیل مکنزی، ترجمه مهشید فخرایی، پژوهشگاه علوم انسانی و مطالعات فرهنگی، تهران، ۱۳۷۹




گُریزه
سهمی به خمی گفته می شود که فاصله هر نقطه آن از یک نقطه ثابت به نام کانونو یک خط به نام هادی مقدار ثابتی باشد. در چنین حالتی گریز از مرکز این خم در حد آستانه است و خم از کانون دور می شود. از این رو می توان چنین گفت که خم می خواهد از کانون بگریزد و شدت این گریز در آستانه گریز است.
سهمی به خمی گفته می شود که فاصله هر نقطه آن از یک نقطه ثابت به نام کانونو یک خط به نام هادی مقدار ثابتی باشد. در چنین حالتی گریز از مرکز این خم در حد آستانه است و خم از کانون دور می شود. از این رو می توان چنین گفت که خم می خواهد از کانون بگریزد و شدت این گریز در آستانه گریز است.
