رنگ آمیزی گراف. در نظریه گراف، رنگ آمیزی گراف یکی از حالت های خاص مسئله های برچسب گذاری گراف است. رویکرد کلی آن استفاده از نظیر کردن رنگهایی به یالها یا راس هاست که این رنگ آمیزی محدودیت خاصی را رعایت کند. در ساده ترین حالت، رنگ آمیزی ای مورد نظر است که در آن هیچ دو راس مجاوری هم رنگ نباشند ( رنگ آمیزی راسها ) . علاوه بر آن رنگ آمیزی یالها به همین صورت تعریف می شود.
رنگ آمیزی گراف کاربردهای زیادی در زمینه های عملی و تئوری گوناگون دارد. علاوه بر مسئله های کلاسیک تعریف شده در این زمینه، با در نظر گرفتن محدودیت های مختلفی روی نوع گرافها، روی روش رنگ آمیزی و حتی تعداد و رنگ عناصر گراف مسئله های متنوعی با کاربردهای وسیع در صنعت و علوم تعریف و حل می شود. با وجود اینکه این مسئله از نظر علمی هنوز در حال رشد و بررسی بیشتر می باشد.
اولین نتیجه های بدست آمده در مورد رنگ آمیزی گراف از تلاش های انجام شده بر روی گراف های مسطح برای حل مسئله رنگ آمیزی نقشه بدست آمد. در آن زمان فرانسیس گوتری ادعا کرد که رنگ آمیزی نقشه ایالت های مختلف بریتانیا روی نقشه، به طوری که هیچ دو ایالت مجاوری همرنگ نشوند، می تواند با ۴ رنگ انجام شود ( شرط کافی ) . برادر گوتری این مسئله را برای معلم ریاضی خود آگوستوس دو مورگان، در کالج دانشگاهی فرستاد. دو مورگان، این مسئله را در سال ۱۸۵۲ میلادی در نامه ای که به ویلیام همیلتون نوشت مطرح کرد. در سال ۱۸۷۹ آرتور کیلی این مسئله را در انجمن ریاضی شهر لندن مطرح کرد. در همان سال آلفرد کمپ، نتایج بدست آمده را منتشر کرد و برای یک دهه تصور می شد این مسئله حل شده است. برای تلاش های کمپ در این زمینه او به عنوان یکی از اعضای جامعه سلطنتی و بعدها به عنوان ریاست انجمن ریاضی شهر لندن انتخاب شد.
در سال1890 Heawood، ادعا کرد که استدلال کمپ اشتباه بوده است و اثبات این مسئله را برای ۵ رنگ منتشر کرد. در قرن معاصر او تلاش های زیادی برای اثبات روش های رنگ آمیزی نقشه با تعداد ۴ رنگ صورت گرفت که در نهایت در سال ۱۹۷۶ توسط Kenneth Appel وWolfgang Haken این مسئله به کمک ایده های خود Heawood و کمپ انجام شد که در آن زمان به دلیل استفاده از کامپیوتر برای اثبات مسئله، شدیداً مورد قبول واقع نشد.
رنگ آمیزی گراف از اوایل دهه ۷۰ به عنوان یک مسئله الگوریتمی مورد بررسی قرار گرفته است، به طوری که جزء یکی از ۲۱ مسئله NP - Complete که Karp معرفی کرد قرار گرفته.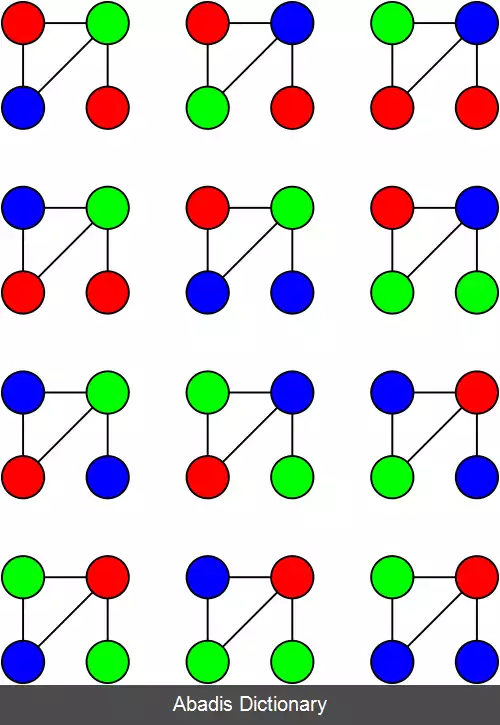
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفرنگ آمیزی گراف کاربردهای زیادی در زمینه های عملی و تئوری گوناگون دارد. علاوه بر مسئله های کلاسیک تعریف شده در این زمینه، با در نظر گرفتن محدودیت های مختلفی روی نوع گرافها، روی روش رنگ آمیزی و حتی تعداد و رنگ عناصر گراف مسئله های متنوعی با کاربردهای وسیع در صنعت و علوم تعریف و حل می شود. با وجود اینکه این مسئله از نظر علمی هنوز در حال رشد و بررسی بیشتر می باشد.
اولین نتیجه های بدست آمده در مورد رنگ آمیزی گراف از تلاش های انجام شده بر روی گراف های مسطح برای حل مسئله رنگ آمیزی نقشه بدست آمد. در آن زمان فرانسیس گوتری ادعا کرد که رنگ آمیزی نقشه ایالت های مختلف بریتانیا روی نقشه، به طوری که هیچ دو ایالت مجاوری همرنگ نشوند، می تواند با ۴ رنگ انجام شود ( شرط کافی ) . برادر گوتری این مسئله را برای معلم ریاضی خود آگوستوس دو مورگان، در کالج دانشگاهی فرستاد. دو مورگان، این مسئله را در سال ۱۸۵۲ میلادی در نامه ای که به ویلیام همیلتون نوشت مطرح کرد. در سال ۱۸۷۹ آرتور کیلی این مسئله را در انجمن ریاضی شهر لندن مطرح کرد. در همان سال آلفرد کمپ، نتایج بدست آمده را منتشر کرد و برای یک دهه تصور می شد این مسئله حل شده است. برای تلاش های کمپ در این زمینه او به عنوان یکی از اعضای جامعه سلطنتی و بعدها به عنوان ریاست انجمن ریاضی شهر لندن انتخاب شد.
در سال1890 Heawood، ادعا کرد که استدلال کمپ اشتباه بوده است و اثبات این مسئله را برای ۵ رنگ منتشر کرد. در قرن معاصر او تلاش های زیادی برای اثبات روش های رنگ آمیزی نقشه با تعداد ۴ رنگ صورت گرفت که در نهایت در سال ۱۹۷۶ توسط Kenneth Appel وWolfgang Haken این مسئله به کمک ایده های خود Heawood و کمپ انجام شد که در آن زمان به دلیل استفاده از کامپیوتر برای اثبات مسئله، شدیداً مورد قبول واقع نشد.
رنگ آمیزی گراف از اوایل دهه ۷۰ به عنوان یک مسئله الگوریتمی مورد بررسی قرار گرفته است، به طوری که جزء یکی از ۲۱ مسئله NP - Complete که Karp معرفی کرد قرار گرفته.


wiki: رنگ آمیزی گراف
