خروج از مرکز مداری[ ۱] ( به انگلیسی:Orbital eccentricity ) پارامتری است که توسط آن مقدار تفاوت مدار یک جرم به دور جرمی دیگر از نظر انحراف از یک دایرهٔ کامل بودن را تعیین می کند. مقدار صفر این پارامتر دایرهٔ کامل بودن یک مدار را نشان می دهد، مقادیر بین صفر و ۱ یک مدار بیضی شکل، و مقدار ۱ نمایان گر یک مدار سهموی فرار است و همچنین مقادیر بیشتر از ۱ یک مدار هذلولی است.
در مکانیک سماوی و طبق قانون اول کپلر مدار سیارات دایره نیست و بیضی است که خورشید به عنوان عامل گرانشی در یکی از کانون های آن قرار گرفته؛ برای تمایز مقاطع مخروطی از یکدیگر از کمیتی استفاده می شود که به آن خروج از مرکز ( انگلیسی: eccentricity ) می گویند که با علامت ( e ) نشان داده می شود:
• برای مدار دایره: e = 0 {\displaystyle e=0\, \!}
• برای مدار بیضی: 0 < e < 1 {\displaystyle 0< e< 1\, \!} ،
• برای مدار سهموی: e = 1 {\displaystyle e=1\, \!} ،
• مدار هذلولوی: e > 1 {\displaystyle e> 1\, \!} .
خروج از مرکز را می توان از رابطه زیر به دست آورد:
که:
• e {\displaystyle \mathbf {e} \, \!} خروج از مرکز برداری است.
برای مدارها می توان از فرمول زیر و با استفاده از فواصل اوج و حضیض مداری:
• r a {\displaystyle r_{a}\, \!} فاصلهٔ اوج مداری، [ ۲]
• r p {\displaystyle r_{p}\, \!} فاصلهٔ حضیض[ ۳] مداریست.
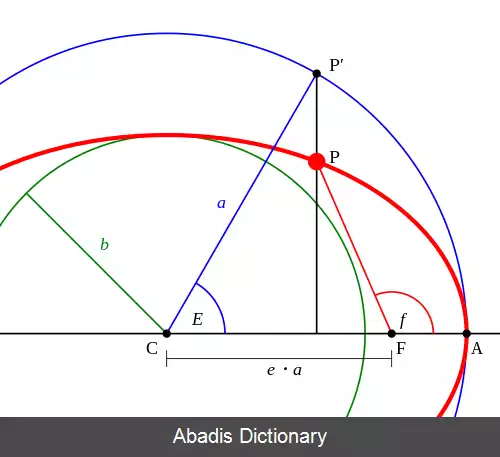
البته دو کمیت اخیر را نباید با نیم محور کوچک[ ۴] و نیم محور بزرگ[ ۵] بیضی اشتباه گرفت که نسبت به مرکز بیضی تعریف می شوند، حال آنکه نقاط اوج و حضیض مداری نسبت به کانون بیضی یا محل قرارگیری تقریبی خورشید تعریف می شوند[ ۶] دراین خصوص لطفاً به شکل مقابل مراجعه کنید. البته می توان خروج از مرکز هر بیضی را هم با کمک این کمیتها و روابط زیر محاسبه کرد:
که در آن a نیم محور بزرگ، b نیم محور کوچک و c فاصلهٔ هر کانون بیضی از مرکز بیضی است. روابط زیر ارتباط بین فواصل اوج و حضیض مداری و اندازهٔ نیم محور بزرگ را در بیضی نشان می دهند:
رابطه زیر نشان می دهد که چگونه با در دست داشتن خروج ار مرکز مداری می توان مسیر مدار هر سیاره را مشخص کرد:
این رابطه با توجه به توضیحی که در بخش قبل داده شد می تواند بسته به مقدار خروج از مرکز مدارهایی به شکل یک مقطع مخروطی را توصیف کند، در این رابطه پارامتر f زاویهٔ موسوم به ناهنجار حقیقی[ ۷] که رأس آن کانون یا محل قرارگیری جرم مرکزی است و دو انتهای آن بین نقطهٔ حضیض مداری[ ۸] و نقطه ای از مدار است که سیاره ( ماهواره ) در آنجا قرار می گیرد. ( شکل مقابل )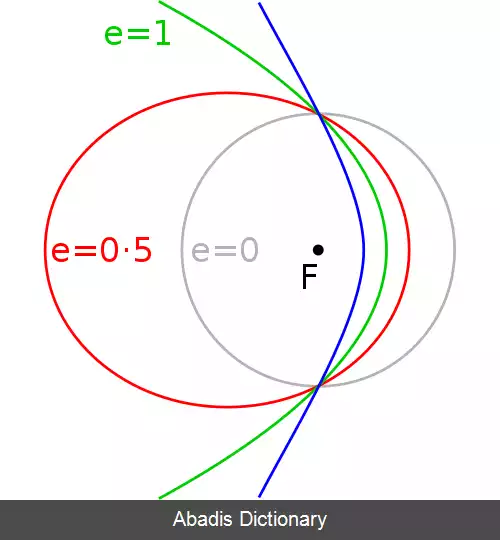
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر مکانیک سماوی و طبق قانون اول کپلر مدار سیارات دایره نیست و بیضی است که خورشید به عنوان عامل گرانشی در یکی از کانون های آن قرار گرفته؛ برای تمایز مقاطع مخروطی از یکدیگر از کمیتی استفاده می شود که به آن خروج از مرکز ( انگلیسی: eccentricity ) می گویند که با علامت ( e ) نشان داده می شود:
• برای مدار دایره: e = 0 {\displaystyle e=0\, \!}
• برای مدار بیضی: 0 < e < 1 {\displaystyle 0< e< 1\, \!} ،
• برای مدار سهموی: e = 1 {\displaystyle e=1\, \!} ،
• مدار هذلولوی: e > 1 {\displaystyle e> 1\, \!} .
خروج از مرکز را می توان از رابطه زیر به دست آورد:
که:
• e {\displaystyle \mathbf {e} \, \!} خروج از مرکز برداری است.
برای مدارها می توان از فرمول زیر و با استفاده از فواصل اوج و حضیض مداری:
• r a {\displaystyle r_{a}\, \!} فاصلهٔ اوج مداری، [ ۲]
• r p {\displaystyle r_{p}\, \!} فاصلهٔ حضیض[ ۳] مداریست.
البته دو کمیت اخیر را نباید با نیم محور کوچک[ ۴] و نیم محور بزرگ[ ۵] بیضی اشتباه گرفت که نسبت به مرکز بیضی تعریف می شوند، حال آنکه نقاط اوج و حضیض مداری نسبت به کانون بیضی یا محل قرارگیری تقریبی خورشید تعریف می شوند[ ۶] دراین خصوص لطفاً به شکل مقابل مراجعه کنید. البته می توان خروج از مرکز هر بیضی را هم با کمک این کمیتها و روابط زیر محاسبه کرد:
که در آن a نیم محور بزرگ، b نیم محور کوچک و c فاصلهٔ هر کانون بیضی از مرکز بیضی است. روابط زیر ارتباط بین فواصل اوج و حضیض مداری و اندازهٔ نیم محور بزرگ را در بیضی نشان می دهند:
رابطه زیر نشان می دهد که چگونه با در دست داشتن خروج ار مرکز مداری می توان مسیر مدار هر سیاره را مشخص کرد:
این رابطه با توجه به توضیحی که در بخش قبل داده شد می تواند بسته به مقدار خروج از مرکز مدارهایی به شکل یک مقطع مخروطی را توصیف کند، در این رابطه پارامتر f زاویهٔ موسوم به ناهنجار حقیقی[ ۷] که رأس آن کانون یا محل قرارگیری جرم مرکزی است و دو انتهای آن بین نقطهٔ حضیض مداری[ ۸] و نقطه ای از مدار است که سیاره ( ماهواره ) در آنجا قرار می گیرد. ( شکل مقابل )



wiki: خروج از مرکز مداری
