خاصیت جابه جایی ( به انگلیسی: Commutative ) در علم ریاضیات، یک خاصیت برای یک عمل دوتایی است، که تغییر ترتیب عملوندها بر روی نتیجه تأثیر نداشته باشد. خاصیت جابجایی، خاصیتی بنیادین برای بسیاری از عمل های دوتایی می باشد و بسیاری از اثبات های ریاضیاتی به آن بستگی دارد. این همان خاصیت آشنای "۳+۴=۴+۳" یا "۲×۵=۵×۲" است. ازین خاصیت می توان در حالات پیشرفته تر نیز استفاده کرد. برخی از عمل های دوتایی چون تقسیم و تفاضل خاصیت جابجایی ندارند ( مثلاً "۳ - ۵≠۵ - ۳" ) ؛ چنین عمل هایی جابجایی نیستند، لذا به آن ها عمل های ناجابجایی می گویند. این ایده که عملیات ساده ای چون ضرب و جمع اعداد جابجایی هستند، سال ها به صورت ضمنی و پنهان فرض می شد. لذا، این خاصیت تا قرن ۱۹ میلادی به صورت آشکار مطرح نشد، در این زمان بود که ریاضیات شروع به صوری سازی این مفهوم کرد. [ ۱] [ ۲] برای روابط دوتایی هم خاصیتی مشابه به نام خاصیت تقارنی وجود دارد، روابطی که این خاصیت را دارند، ترتیب عملوندها برایشان اهمیتی ندارد. مثالی از روابط دوتایی متقارن، رابطه تساوی است که معمولاً آن را با = نشان می دهند. علت متقارن بودن این رابطه این است که در برابری دو شیء، ترتیب قرارگیریشان در دو سمت نماد تساوی اهمیتی ندارد. [ ۳]
عبارت «جابه جایی پذیر» در چند مورد مشابه کاربرد دارد. [ ۴] [ ۵]
۱. یک عمل دوتایی تحت عمل گر ∗ در مجموعهٔ S جابه جایی پذیر است اگر:
۲. کاربرد دیگر می گوید که x جابه جا می شود با y تحت ∗ اگر:
۳. یک تابع دو متغیره مانند f:A×A → B دارای خاصیت جابه جایی است، اگر:
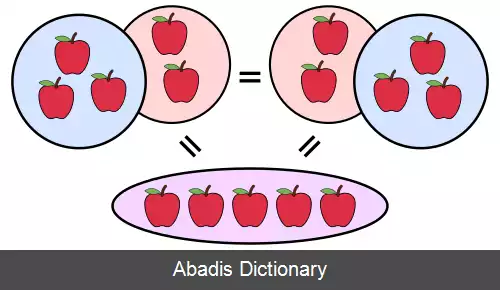
• جمع و ضرب در اکثر سیستم اعداد، به ویژه بین اعداد طبیعی، اعداد صحیح، اعداد گویا، اعداد حقیقی و اعداد مختلط، رابطه جابجایی برقرار است. این ویژگی همچنین در هر میدانی صدق می کند.
• عمل جمع برداری در هر جبری جابجایی پذیر است.
• اتحاد و اشتراک عملیات های جابجایی پذیر روی مجموعه ها هستند.
• عملیات های منطقی "و" و "یا" نیز ارتباطی جابجایی پذیر هستند.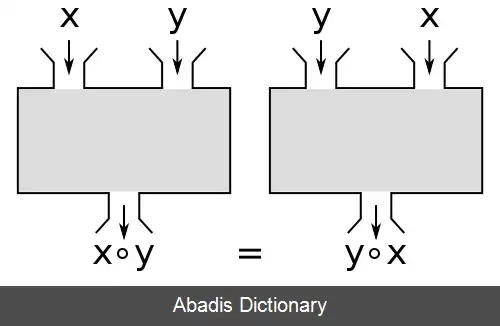
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفعبارت «جابه جایی پذیر» در چند مورد مشابه کاربرد دارد. [ ۴] [ ۵]
۱. یک عمل دوتایی تحت عمل گر ∗ در مجموعهٔ S جابه جایی پذیر است اگر:
۲. کاربرد دیگر می گوید که x جابه جا می شود با y تحت ∗ اگر:
۳. یک تابع دو متغیره مانند f:A×A → B دارای خاصیت جابه جایی است، اگر:
• جمع و ضرب در اکثر سیستم اعداد، به ویژه بین اعداد طبیعی، اعداد صحیح، اعداد گویا، اعداد حقیقی و اعداد مختلط، رابطه جابجایی برقرار است. این ویژگی همچنین در هر میدانی صدق می کند.
• عمل جمع برداری در هر جبری جابجایی پذیر است.
• اتحاد و اشتراک عملیات های جابجایی پذیر روی مجموعه ها هستند.
• عملیات های منطقی "و" و "یا" نیز ارتباطی جابجایی پذیر هستند.


wiki: خاصیت جابه جایی
