توزیع پذیری یا پخش پذیری خاصیتی در ریاضیات است که برای عملی دوتایی تعریف می شود.
فرض کنیم ∗ و ∘ اعمالی دوتایی در مجموعه ناتهی A باشند. عمل ∗ را نسبت به ∘ توزیع پذیر خوانیم هرگاه به ازای هر a و b و c از A، دو برابری زیر برقرار باشند:
برابری نخست را توزیع پذیری از چپ و برابری دوم را توزیع پذیری از راست می نامیم.
• در مجموعه های اعداد حقیقی و مختلط عمل ضرب نسبت به جمع و تفریق توزیع پذیر است. یعنی همواره
• اعمال اجتماع و اشتراک در مجموعه ها نسبت به یکدیگر توزیع پذیرند. یعنی برای هر سه مجموعه دلخواه A و B و C،
• ضرب دکارتی نسبت به اجتماع و اشتراک توزیع پذیر است. اگر A و B و C را سه مجموعه بگیریم، آنگاه
• حاصلضرب دکارتی نسبت به عمل متممگیری توزیع پذیر است.
• در اعداد اصلی عمل ضرب نسبت به عمل جمع توزیع پذیر است.
• در منطق، و ( ∧ ) نسبت به یا ( ∨ ) توزیع پذیر است و برعکس. اگر فرض کنیم P و Q و R گزاره هستند، آنگاه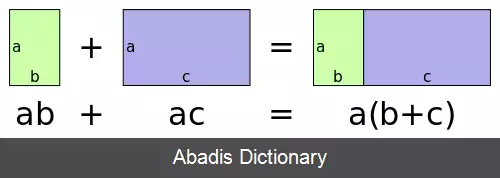
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنیم ∗ و ∘ اعمالی دوتایی در مجموعه ناتهی A باشند. عمل ∗ را نسبت به ∘ توزیع پذیر خوانیم هرگاه به ازای هر a و b و c از A، دو برابری زیر برقرار باشند:
برابری نخست را توزیع پذیری از چپ و برابری دوم را توزیع پذیری از راست می نامیم.
• در مجموعه های اعداد حقیقی و مختلط عمل ضرب نسبت به جمع و تفریق توزیع پذیر است. یعنی همواره
• اعمال اجتماع و اشتراک در مجموعه ها نسبت به یکدیگر توزیع پذیرند. یعنی برای هر سه مجموعه دلخواه A و B و C،
• ضرب دکارتی نسبت به اجتماع و اشتراک توزیع پذیر است. اگر A و B و C را سه مجموعه بگیریم، آنگاه
• حاصلضرب دکارتی نسبت به عمل متممگیری توزیع پذیر است.
• در اعداد اصلی عمل ضرب نسبت به عمل جمع توزیع پذیر است.
• در منطق، و ( ∧ ) نسبت به یا ( ∨ ) توزیع پذیر است و برعکس. اگر فرض کنیم P و Q و R گزاره هستند، آنگاه

wiki: خاصیت توزیع پذیری
