حوزه ایده آل اصلی. در ریاضیات، حوزه ایده آل اصلی ( به انگلیسی: Principal Ideal Domain ) ، یا PID، حوزه صحیحی است که هر ایده آلش اصلی باشد، یعنی، بتوان آن را با یک عنصر تولید کرد. به طور کلی تر، حلقه ایده آل اصلی، حلقه ناصفر جابجایی است که ایده آل هایش اصلی باشند، گرچه که برخی مؤلفان ( مثل بورباکی ) به PID ها، حلقه های اصلی می گویند. تفاوت اصلی بینشان این است که حلقه ایده آل اصلی ممکن است دارای مقسوم علیه های صفر باشند، در حالی که حوزه ایده آل اصلی چنین عناصری ندارد.
ازینرو، حوزه های ایده آل اصلی، اشیائی اند که نسبت به تقسیم پذیری همچون اعداد صحیح رفتار می کنند: هر عنصر از PID دارای تجزیه یکتایی به عناصر اول اند ( بنابر این مشابه قضیه اساسی حساب هم در اینجا صادق است ) ؛ هر دو عنصر از یک PID دارای بزرگترین مقوم علیه مشترک است ( گرچه که ممکن است امکان پیدا کردنش با الگوریتم اقلیدس وجود نداشته باشد ) . اگر x و y دو عنصر از یک PID، و بدون مقسوم علیه مشترک باشند، آنگاه هر عنصر از PID را می توان به صورت ax+by نوشت.
حوزه های ایده آل اصلی نوتری، بسته صحیح، حوزه تجزیه یکتا و حوزه های ددکیند اند. تمام حوزه های اقلیدسی و تمام میدان ها، حوزه های ایده آل صحیح اند.
حوزه های ایده آل اصلی در زنجیره شمول زیر قرار دارند: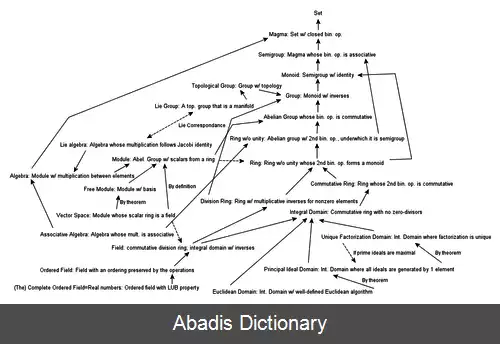
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفازینرو، حوزه های ایده آل اصلی، اشیائی اند که نسبت به تقسیم پذیری همچون اعداد صحیح رفتار می کنند: هر عنصر از PID دارای تجزیه یکتایی به عناصر اول اند ( بنابر این مشابه قضیه اساسی حساب هم در اینجا صادق است ) ؛ هر دو عنصر از یک PID دارای بزرگترین مقوم علیه مشترک است ( گرچه که ممکن است امکان پیدا کردنش با الگوریتم اقلیدس وجود نداشته باشد ) . اگر x و y دو عنصر از یک PID، و بدون مقسوم علیه مشترک باشند، آنگاه هر عنصر از PID را می توان به صورت ax+by نوشت.
حوزه های ایده آل اصلی نوتری، بسته صحیح، حوزه تجزیه یکتا و حوزه های ددکیند اند. تمام حوزه های اقلیدسی و تمام میدان ها، حوزه های ایده آل صحیح اند.
حوزه های ایده آل اصلی در زنجیره شمول زیر قرار دارند:

wiki: حوزه ایده آل اصلی
