ثابت ریاضی عددی خاص و معمولاً حقیقی است. ثابت ها در قسمت های مختلفی از ریاضیات مانند هندسه، نظریه اعداد، حساب دیفرانسیل و انتگرال و . . . ظاهر می شوند. برخی ثابت ها مانند عدد پی یا e برای ویژگی های یکتا و زمینه تاریخیشان مورد توجه ریاضی دان ها قرار دارند. ثابت های شناخته شده تر برای سال ها مورد مطالعه قرار گرفته اند و برای محاسبه مقدار آن ها تلاش های زیادی صورت گرفته است.
عدد π با مقدار تقریبی ۳٫۱۴۱۵۹، تعریف مشخصی در هندسه اقلیدسی دارد و آن نسبت محیط دایره به قطر آن است. اما ممکن است در جای های زیادی از ریاضیات دیده شود، مانند انتگرال گاوسی در آنالیز مختلط، ریشه های یک در نظریه اعداد یا توزیع کوشی در احتمالات. البته کاربرد آن تنها محدود به ریاضیات محض نیست و برای مثال در فیزیک در اصل عدم قطعیت، ثابت کیهان شناسی و قانون کولن ظاهر می شود.
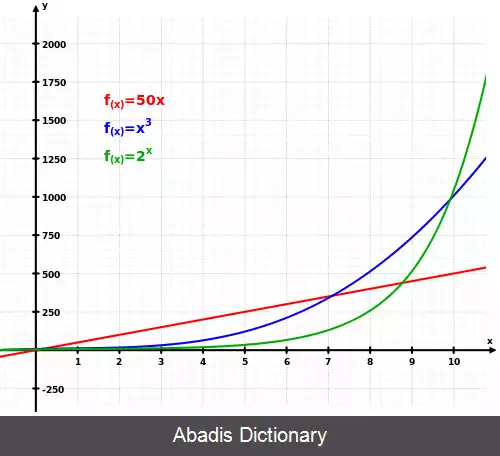
عدد e با مقدار تقریبی ۲٫۷۱۸۲۸ که با نام ثابت رشد نمایی نیز شناخته می شود، در بخش های مختلفی از ریاضی پدیدار می گردد. یکی از تعریف های که می توان برای آن ارائه کرد مقدار حد زیر است:
e = lim n → ∞ ( 1 + 1 n ) n
ثابت e کاربردهای زیادی دارد. به عنوان مثال در نظریه احتمال در توزیع نمایی پدیدار می گردد.
گاهی در حل معادله دیفرانسیل یا انتگرالی، جواب یکتا نیست و ممکن است بی نهایت جواب یافت شود که هرکدام تنها در عدد ثابتی با یکدیگر تفاوت داشته باشند. در اینگونه موارد آن اعداد را در حالت کلی با c نشان می دهیم که نمایندهٔ تمام آن هاست. به عنوان مثال پاسخ انتگرال نامعین ∫ cos x d x در میدان اعداد حقیقی، برابر با sin x + c است. در اینجا c نمایندهٔ تمام اعداد حقیقی است و در واقع به ازای هر عدد حقیقی یک جواب بدست می آید. چرا که مشتق sin x + c صرف نظر از اینکه c چه عددی باشد، همواره برابر cos x است.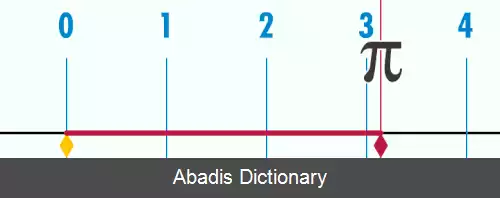
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفعدد π با مقدار تقریبی ۳٫۱۴۱۵۹، تعریف مشخصی در هندسه اقلیدسی دارد و آن نسبت محیط دایره به قطر آن است. اما ممکن است در جای های زیادی از ریاضیات دیده شود، مانند انتگرال گاوسی در آنالیز مختلط، ریشه های یک در نظریه اعداد یا توزیع کوشی در احتمالات. البته کاربرد آن تنها محدود به ریاضیات محض نیست و برای مثال در فیزیک در اصل عدم قطعیت، ثابت کیهان شناسی و قانون کولن ظاهر می شود.
عدد e با مقدار تقریبی ۲٫۷۱۸۲۸ که با نام ثابت رشد نمایی نیز شناخته می شود، در بخش های مختلفی از ریاضی پدیدار می گردد. یکی از تعریف های که می توان برای آن ارائه کرد مقدار حد زیر است:
e = lim n → ∞ ( 1 + 1 n ) n
ثابت e کاربردهای زیادی دارد. به عنوان مثال در نظریه احتمال در توزیع نمایی پدیدار می گردد.
گاهی در حل معادله دیفرانسیل یا انتگرالی، جواب یکتا نیست و ممکن است بی نهایت جواب یافت شود که هرکدام تنها در عدد ثابتی با یکدیگر تفاوت داشته باشند. در اینگونه موارد آن اعداد را در حالت کلی با c نشان می دهیم که نمایندهٔ تمام آن هاست. به عنوان مثال پاسخ انتگرال نامعین ∫ cos x d x در میدان اعداد حقیقی، برابر با sin x + c است. در اینجا c نمایندهٔ تمام اعداد حقیقی است و در واقع به ازای هر عدد حقیقی یک جواب بدست می آید. چرا که مشتق sin x + c صرف نظر از اینکه c چه عددی باشد، همواره برابر cos x است.


wiki: ثابت ریاضی
