در نظریه آمار و احتمال ، توزیع یکنواخت گسسته یک توزیع احتمال گسسته است که احتمال مشاهده تعداد محدودی پیشامد را یکسان گزارش می دهد. احتمال هر کدام از n پیشامد قابل مشاهده ای که از این توزیع پیروی می کنند، برابر با 1 / n است.
مثالی از این توزیع، انداختن تاس سالم است، که تمام شش وجه آن ( پیشامد های قابل مشاهده ) با احتمالی برابر 1 / 6 ظاهر می شوند.
برای یک مجموعه n عضوی، با فرض هم شانس بودن پیشامد ها، جمع احتمال تمام پیشامد ها خواهد بود: P ( S ) = P ( ⋃ i = 1 n E i ) = ∑ k = 1 n P ( E i ) = n P ( E i ) طبق تعریف داریم P ( S ) = 1 . پس : P ( S ) = n P ( E i ) = 1 ⟹ P ( E i ) = 1 / n توزیع محدود به بازه روش مرسومی از استفاده توزیع گسسته یکنواخت ، انتخاب اعداد صحیح در بازه ( a , b ∈ Z ) به عنوان فضای نمونه است. در این حالت داریم :
توزیع احتمال :
P ( X ) = { 1 / ( a − b ) if X is in 0 Otherwise
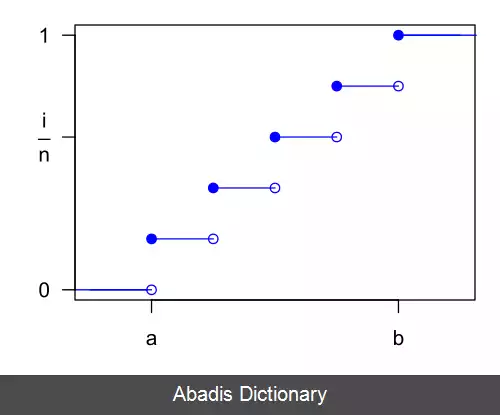
توزیع احتمال تجمعی :
C ( X ) = { 0 X < a ⌊ X ⌋ − a + 1 b − a + 1 , X in 1 X > b
امید ریاضی :
E ( X ) = ∑ x = a b x P ( x ) = 1 / ( b − a + 1 ) ∑ x = a b x
= 1 / ( b − a + 1 ) ( ( b + a ) ( b − a + 1 ) / 2 )
= ( b + a ) / 2
واریانس :
V ( X ) = ∑ x = a b P ( x ) ( x − E ( X ) ) 2
= 1 / ( b − a + 1 ) ) ( ∑ x = a b ( x − b + a 2 ) 2 )
= ( b − a ) 2 12
توزیع گسسته یکنواخت در بسیاری از تقریب ها و مشاهدات ظاهر می شوند. مشاهده این توزیع ( به طور شهودی ) نشان دهنده نبود تفاوت مؤثر بین پیشامدها است. با استفاده از اصل حداکثر انتروپی می توان اثبات کرد وقتی چیزی جز مقادیر قابل مشاهده ( فضای نمونه ) نمی دانیم، باید احتمال تمام آن ها را برابر در نظر بگیریم. [ ۱]
اما مثال هایی وجود دارد که علی رغم نبود تفاوت میان حالات ( حداقل در نگاه اول ) ، توزیع رخدادها از توزیع یکنواخت بسیار متفاوت است. به طور مثال می توان یه قانون بنفورد اشاره کرد.
یک سیستم که خروجی هایش به طور مطلق از توزیع یکنواخت گسسته پیروی می کند کاریرد های فراوانی در نمونه برداری آماری، رمزنگاری، قمار و . . . دارد اما ساختن چنین ماشینی کار بسیار سختی است. امروزه از روش هایی مثل الگوریتم های کامپیوتری و دریافت تابش کیهانی برای تولید این خروجی ها استفاده می شود.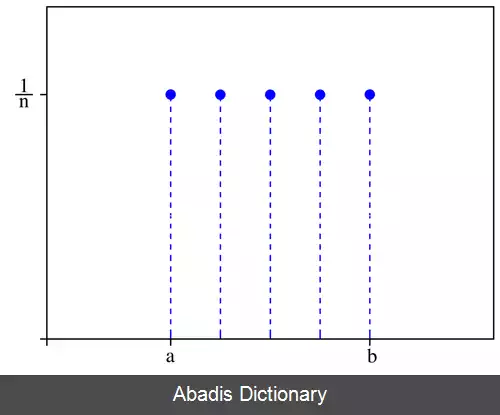
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمثالی از این توزیع، انداختن تاس سالم است، که تمام شش وجه آن ( پیشامد های قابل مشاهده ) با احتمالی برابر 1 / 6 ظاهر می شوند.
برای یک مجموعه n عضوی، با فرض هم شانس بودن پیشامد ها، جمع احتمال تمام پیشامد ها خواهد بود: P ( S ) = P ( ⋃ i = 1 n E i ) = ∑ k = 1 n P ( E i ) = n P ( E i ) طبق تعریف داریم P ( S ) = 1 . پس : P ( S ) = n P ( E i ) = 1 ⟹ P ( E i ) = 1 / n توزیع محدود به بازه روش مرسومی از استفاده توزیع گسسته یکنواخت ، انتخاب اعداد صحیح در بازه ( a , b ∈ Z ) به عنوان فضای نمونه است. در این حالت داریم :
توزیع احتمال :
P ( X ) = { 1 / ( a − b ) if X is in 0 Otherwise
توزیع احتمال تجمعی :
C ( X ) = { 0 X < a ⌊ X ⌋ − a + 1 b − a + 1 , X in 1 X > b
امید ریاضی :
E ( X ) = ∑ x = a b x P ( x ) = 1 / ( b − a + 1 ) ∑ x = a b x
= 1 / ( b − a + 1 ) ( ( b + a ) ( b − a + 1 ) / 2 )
= ( b + a ) / 2
واریانس :
V ( X ) = ∑ x = a b P ( x ) ( x − E ( X ) ) 2
= 1 / ( b − a + 1 ) ) ( ∑ x = a b ( x − b + a 2 ) 2 )
= ( b − a ) 2 12
توزیع گسسته یکنواخت در بسیاری از تقریب ها و مشاهدات ظاهر می شوند. مشاهده این توزیع ( به طور شهودی ) نشان دهنده نبود تفاوت مؤثر بین پیشامدها است. با استفاده از اصل حداکثر انتروپی می توان اثبات کرد وقتی چیزی جز مقادیر قابل مشاهده ( فضای نمونه ) نمی دانیم، باید احتمال تمام آن ها را برابر در نظر بگیریم. [ ۱]
اما مثال هایی وجود دارد که علی رغم نبود تفاوت میان حالات ( حداقل در نگاه اول ) ، توزیع رخدادها از توزیع یکنواخت بسیار متفاوت است. به طور مثال می توان یه قانون بنفورد اشاره کرد.
یک سیستم که خروجی هایش به طور مطلق از توزیع یکنواخت گسسته پیروی می کند کاریرد های فراوانی در نمونه برداری آماری، رمزنگاری، قمار و . . . دارد اما ساختن چنین ماشینی کار بسیار سختی است. امروزه از روش هایی مثل الگوریتم های کامپیوتری و دریافت تابش کیهانی برای تولید این خروجی ها استفاده می شود.


wiki: توزیع یکنواخت گسسته
