تَبَرزین به
تبرهای جنگی گفته می شود که مورد استفاده ایرانیان بوده و دارای دو تیغه برنده بوده تیغه اول برگ شکل بوده و مخصوص بریدن تیغه دوم مثل کلنگ بوده و مخصوص شکافت زره و کلاه خود ارتش دشمن بوده[ ۱]
تبرزین از ابزارهای جنگی در دوره
هخامنشیان بود و در روزگار ساسانیان، از جنگ افزار ارتش و واحدهای چریکی ارتش ساسانی و هخامنشی بوده که برای تکه تکه کردن ارتش دشمنان به کار می رفته در دوره های بعد تبرزین تنها کارایی نظامی نداشته بلکه یک نماد مخصوص
دراویش بود که چهره ایی عارفانه به وجود آورده است. [ ۲]
تبرزین (اروپایی). تبرزین اروپایی گونه ای از ابزارهای جنگی با دستهٔ بلند است که در قرون وسطی،
پیاده نظام و
شوالیه ها به فراوانی از آن استفاده می کرد.
ابزارهایی مانند تبرزین ( ایرانی ) ، ناچخ، تبر دانمارکی و باردیش ( تبرزین بلند ) هم وجود دارند که معمولاً با این نوع تبرزین اشتباه گرفته می شوند.
کاربرد تبرزین در اروپا به سدهٔ ۱۴ و ۱۵ میلادی بازمی گردد این تبرزین ها دستهٔ چوبی به درازای ۱٫۲ تا ۲ متر داشتند و یک سر فولادی داشتند البته در برخی موارد درازای دسته به ۲٫۴ متر نیز می رسید. طراحی بخش فولادی نیز در گذر زمان تغییر می کرد گاهی سری به شکل تبر و گاهی به شکل
چکش داشت.
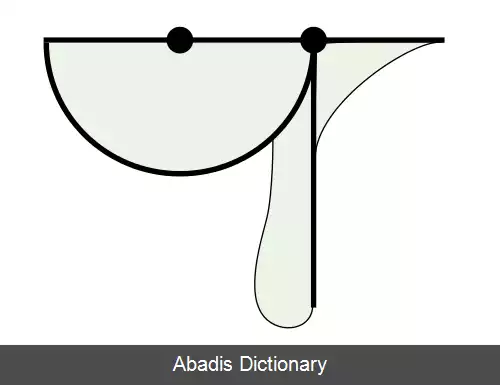
تبرزین (هندسه). تبرزین ( به انگلیسی: tomahawk ) ابزاری در
هندسه است که از آن برای تقسیم کردن یک زاویه به سه قسمت مساوی (
تثلیث زاویه ) استفاده می کنند. شکل ظاهری آن، شامل یک
نیم دایره و دو
پاره خط است که به صورتی قرار دارند که شکل یک تبرزین را تداعی می کند که یک نوع
تبر آمریکایی است. ابزاری مشابه نیز وجد داشته که به آن چاقوی کفاش گفته می شده، ولی امروزه این نام بیشتر به شکل هندسی دیگری به نام Arbelos اطلاق می شود. ( یک مثلث با اضلاع منحنی که توسط سه نیم دایرهٔ مماس برهم، تشکیل می شود )
شکل اصلی تبرزین، شامل این اجزاء می شود: یک نیم دایره ( تیغهٔ تبر ) ، یک پاره خط به اندازهٔ شعاع نیم دایره که در راستای
قطر آن ادامه داده شده است ( نوک یا سوزن تبر ) و یک پاره خط به اندازهٔ دلخواه ( به عنوان دستهٔ تبر ) عمود بر قطر نیم دایره. برای ساختن این ابزار به صورت فیزیکی، ممکن است دسته و نوک ( سوزن ) آن، ضخیم تر در نظر گرفته شود، به اندازه ای که پاره خط موازی با دستهٔ تبر، همچنان بخشی از محدودهٔ شکل هندسی باشد. برخلاف روش تثلیث زاویه با گونیا، طرف دیگر دسته ( که ضخیم تر می شود ) لازم نیست که موازی با پاره خط آن ساخته شود.
در برخی منابع به جای نیم دایره از دایرهٔ کامل استفاده می شود، یا تبرزین از قسمت نیم دایره هم موازی با قطر آن نیز ضخیم می شود، اما این تغییرات تفاوتی در عملکرد تبرزین به عنوان یک ابزار تثلیث زاویه ایجاد نمی کند.
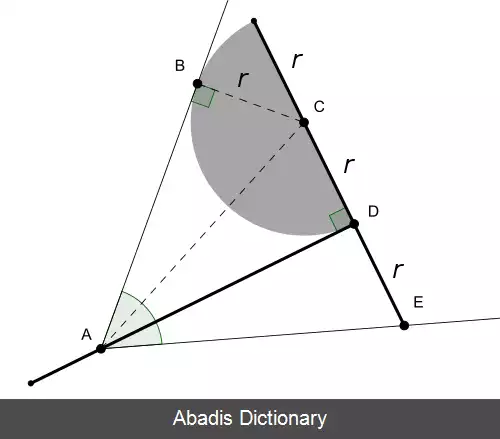
برای تثلیث زاویه با تبرزین، آن را به صورتی قرار می دهیم که دستهٔ آن از رأس زاویه بگذرد، همین طور یکی از اضلاع زاویه باید با نیم دایرهٔ تبرزین مماس شود و همچنین سوزن آن با ضلع دیگر زاویه برخورد کند. یکی از خطوطی که زاویه را به سه قسمت مساوی تقسیم می کند، پاره خط دستهٔ تبر است و خط دیگر، از مرکز نیم دایره می گذرد. اگر زاویه ای بسیار حاده ( تند ) باشد، با توجه به طول دستهٔ تبرزین، ممکن است نتوان تبرزین را داخل زاویه قرار داد. اما این مشکل را می توان با این راهکار برطرف کرد؛ زاویه را ( اضلاع آن را ) تا زمانی که تبرزین داخل آن قرار بگیرد، دو برابر می کنیم، حال پس از انجام تثلیث زاویه، آن را نصف کنیم تا ( اضلاع آن ) به اندازهٔ اولیه بازگردد.
اگر رأس زاویه را A، نقطهٔ مماس نیم دایره را B، مرکز نیم دایره را C، ابتدای دستهٔ تبر را D، و سوزن تبر را E بنامیم، آنگاه مثلث های ACD و ADE هر دو مثلث های قائم الزاویه ای هستند که دارای قاعده و ارتفاع یکسان هستند، پس با یکدیگر متشابه هستند. به علت این که ضلع های AB و BC هرکدام به ترتیب مماس بر نیم دایره و شعاع نیم دایره در نظر گرفته شده اند، بنابراین تشکیل زاویهٔ قائمه می دهند، بنابراین مثلث ABC نیز قائم الزاویه است. همچنین این مثلث، وتری مشترک با مثلث ACD دارد و همچنین BC = CD، بنابراین این مثلث نیز با دو مثلث دیگر متشابه است که بیانگر این است که سه زاویه ای که در رأس زاویهٔ اصلی ایجاد شده است، با یکدیگر برابر هستند.