در ریاضیات، تبدیل هیلبرت، عملگری خطی است که بر تابعی همچون ( u ( t عمل کرده و [ ( H[u ( t را نتیجه می دهد. این تبدیل به افتخار دیوید هیلبرت تبدیل هیلبرت نامیده شد. هیلبرت برای اولین بار از این تبدیل برای حل حالت خاصی از مسئله ریمن−هیلبرت استفاده کرد. در پردازش سیگنال از تبدیل هیلبرت برای یافتن سیگنال تحلیلی یک سیگنال استفاده می شود.
توضیحات:
۱ تبدیل هیلبرت توابع sin و cos را می توان از دیدگاه توزیعی در نظر گرفت، در غیر اینصورت انتگرال مربوطه به صورت مشروط همگرا است. اما اگر حدود انتگرال به صورت تناوبی تعریف شوند مشکل به طور کامل حل می شود.
۲ در برخی از منابع تبدیل هیلبرت با اختلاف در یک علامت منفی تعریف شده است. در اینصورت ستون چپ در یک منفی ضرب می شود.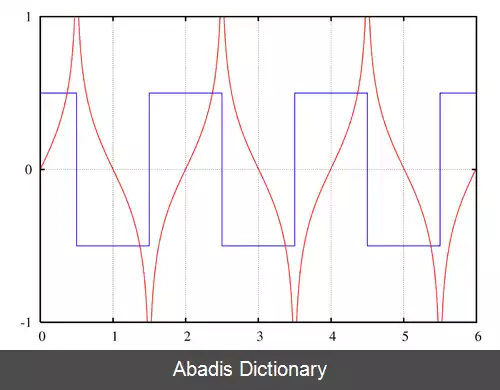
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتوضیحات:
۱ تبدیل هیلبرت توابع sin و cos را می توان از دیدگاه توزیعی در نظر گرفت، در غیر اینصورت انتگرال مربوطه به صورت مشروط همگرا است. اما اگر حدود انتگرال به صورت تناوبی تعریف شوند مشکل به طور کامل حل می شود.
۲ در برخی از منابع تبدیل هیلبرت با اختلاف در یک علامت منفی تعریف شده است. در اینصورت ستون چپ در یک منفی ضرب می شود.

wiki: تبدیل هیلبرت
