در ریاضیات، تنسور[ الف] ( Tensor ) شیئی جبری است که رابطه چندخطی بین مجموعه ها و اشیاء جبری مربوط به یک فضای برداری را توصیف می نماید. اشیائی که تنسورها آن ها را به یکدیگر می نگارند شامل اسکالرها، بردارها و حتی خود تنسورها می شوند. انواع زیادی از تنسورها شامل این موارد وجود دارند: اسکالرها، بردارها ( که جزو ساده ترین تنسورها می باشند ) ، بردارهای دوگان، نگاشت های چندخطی بین فضاهای برداری و حتی عملیاتی چون ضرب داخلی. تنسورها مستقل از هر پایه ای تعریف می شوند، گرچه که اغلب، مؤلفه های آن ها را برحسب پایهٔ مربوط به یک دستگاه مختصاتی به خصوصی نمایش می دهند.
تنسورها نقش مهمی را در فیزیک پیدا کرده اند، چرا که چهارچوب ریاضیاتی دقیقی را برای فرموله بندی و حل مسائل فیزیکی، در شاخه هایی چون این موارد را ارائه می نمایند: مکانیک ( تنش، کشسانی، مکانیک سیالات، گشتاور لختی، . . . ) ، الکترودینامیک ( تنسور الکترومغناطیسی، تنسور ماکسول، گذردهی، پذیرفتاری مغناطیسی، . . . ) ، نسبیت عام ( تنسور تنش - انرژی، تنسور انحنا، . . . ) و سایر زمینه ها. در مواردی از کاربردهای تنسور، ممکن است نیاز باشد که تنسور یک نقطه از یک شیء با تنسورهای تعریف شده از نقاط دیگر همان شیء متفاوت باشند، چنین مواردی ما را به سوی مفهوم میدان تنسوری می کشاند. در برخی از زمینه ها، میدان های تنسوری چنان رایج اند که از آن ها صرفاً به «تنسور» یاد می شود.
تولیو لوی - چیویتا و گرگریو ریچی - کورباسترو تنسورها را در ۱۹۰۰ میلادی ترویج دادند و بدین طریق کارهای قبلی برنهارت ریمان و الوین برونو کریستوفل و سایرین را به عنوان بخشی از حساب دیفرانسیل مطلق ادامه دادند. این مفهوم امکان فرموله بندی دیگری برای هندسه دیفرانسیل ذاتی یک منیفلد به فرم تنسور انحنای ریمانی را فراهم ساخت. [ ۱]
گرچه که تعاریف مختلف تنسورها به ظاهر متفاوت اند اما همه آن ها یک شیء هندسی را توصیف می نمایند، اما با زبان های متفاوت و در سطوح متفاوتی از تجرید. به عنوان مثال، تنسورها برای کاربردهای یادگیری ماشین نیز تعریف شده و مورد بحث قرار می گیرند. [ ۲]
تنسور را می توان به صورت آرایه ( معمولاً چندبعدی ) نمایش داد. درست همانگونه که یک بردار در یک فضای n - بعدی به صورت آرایه یک بعدی با n مؤلفه و نسبت به پایه دلخواهی نمایش داده می شود، هر تنسور را نیز می توان برحسب یک پایه و با کمک آرایه ای چندبعدی نمایش داد. به عنوان مثال، یک عملگر خطی را برحسب یک پایه و به صورت آرایه ای n × n نمایش داده می شود. درایه های این آرایه چندبعدی را مؤلفه های اسکالر تنسور نامیده یا صرفاً به آن ها مؤلفه ها می گویند. به کمک اندیس ها، موقعیت این درایه ها را در آرایه با کمک بالانویس ها و پایین نویس ها در کنار نماد تنسور مشخص می کنند. به عنوان مثال، مؤلفه های تنسور مرتبه ۲ را می توان به صورت T i j که در آن i و j اندیس هایی اند که مقادیرشان را از ۱ تا n انتخاب می کنند. همچنین ممکن است تنسور مرتبه دو به صورت T j i باشد. بالانویس یا پایین نویس بودن اندیس های تنسور بستگی به خواص تبدیل تنسور داشته که در ادامه توضیح داده خواهد شد. ازین رو در حالی که هردوی T j i و T i j را می توان به صورت ماتریس های n در n بیان نمود، هردوی آن ها از طریق عمل بالا و پایین پریدن اندیس ها ( index juggling ) به یکدیگر تبدیل نمود. از آنجا که خواص تبدیلی این دو نوع تنسور از یکدیگر متفاوت اند، نمی توان آن ها را به طریق مناسب با یکدیگر جمع نمود. تعداد کل اندیس های لازم جهت تعیین هر مؤلفه تنسور به طور یکتا، برابر بعد آرایه بوده و به آن مرتبه، درجه یا رتبه تنسور گویند. با این حال اصطلاح «رتبه» معنای دیگری در متون مربوط به ماتریس ها و تنسورها دارد.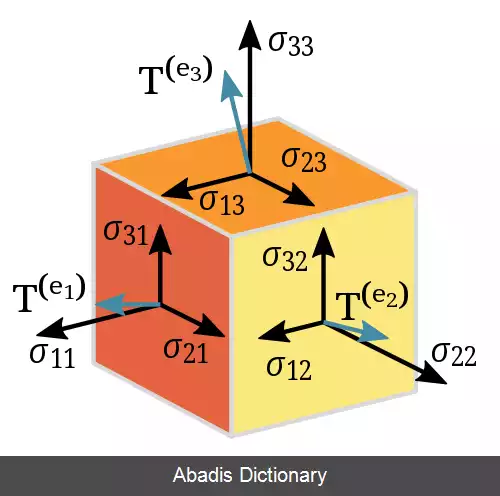
تنسورها نقش مهمی را در فیزیک پیدا کرده اند، چرا که چهارچوب ریاضیاتی دقیقی را برای فرموله بندی و حل مسائل فیزیکی، در شاخه هایی چون این موارد را ارائه می نمایند: مکانیک ( تنش، کشسانی، مکانیک سیالات، گشتاور لختی، . . . ) ، الکترودینامیک ( تنسور الکترومغناطیسی، تنسور ماکسول، گذردهی، پذیرفتاری مغناطیسی، . . . ) ، نسبیت عام ( تنسور تنش - انرژی، تنسور انحنا، . . . ) و سایر زمینه ها. در مواردی از کاربردهای تنسور، ممکن است نیاز باشد که تنسور یک نقطه از یک شیء با تنسورهای تعریف شده از نقاط دیگر همان شیء متفاوت باشند، چنین مواردی ما را به سوی مفهوم میدان تنسوری می کشاند. در برخی از زمینه ها، میدان های تنسوری چنان رایج اند که از آن ها صرفاً به «تنسور» یاد می شود.
تولیو لوی - چیویتا و گرگریو ریچی - کورباسترو تنسورها را در ۱۹۰۰ میلادی ترویج دادند و بدین طریق کارهای قبلی برنهارت ریمان و الوین برونو کریستوفل و سایرین را به عنوان بخشی از حساب دیفرانسیل مطلق ادامه دادند. این مفهوم امکان فرموله بندی دیگری برای هندسه دیفرانسیل ذاتی یک منیفلد به فرم تنسور انحنای ریمانی را فراهم ساخت. [ ۱]
گرچه که تعاریف مختلف تنسورها به ظاهر متفاوت اند اما همه آن ها یک شیء هندسی را توصیف می نمایند، اما با زبان های متفاوت و در سطوح متفاوتی از تجرید. به عنوان مثال، تنسورها برای کاربردهای یادگیری ماشین نیز تعریف شده و مورد بحث قرار می گیرند. [ ۲]
تنسور را می توان به صورت آرایه ( معمولاً چندبعدی ) نمایش داد. درست همانگونه که یک بردار در یک فضای n - بعدی به صورت آرایه یک بعدی با n مؤلفه و نسبت به پایه دلخواهی نمایش داده می شود، هر تنسور را نیز می توان برحسب یک پایه و با کمک آرایه ای چندبعدی نمایش داد. به عنوان مثال، یک عملگر خطی را برحسب یک پایه و به صورت آرایه ای n × n نمایش داده می شود. درایه های این آرایه چندبعدی را مؤلفه های اسکالر تنسور نامیده یا صرفاً به آن ها مؤلفه ها می گویند. به کمک اندیس ها، موقعیت این درایه ها را در آرایه با کمک بالانویس ها و پایین نویس ها در کنار نماد تنسور مشخص می کنند. به عنوان مثال، مؤلفه های تنسور مرتبه ۲ را می توان به صورت T i j که در آن i و j اندیس هایی اند که مقادیرشان را از ۱ تا n انتخاب می کنند. همچنین ممکن است تنسور مرتبه دو به صورت T j i باشد. بالانویس یا پایین نویس بودن اندیس های تنسور بستگی به خواص تبدیل تنسور داشته که در ادامه توضیح داده خواهد شد. ازین رو در حالی که هردوی T j i و T i j را می توان به صورت ماتریس های n در n بیان نمود، هردوی آن ها از طریق عمل بالا و پایین پریدن اندیس ها ( index juggling ) به یکدیگر تبدیل نمود. از آنجا که خواص تبدیلی این دو نوع تنسور از یکدیگر متفاوت اند، نمی توان آن ها را به طریق مناسب با یکدیگر جمع نمود. تعداد کل اندیس های لازم جهت تعیین هر مؤلفه تنسور به طور یکتا، برابر بعد آرایه بوده و به آن مرتبه، درجه یا رتبه تنسور گویند. با این حال اصطلاح «رتبه» معنای دیگری در متون مربوط به ماتریس ها و تنسورها دارد.

wiki: تانسور
تانسور (روستا). تنسور ( به انگلیسی: Tansor ) یک روستا و محله مدنی در بریتانیا است که در East Northamptonshire واقع شده است. [ ۱] تنسور ۱۷۲ نفر جمعیت دارد.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف

wiki: تانسور (روستا)
