در نظریه اعداد تابع فی اویلر یا تابعی است که تعداد اعداد طبیعی کوچکتر مساوی n که نسبت به n اول اند را می شمارد. اگر n یک عدد طبیعی مثبت باشد، آنگاه برابر است با تعداد اعداد طبیعی k در بازه ۱ تا n به طوری که بزرگترین مقسوم علیه مشترک ( ب. م. م ) n و k برابر ۱ باشد. تابع فی اویلر یک تابع ضربی است، بدین معنی که اگر دو عدد m و n نسبت به هم اول باشند آنگاه φ ( m n ) = φ ( m ) φ ( n ) . برای مثال ( 9 ) φ برابر ۶ است. زیرا اعداد ۱، ۲، ۴، ۵، ۷ و ۸ نسبت به ۹ اول هستند.
تابع فی اویلر نقش کلیدی در تعریف سیستم رمزنگاری RSA دارد.
لئونارد اولر این تابع را در سال ۱۷۶۳ معرفی کرد. در آن زمان او هنوز نماد خاصی برای این تابع تعیین نکرده بود. بعدها لئونارد اویلر با مطالعه بیشتر تابع فی، حرف یونانی π را برای آن برگزید. نماد استاندارد φ بعدها توسط گاوس استفاده شده است.
چندین راه برای محاسبه این فرمول وجود دارد.
این تابع بیان می کند که:
که در آن p یک عدد اول است به طوری که n بر p بخش پذیر نیست.
مقدار تابع فی برابر است با مقدار تبدیل فوریه گسسته ب. م. م در ۱ یعنی:
مقدار حقیقی این فرمول برابر است با:
توجه کنید که برخلاف دو فرمول دیگر در این فرمول نیازی به دانستن عوامل اول n نیست. اما چون فرمول شامل محاسبه ب. م. م n و همه اعداد مثبت کمتر از n است در نهایت به تجزیه n نیاز خواهیم داشت.
فرمول کلاسیک اویلر
این فرمول به روش های مختلف قابل اثبات است.
برای n> 1 می توان تابع فی را به عنوان یک حد تابع زتای ریمان محاسبه کرد
که در این فرمول
ζ ( s ) تابع زتای ریمان است، μ تابع موبیوس است، e عدد نپر است، و d مقسوم علیه است.
۹۹ مقدار اولیه این تابع در جدول و نمودار زیر قابل مشاهده است.
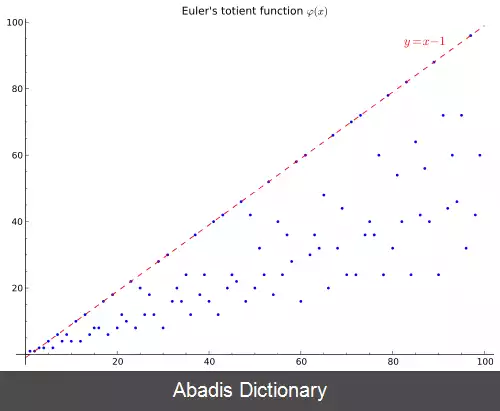
خط y = n - 1 یک کران بالا برای تابع است و زمانی رخ می دهد که n اول باشد.
بیان می کند: اگر n و a نسبت به هم اول باشند آنگاه
در حالت خاصی که n عدد اول باشد این قضیه به قضیه کوچک فرما معروف است. این قضیه از قضیه لاگرانژ نتیجه می شود.
سیستم رمزنگاری RSA بر روی همین قضیه بنا شده است: بیان می کنید که معکوس تابع a ↦ a d mod n در واقع همان تابع b ↦ b e mod n است که e معکوس ضربی d به پیمانه است.
• a ∣ b {\displaystyle a\mid b} → φ ( a ) ∣ φ ( b ) . {\displaystyle \varphi ( a ) \mid \varphi ( b ) . }
• n ∣ φ ( a n − 1 ) {\displaystyle n\mid \varphi ( a^{n} - 1 ) } ( a, n> 1 )
• φ ( m n ) = φ ( m ) φ ( n ) ⋅ d φ ( d ) {\displaystyle \varphi ( mn ) =\varphi ( m ) \varphi ( n ) \cdot {\frac {d}{\varphi ( d ) }}} d = gcd ( m, n ) .
• φ ( 2 m ) = { 2 φ ( m ) if m is even φ ( m ) if m is odd {\displaystyle \varphi ( 2m ) ={\begin{cases}2\varphi ( m ) & {\text{ if }}m{\text{ is even}}\\\varphi ( m ) & {\text{ if }}m{\text{ is odd}}\end{cases}}}
• φ ( n m ) = n m − 1 φ ( n ) . {\displaystyle \; \varphi \left ( n^{m}\right ) =n^{m - 1}\varphi ( n ) . }
• φ ( l c m ( m , n ) ) ⋅ φ ( g c d ( m , n ) ) = φ ( m ) ⋅ φ ( n ) . {\displaystyle \varphi ( \mathrm {lcm} ( m, n ) ) \cdot \varphi ( \mathrm {gcd} ( m, n ) ) =\varphi ( m ) \cdot \varphi ( n ) . }
• ∑ d ∣ n μ 2 ( d ) φ ( d ) = n φ ( n ) {\displaystyle \sum _{d\mid n}{\frac {\mu ^{2} ( d ) }{\varphi ( d ) }}={\frac {n}{\varphi ( n ) }}}
• ∑ 1 ≤ k ≤ n ( k , n ) = 1 k = 1 2 n φ ( n ) for n > 1 {\displaystyle \sum _{1\leq k\leq n \atop ( k, n ) =1}\!\!k={\frac {1}{2}}n\varphi ( n ) {\text{ for }}n> 1}
• ∑ k = 1 n φ ( k ) = 1 2 ( 1 + ∑ k = 1 n μ ( k ) ⌊ n k ⌋ 2 ) {\displaystyle \sum _{k=1}^{n}\varphi ( k ) ={\frac {1}{2}}\left ( 1+\sum _{k=1}^{n}\mu ( k ) \left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right ) }
• ∑ k = 1 n φ ( k ) k = ∑ k = 1 n μ ( k ) k ⌊ n k ⌋ = 6 π 2 n + O ( ( log n ) 2 / 3 ( log log n ) 4 / 3 ) {\displaystyle \sum _{k=1}^{n}{\frac {\varphi ( k ) }{k}}=\sum _{k=1}^{n}{\frac {\mu ( k ) }{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+{\mathcal {O}}\left ( ( \log n ) ^{2/3} ( \log \log n ) ^{4/3}\right ) }
• ∑ k = 1 n k φ ( k ) = 315 ζ ( 3 ) 2 π 4 n − log n 2 + O ( ( log n ) 2 / 3 ) {\displaystyle \sum _{k=1}^{n}{\frac {k}{\varphi ( k ) }}={\frac {315\zeta ( 3 ) }{2\pi ^{4}}}n - {\frac {\log n}{2}}+{\mathcal {O}}\left ( ( \log n ) ^{2/3}\right ) }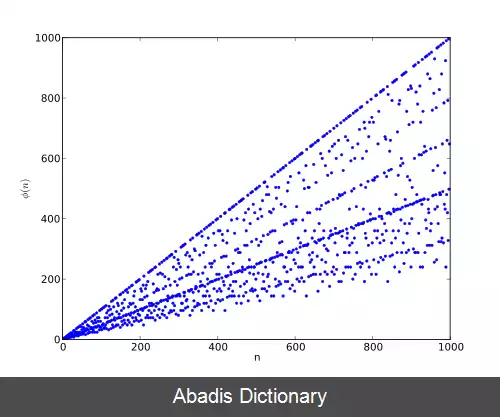
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع فی اویلر نقش کلیدی در تعریف سیستم رمزنگاری RSA دارد.
لئونارد اولر این تابع را در سال ۱۷۶۳ معرفی کرد. در آن زمان او هنوز نماد خاصی برای این تابع تعیین نکرده بود. بعدها لئونارد اویلر با مطالعه بیشتر تابع فی، حرف یونانی π را برای آن برگزید. نماد استاندارد φ بعدها توسط گاوس استفاده شده است.
چندین راه برای محاسبه این فرمول وجود دارد.
این تابع بیان می کند که:
که در آن p یک عدد اول است به طوری که n بر p بخش پذیر نیست.
مقدار تابع فی برابر است با مقدار تبدیل فوریه گسسته ب. م. م در ۱ یعنی:
مقدار حقیقی این فرمول برابر است با:
توجه کنید که برخلاف دو فرمول دیگر در این فرمول نیازی به دانستن عوامل اول n نیست. اما چون فرمول شامل محاسبه ب. م. م n و همه اعداد مثبت کمتر از n است در نهایت به تجزیه n نیاز خواهیم داشت.
فرمول کلاسیک اویلر
این فرمول به روش های مختلف قابل اثبات است.
برای n> 1 می توان تابع فی را به عنوان یک حد تابع زتای ریمان محاسبه کرد
که در این فرمول
ζ ( s ) تابع زتای ریمان است، μ تابع موبیوس است، e عدد نپر است، و d مقسوم علیه است.
۹۹ مقدار اولیه این تابع در جدول و نمودار زیر قابل مشاهده است.
خط y = n - 1 یک کران بالا برای تابع است و زمانی رخ می دهد که n اول باشد.
بیان می کند: اگر n و a نسبت به هم اول باشند آنگاه
در حالت خاصی که n عدد اول باشد این قضیه به قضیه کوچک فرما معروف است. این قضیه از قضیه لاگرانژ نتیجه می شود.
سیستم رمزنگاری RSA بر روی همین قضیه بنا شده است: بیان می کنید که معکوس تابع a ↦ a d mod n در واقع همان تابع b ↦ b e mod n است که e معکوس ضربی d به پیمانه است.
• a ∣ b {\displaystyle a\mid b} → φ ( a ) ∣ φ ( b ) . {\displaystyle \varphi ( a ) \mid \varphi ( b ) . }
• n ∣ φ ( a n − 1 ) {\displaystyle n\mid \varphi ( a^{n} - 1 ) } ( a, n> 1 )
• φ ( m n ) = φ ( m ) φ ( n ) ⋅ d φ ( d ) {\displaystyle \varphi ( mn ) =\varphi ( m ) \varphi ( n ) \cdot {\frac {d}{\varphi ( d ) }}} d = gcd ( m, n ) .
• φ ( 2 m ) = { 2 φ ( m ) if m is even φ ( m ) if m is odd {\displaystyle \varphi ( 2m ) ={\begin{cases}2\varphi ( m ) & {\text{ if }}m{\text{ is even}}\\\varphi ( m ) & {\text{ if }}m{\text{ is odd}}\end{cases}}}
• φ ( n m ) = n m − 1 φ ( n ) . {\displaystyle \; \varphi \left ( n^{m}\right ) =n^{m - 1}\varphi ( n ) . }
• φ ( l c m ( m , n ) ) ⋅ φ ( g c d ( m , n ) ) = φ ( m ) ⋅ φ ( n ) . {\displaystyle \varphi ( \mathrm {lcm} ( m, n ) ) \cdot \varphi ( \mathrm {gcd} ( m, n ) ) =\varphi ( m ) \cdot \varphi ( n ) . }
• ∑ d ∣ n μ 2 ( d ) φ ( d ) = n φ ( n ) {\displaystyle \sum _{d\mid n}{\frac {\mu ^{2} ( d ) }{\varphi ( d ) }}={\frac {n}{\varphi ( n ) }}}
• ∑ 1 ≤ k ≤ n ( k , n ) = 1 k = 1 2 n φ ( n ) for n > 1 {\displaystyle \sum _{1\leq k\leq n \atop ( k, n ) =1}\!\!k={\frac {1}{2}}n\varphi ( n ) {\text{ for }}n> 1}
• ∑ k = 1 n φ ( k ) = 1 2 ( 1 + ∑ k = 1 n μ ( k ) ⌊ n k ⌋ 2 ) {\displaystyle \sum _{k=1}^{n}\varphi ( k ) ={\frac {1}{2}}\left ( 1+\sum _{k=1}^{n}\mu ( k ) \left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right ) }
• ∑ k = 1 n φ ( k ) k = ∑ k = 1 n μ ( k ) k ⌊ n k ⌋ = 6 π 2 n + O ( ( log n ) 2 / 3 ( log log n ) 4 / 3 ) {\displaystyle \sum _{k=1}^{n}{\frac {\varphi ( k ) }{k}}=\sum _{k=1}^{n}{\frac {\mu ( k ) }{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+{\mathcal {O}}\left ( ( \log n ) ^{2/3} ( \log \log n ) ^{4/3}\right ) }
• ∑ k = 1 n k φ ( k ) = 315 ζ ( 3 ) 2 π 4 n − log n 2 + O ( ( log n ) 2 / 3 ) {\displaystyle \sum _{k=1}^{n}{\frac {k}{\varphi ( k ) }}={\frac {315\zeta ( 3 ) }{2\pi ^{4}}}n - {\frac {\log n}{2}}+{\mathcal {O}}\left ( ( \log n ) ^{2/3}\right ) }


wiki: تابع فی اویلر
