توابع بسل اولین بار توسط دانیل برنولی تعریف شد و سپس فردریش بسل فرم عمومی آن را بررسی نمود. توابع بسل جواب هایِ معادله دیفرانسیل زیر می باشند[ ۱] :
x 2 d 2 y d x 2 + x d y d x + ( m 2 x 2 − α 2 ) y = 0
معادلهٔ بسلی معادله ای است که از معادلات قابل حل با سری هاست و دارای نقطه تکین منظّم است. نقطهٔ x = 0 یگانه نقطهٔ غیرعادی معادلهٔ فوق است. جواب های متعامد معادله اشتورم - لیوویل به توابع بسل معروفند.
تابعِ بسل اصلاح شده:
x 2 d 2 y dx 2 + x dy dx − ( x 2 + n 2 ) y = 0
در معادلهٔ بالا، n یک عدد صحیح است که مرتبهٔ تابع بسل را مشخص می کند. به طورکلّی، توابع بسل از حل معادلات دیفرانسیل پاره ای لاپلاس و معادله هلمهولتز در مختصات استوانه ای و مختصات کروی بدست می آید. از این رو، این توابع در تئوری انتشار امواج و تئوری پتانسیل اهمیت به سزایی دارد، البته این توابع در حل معادلات ارتعاشات، معادلات رسانایی گرما و امواج الکترومغناطیس در مختصات استوانه ای ظاهر می شود.
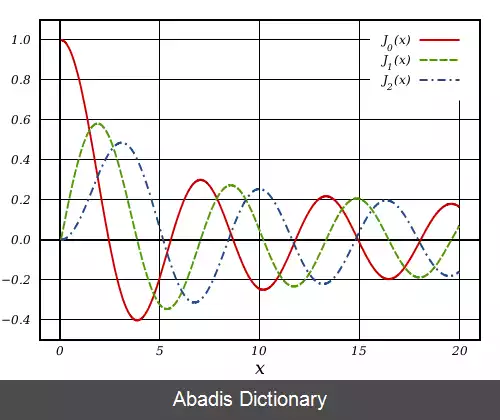
تابع بسل نوع اول آن دستهٔ از توابعی هستند که مربوط به α بوده و به عنوان عدد طبیعی منفی هستند که در صفر متناهی می باشد:
که Γ ( z ) تابع گاما است که حالت کلّی فاکتوریل برای اعداد غیرطبیعی است.
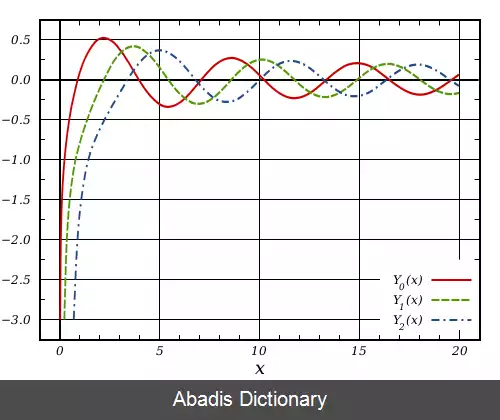
توابع بسل نوع دوم آن دسته توابعی هستند که در مبدأ مختصات ( نقطه صفر ) تکینه هستند:
Y α ( x ) = J α ( x ) cos ( α π ) − J − α ( x ) sin ( α π )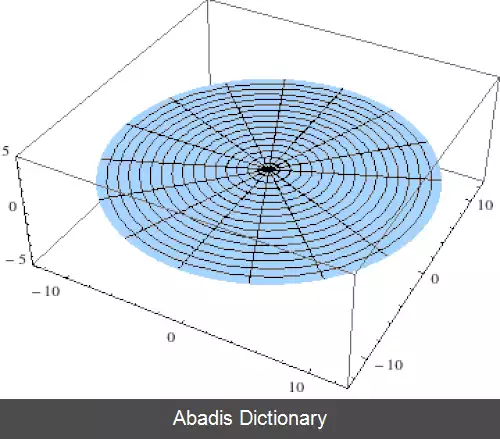
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفx 2 d 2 y d x 2 + x d y d x + ( m 2 x 2 − α 2 ) y = 0
معادلهٔ بسلی معادله ای است که از معادلات قابل حل با سری هاست و دارای نقطه تکین منظّم است. نقطهٔ x = 0 یگانه نقطهٔ غیرعادی معادلهٔ فوق است. جواب های متعامد معادله اشتورم - لیوویل به توابع بسل معروفند.
تابعِ بسل اصلاح شده:
x 2 d 2 y dx 2 + x dy dx − ( x 2 + n 2 ) y = 0
در معادلهٔ بالا، n یک عدد صحیح است که مرتبهٔ تابع بسل را مشخص می کند. به طورکلّی، توابع بسل از حل معادلات دیفرانسیل پاره ای لاپلاس و معادله هلمهولتز در مختصات استوانه ای و مختصات کروی بدست می آید. از این رو، این توابع در تئوری انتشار امواج و تئوری پتانسیل اهمیت به سزایی دارد، البته این توابع در حل معادلات ارتعاشات، معادلات رسانایی گرما و امواج الکترومغناطیس در مختصات استوانه ای ظاهر می شود.
تابع بسل نوع اول آن دستهٔ از توابعی هستند که مربوط به α بوده و به عنوان عدد طبیعی منفی هستند که در صفر متناهی می باشد:
که Γ ( z ) تابع گاما است که حالت کلّی فاکتوریل برای اعداد غیرطبیعی است.
توابع بسل نوع دوم آن دسته توابعی هستند که در مبدأ مختصات ( نقطه صفر ) تکینه هستند:
Y α ( x ) = J α ( x ) cos ( α π ) − J − α ( x ) sin ( α π )



wiki: تابع بسل
