در ریاضیات، به طور ویژه در نظریه اعداد، تابع اعداد اول، تابعی از اعداد طبیعی به اعداد طبیعی همانند تابع فاکتوریل می باشد که به جای ضرب اعداد صحیح مثبت، اعداد اول صرفاً ضرب می شوند. دو تعریف متضاد وجود دارد که تفسیر این استدلال را متفاوت می کند: تعبیر استدلال اول بیان می دارد که در دنباله اعداد اول شاخص وجود دارد ( پس این تابع اکیداً صعودی است ) درحالیکه تعبیر استدلال دوم بیان می دارد که اعداد اول برای ضرب، معین اند ( پس مقدار تابع در هر عدد مرکب، مشابه مقدار قبلی خود می باشد ) این مقاله از تعبیر دوم استفاده می کند. عبارت «تابع اعداد اول»، منسوب به Harvey Dubner، با اعداد اول متناسب است همان طور که تابع عوامل ( فاکتوریل ) با عوامل رابطه دارد.
تابع اعداد اول، pn، برای nامین عدد اول، عبارت #pn حاصل nتا عدد اول تعریف می شود. [ ۱] [ ۲]
که pk، kامین عدد اول می باشد. به عنوان مثال، p5# دلالت بر حاصل ۵ عدد اول دارد:
برای ۶ تابع اعداد اول، pn# به صورت زیر است:
این دنباله شامل p0# = ۱ نیز به عنوان حاصل پوچ ( هسته یا همان کرنل ) می باشد. تابع اعداد اول pn# مطابق زیر رشد می کند:
که o ( ⋅ ) نماد oکوچک می باشد. [ ۲]
در کل، برای هر عدد صحیح مثبت n همانند تابع اعداد اول، #n به صورت حاصل اعداد اول که ≤ n:[ ۱] [ ۳] هستند، تعریف می شود.
که π ( n ) ''تابع شمارش اعداد اول''است؛ که تعداد اعداد اول ≤ n را می دهد؛ و معادل زیر است:
برای مثال ۱۲# حاصل اعداد اول ≤ ۱۲ را بیان می دارد.
زیرا π ( 12 ) = 5 را می توان از طریق زیر محاسبه کرد:
مقادیر تابع اعداد اول را برای ۱۲ مقدار اول n\# در نظر بگیرید. ۱، ۲، ۶، ۶، ۳۰، ۳۰، ۲۱۰، ۲۱۰، ۲۱۰، ۲۱۰، ۲۳۱۰، ۲۳۱۰. می بینیم که برای هر عدد مرکب n هر جملهٔ n# جملهٔ ماقبل خود را تکثیر می کند ( n − ۱ ) # چنانچه در تعریف گفته شد. در مثال بالا داریم 12# = p5# = ۱۱# زیرا ۱۲ عددی مرکب است.
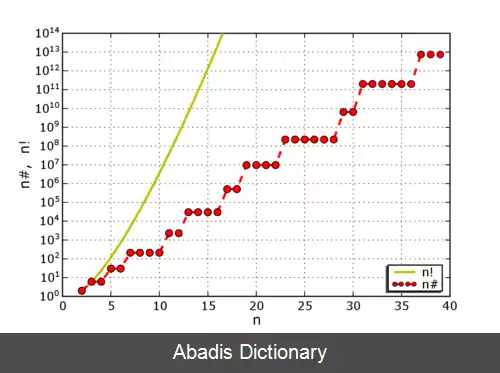
لگاریتم طبیعی n# اولین تابع چبیشف است که به صورت θ ( n ) یا ϑ ( n ) نوشته می شود که برای nهای بزرگ به n نزدیک می شود. . [ ۴] نظر ضرب کردن همه اعداد اول شناخته شده در اثبات نامحدود بودن اعداد اول، به وقوع پیوست؛ که از آن برای وجود اشتقاقی سایر اعداد اول استفاده می شود.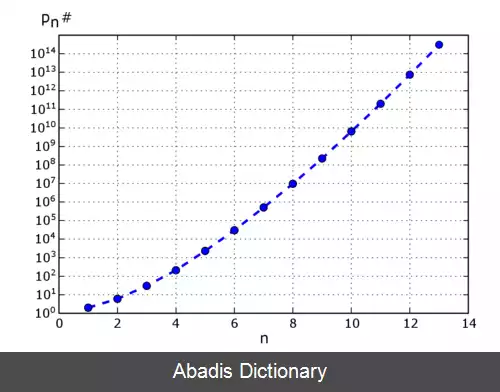
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع اعداد اول، pn، برای nامین عدد اول، عبارت #pn حاصل nتا عدد اول تعریف می شود. [ ۱] [ ۲]
که pk، kامین عدد اول می باشد. به عنوان مثال، p5# دلالت بر حاصل ۵ عدد اول دارد:
برای ۶ تابع اعداد اول، pn# به صورت زیر است:
این دنباله شامل p0# = ۱ نیز به عنوان حاصل پوچ ( هسته یا همان کرنل ) می باشد. تابع اعداد اول pn# مطابق زیر رشد می کند:
که o ( ⋅ ) نماد oکوچک می باشد. [ ۲]
در کل، برای هر عدد صحیح مثبت n همانند تابع اعداد اول، #n به صورت حاصل اعداد اول که ≤ n:[ ۱] [ ۳] هستند، تعریف می شود.
که π ( n ) ''تابع شمارش اعداد اول''است؛ که تعداد اعداد اول ≤ n را می دهد؛ و معادل زیر است:
برای مثال ۱۲# حاصل اعداد اول ≤ ۱۲ را بیان می دارد.
زیرا π ( 12 ) = 5 را می توان از طریق زیر محاسبه کرد:
مقادیر تابع اعداد اول را برای ۱۲ مقدار اول n\# در نظر بگیرید. ۱، ۲، ۶، ۶، ۳۰، ۳۰، ۲۱۰، ۲۱۰، ۲۱۰، ۲۱۰، ۲۳۱۰، ۲۳۱۰. می بینیم که برای هر عدد مرکب n هر جملهٔ n# جملهٔ ماقبل خود را تکثیر می کند ( n − ۱ ) # چنانچه در تعریف گفته شد. در مثال بالا داریم 12# = p5# = ۱۱# زیرا ۱۲ عددی مرکب است.
لگاریتم طبیعی n# اولین تابع چبیشف است که به صورت θ ( n ) یا ϑ ( n ) نوشته می شود که برای nهای بزرگ به n نزدیک می شود. . [ ۴] نظر ضرب کردن همه اعداد اول شناخته شده در اثبات نامحدود بودن اعداد اول، به وقوع پیوست؛ که از آن برای وجود اشتقاقی سایر اعداد اول استفاده می شود.


wiki: تابع اعداد اول
