بزرگترین مقسوم علیه مشترک ( اختصاری {{{1}}} ) ( به انگلیسی: Greatest common divisor ( GCD ) ) در ریاضیات بزرگترین عضو مجموعهٔ شمارنده های دو عدد بزرگترین مقسوم علیه مشترک این دو عدد نامیده می شود.
فرض کنید a و b دو عدد صحیح دلخواه اند. اگر D ( a ) و D ( b ) به ترتیب مجموعهٔ مقسوم علیه های مثبت a و b باشند، آن گاه بزرگترین مقسوم علیه مشترک و که با نماد ( a , b ) نمایش داده می شود و به شکل زیر تعریف می شود. بزرگترین عضو مجموعهٔ مقسوم علیه های مشترک و مثبت a و ( a , b ) = b .
• اگر ( a , b ) = 1 {\displaystyle ( a, b ) =1} ، آن گاه a {\displaystyle a} و b {\displaystyle b} را نسبت به هم اول یا متباین می خوانیم.
• ( a , b ) = ( − a , b ) = ( a , − b ) = ( − a , − b ) {\displaystyle ( a, b ) = ( - a, b ) = ( a, - b ) = ( - a, - b ) }
• ( 0 , a ) = | a | {\displaystyle ( 0, a ) =|a|}
• چون D ( 0 ) = 1 , 2 , 3 , . . . {\displaystyle D ( 0 ) ={1, 2, 3, . . . }} ، پس مجموعهٔ مقسوم علیه های صفر و صفر مجموعهٔ اعداد طبیعی است که بزرگترین عضو ندارد، پس ( 0 , 0 ) {\displaystyle ( 0, 0 ) } تعریف نشده است. تذکر: برخی از مؤلفین تعریف می کنند ( 0 , 0 ) = 0 {\displaystyle ( 0, 0 ) =0} .
• به ازای هر عدد صحیح k {\displaystyle k} داریم: ( a , b ) = ( a , k a + b ) {\displaystyle ( a, b ) = ( a, ka+b ) } .
• قضیه بزو ( Bezout ) : فرض کنید a {\displaystyle a} و b {\displaystyle b} دو عدد صحیحی هستند که حداقل یکی از آن ها مخالف صفر است. اگر ( a , b ) = d {\displaystyle ( a, b ) =d} ، در این صورت، اعداد صحیح r {\displaystyle r} و s {\displaystyle s} وجود دارند به طوری که
d = r a + s b
در این روش با نوشتن مجموعهٔ مقسوم علیه های دو عدد مورد نظر و اشتراک این دو مجموعه، بزرگترین مقسوم علیه مشترک را پیدا می کنیم.
در این روش، ابتدا دو عدد مزبور را به عوامل اول تجزیه کرده، سپس سازه های ( عدد های ) مشترک با توان کمتر را در هم ضرب می کنیم، ب. م. م بدست می آید.
در این روش، ابتدا عدد بزرگتر را بر دیگری تقسیم می کنیم و سپس عدد کوچکتر را بر باقی ماندهٔ تقسیم مزبور تقسیم می کنیم و این عمل را تا جایی که باقی مانده صفر شود ادامه می دهیم، آخرین باقی مانده غیرصفر، بزرگترین مقسوم علیه مشترک دو عدد مزبور است.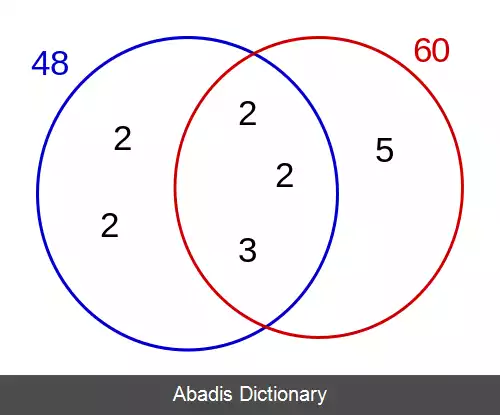
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید a و b دو عدد صحیح دلخواه اند. اگر D ( a ) و D ( b ) به ترتیب مجموعهٔ مقسوم علیه های مثبت a و b باشند، آن گاه بزرگترین مقسوم علیه مشترک و که با نماد ( a , b ) نمایش داده می شود و به شکل زیر تعریف می شود. بزرگترین عضو مجموعهٔ مقسوم علیه های مشترک و مثبت a و ( a , b ) = b .
• اگر ( a , b ) = 1 {\displaystyle ( a, b ) =1} ، آن گاه a {\displaystyle a} و b {\displaystyle b} را نسبت به هم اول یا متباین می خوانیم.
• ( a , b ) = ( − a , b ) = ( a , − b ) = ( − a , − b ) {\displaystyle ( a, b ) = ( - a, b ) = ( a, - b ) = ( - a, - b ) }
• ( 0 , a ) = | a | {\displaystyle ( 0, a ) =|a|}
• چون D ( 0 ) = 1 , 2 , 3 , . . . {\displaystyle D ( 0 ) ={1, 2, 3, . . . }} ، پس مجموعهٔ مقسوم علیه های صفر و صفر مجموعهٔ اعداد طبیعی است که بزرگترین عضو ندارد، پس ( 0 , 0 ) {\displaystyle ( 0, 0 ) } تعریف نشده است. تذکر: برخی از مؤلفین تعریف می کنند ( 0 , 0 ) = 0 {\displaystyle ( 0, 0 ) =0} .
• به ازای هر عدد صحیح k {\displaystyle k} داریم: ( a , b ) = ( a , k a + b ) {\displaystyle ( a, b ) = ( a, ka+b ) } .
• قضیه بزو ( Bezout ) : فرض کنید a {\displaystyle a} و b {\displaystyle b} دو عدد صحیحی هستند که حداقل یکی از آن ها مخالف صفر است. اگر ( a , b ) = d {\displaystyle ( a, b ) =d} ، در این صورت، اعداد صحیح r {\displaystyle r} و s {\displaystyle s} وجود دارند به طوری که
d = r a + s b
در این روش با نوشتن مجموعهٔ مقسوم علیه های دو عدد مورد نظر و اشتراک این دو مجموعه، بزرگترین مقسوم علیه مشترک را پیدا می کنیم.
در این روش، ابتدا دو عدد مزبور را به عوامل اول تجزیه کرده، سپس سازه های ( عدد های ) مشترک با توان کمتر را در هم ضرب می کنیم، ب. م. م بدست می آید.
در این روش، ابتدا عدد بزرگتر را بر دیگری تقسیم می کنیم و سپس عدد کوچکتر را بر باقی ماندهٔ تقسیم مزبور تقسیم می کنیم و این عمل را تا جایی که باقی مانده صفر شود ادامه می دهیم، آخرین باقی مانده غیرصفر، بزرگترین مقسوم علیه مشترک دو عدد مزبور است.

