برآورد چگالی. در آمار و احتمال، برآورد چگالی ( به انگلیسی: Density estimation ) به فرایند تخمین تابع چگالی احتمال یک متغیر تصادفی با استفاده از نمونه های مشاهده شده از آن متغیر گفته می شود. معمولاً فرض می شود نمونه های مشاهده شده به طور تصادفی و مستقل براساس تابع توزیع احتمال، توزیع شده اند.
برای حل مسئله برآورد چگالی، روش های مختلفی استفاده شده است، از جمله پنجره پارزن ( به انگلیسی: Parzen Window ) و تعدادی روش های مبتنی بر دسته بندی داده، از جمله کوانتیزاسیون برداری. ساده ترین روش برای برآورد چگالی، استفاده از یک بافت نگاشت تغییر مقیاس یافته است.
در این مثال نمونه های مربوط به بیماری دیابت را بررسی می کنیم. در زیر توضیحات مربوط به مجموعه داده آورده شده است:
جمعیتی از زنان بالای ۲۰ سال از پیما که در Phoenix, Arizona زندگی می کردند، با شاخص سازمان جهانی بهداشت مورد ارزیابی دیابت شیرین قرار گرفتند. داده ها توسط مؤسسه ملی بیماری های دیابتی و گوارشی و کلیوی آمریکا ( US National Institute of Diabetes and Digestive and Kidney Diseases ) جمع آوری شده است. ما از ۵۳۲ نمونه استفاده کردیم. [ ۲] [ ۳]
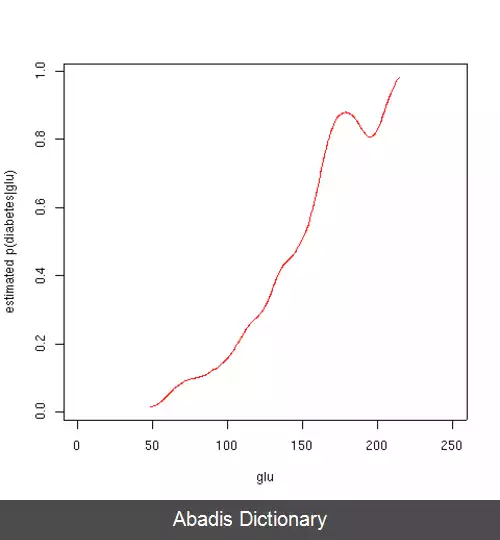
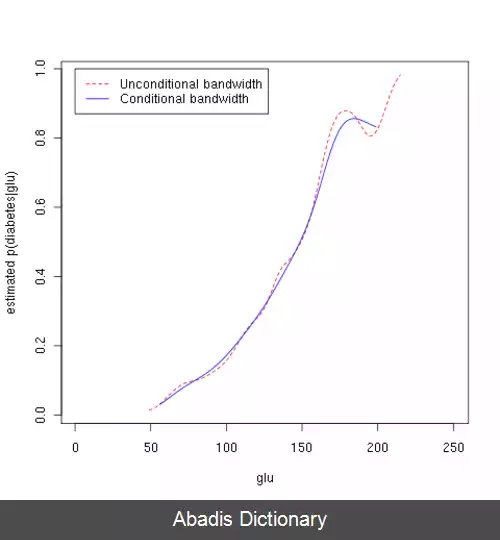
در این مثال، ما ۳ برآورد چگالی برای "glu" ( با تمرکز بر روی گلوکز پلاسما ( به انگلیسی: plasma glucose ) ) انجام دادیم. یکی از آنها احتمال شرطی به شرط مبتلا بودن به دیابت، دومی به شرط مبتلا نبودن به دیابت و سومی بدون شرطی روی داشتن یا نداشتن دیابت است. سپس از برآوردهایی که برای احتمالات شرطی به دست آمد استفاده شد تا احتمال ابتلا به دیابت به شرط "glu" بدست بیاید.
داده های مربوط به "glu" از پکیچ MASS[ ۴] موجود در زبان برنامه نویسی آر بدست آمد. داده ها به طور کامل تر از طریق Pima. tr? و Pima. te? در زبان آر، قابل دسترسی است.
میانگین و انحراف معیار "glu" در کیس های مبتلا به دیابت به ترتیب برابر ۱۴۳٫۱ و ۳۱٫۲۶ است. در کیس های بدون دیابت، این مقادیر به ترتیب برابر ۱۱۰٫۰ و ۲۴٫۲۹ است. با توجه به این مقادیر، می توان دریافت که نمونه های مبتلا به دیابت دارای مقادیر بالاتری از "glu" هستند. این نکته با بررسی نمودارهای برآورد شده از توابع چگالی قابل فهم تر است.
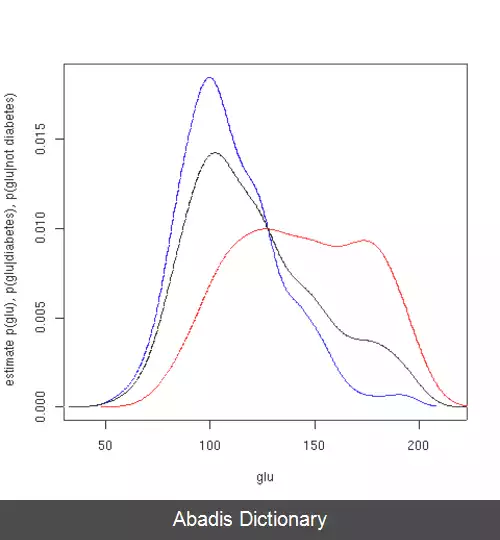
شکل اول برآورد چگالی از احتمالات p ( glu | diabetes=۱ ) و p ( glu | diabetes=۰ ) و p ( glu ) را نشان می دهد. چگالی های برآورد شده، برآوردهای چگالی هسته هستند که با استفاده از هستهٔ گاوسی به دست آمده اند. به بیان دیگر، یک تابع چگالی گاوسی بر روی هر نقطه از داده قرار داده شده است، به طوری که مرکز تابع چگالی نقطه مدنظر باشد، سپس مجموع توابع چگالی روی گستره داده ها محاسبه شده است.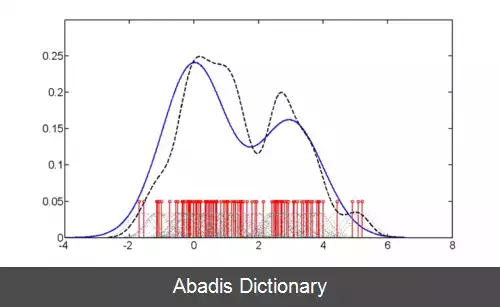
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای حل مسئله برآورد چگالی، روش های مختلفی استفاده شده است، از جمله پنجره پارزن ( به انگلیسی: Parzen Window ) و تعدادی روش های مبتنی بر دسته بندی داده، از جمله کوانتیزاسیون برداری. ساده ترین روش برای برآورد چگالی، استفاده از یک بافت نگاشت تغییر مقیاس یافته است.
در این مثال نمونه های مربوط به بیماری دیابت را بررسی می کنیم. در زیر توضیحات مربوط به مجموعه داده آورده شده است:
جمعیتی از زنان بالای ۲۰ سال از پیما که در Phoenix, Arizona زندگی می کردند، با شاخص سازمان جهانی بهداشت مورد ارزیابی دیابت شیرین قرار گرفتند. داده ها توسط مؤسسه ملی بیماری های دیابتی و گوارشی و کلیوی آمریکا ( US National Institute of Diabetes and Digestive and Kidney Diseases ) جمع آوری شده است. ما از ۵۳۲ نمونه استفاده کردیم. [ ۲] [ ۳]
در این مثال، ما ۳ برآورد چگالی برای "glu" ( با تمرکز بر روی گلوکز پلاسما ( به انگلیسی: plasma glucose ) ) انجام دادیم. یکی از آنها احتمال شرطی به شرط مبتلا بودن به دیابت، دومی به شرط مبتلا نبودن به دیابت و سومی بدون شرطی روی داشتن یا نداشتن دیابت است. سپس از برآوردهایی که برای احتمالات شرطی به دست آمد استفاده شد تا احتمال ابتلا به دیابت به شرط "glu" بدست بیاید.
داده های مربوط به "glu" از پکیچ MASS[ ۴] موجود در زبان برنامه نویسی آر بدست آمد. داده ها به طور کامل تر از طریق Pima. tr? و Pima. te? در زبان آر، قابل دسترسی است.
میانگین و انحراف معیار "glu" در کیس های مبتلا به دیابت به ترتیب برابر ۱۴۳٫۱ و ۳۱٫۲۶ است. در کیس های بدون دیابت، این مقادیر به ترتیب برابر ۱۱۰٫۰ و ۲۴٫۲۹ است. با توجه به این مقادیر، می توان دریافت که نمونه های مبتلا به دیابت دارای مقادیر بالاتری از "glu" هستند. این نکته با بررسی نمودارهای برآورد شده از توابع چگالی قابل فهم تر است.
شکل اول برآورد چگالی از احتمالات p ( glu | diabetes=۱ ) و p ( glu | diabetes=۰ ) و p ( glu ) را نشان می دهد. چگالی های برآورد شده، برآوردهای چگالی هسته هستند که با استفاده از هستهٔ گاوسی به دست آمده اند. به بیان دیگر، یک تابع چگالی گاوسی بر روی هر نقطه از داده قرار داده شده است، به طوری که مرکز تابع چگالی نقطه مدنظر باشد، سپس مجموع توابع چگالی روی گستره داده ها محاسبه شده است.





wiki: برآورد چگالی
