در علوم کامپیوتر، الگوریتم تقسیم و حل ( D& C ) ( به انگلیسی: Divide and conquer ) الگوی طراحی الگوریتم مهمی بر اساس بازگشت چند خطی است. یک الگوریتم تقسیم و حل از طریق تفکیک یک مسئله به دو یا چند زیرمسئله از یک نوع ( یا انواع وابسته به هم ) به صورت بازگشتی کار می کند. این تفکیک تا زمانی ادامه می یابد که زیرمسئله های حاصله به میزان کافی ساده شده باشند تا بتوان آن ها را مستقیماً حل کرد. جواب مسئلهٔ اصلی از ترکیب جواب های به دست آمده برای زیر مسئله ها به دست می آید.
این تکنیک مبنای الگوریتم های کارآمدی برای انواع مسئله ها است، به عنوان مثال، الگوریتم های مرتب سازی ( مثل مرتب سازی سریع و مرتب سازی ادغامی ) , ضرب اعداد بزرگ ( مثل کاراتسوبا ) , تجزیه کننده ( مثل تحلیلگر بالا به پایین ) ، و محاسبهٔ تبدیل فوریه گسسته ( تبدیل سریع فوریه ) از روش تقسیم و حل استفاده می کنند.
از سوی دیگر، توانایی درک و طراحیِ الگوریتم های حل و تقسیم هنری است که کسب مهارت در آن زمان زیادی می طلبد. به هنگام اثبات یک قضیه به کمک استقرا، غالباً نیازمند آنیم که به منظور دستیابی به یک روند بازگشتی، مسئلهٔ اصلی را با یک مسئلهٔ عمومی تر یا پیچیده تر جایگزین کنیم، و این در حالی است که روش منظمی برای یافتن تعمیم مناسب وجود ندارد.
گاهی نام «تقسیم و حل» در مورد الگوریتم هایی که هر مسئله را تنها به یک زیرمسئله تقلیل می دهند نیز به کار می رود، مانند الگوریتم جستجوی دودویی برای یافتن یک پرونده در یک لیست مرتب شده. [ ۱] با وجود این تعریف جامع، هر الگوریتمی که از بازگشت یا حلقه استفاده می کند، به نوعی می تواند «الگوریتم تقسیم و حل» تلقی شود. از این رو، بعضی از مؤلفان درعوض از نام «کاهش و حل» استفاده می کنند. [ ۲] این الگوریتم ها می توانند کارآمدتر از الگوریتم های تقسیم و حل معمولی، پیاده سازی شوند. به عنوان مثال، در صورت استفاده از رابطهٔ بازگشتی، این الگوریتم ها می توانند به حلقه های ساده تبدیل شوند.
معمولاً صحت یک الگوریتم تقسیم و حل به کمک استقرای ریاضی اثبات، و هزینهٔ محاسباتی آن نیز معمولاً از طریق حل روابط بازگشتی تعیین می شود.
الگوی تقسیم و حل اغلب برای یافتن راه حل بهینه از یک مسئله استفاده می شود. ایده اصلی این است که یک مسئلهٔ معین را به دو یا چند زیرمجموعه مشابه، اما ساده تر تقسیم کنیم تا به نوبه خود آنها را حل کند و راه حل های خود را برای حل مسئله مورد نظر تنظیم کند. مسئله های بسیار ساده به طور مستقیم حل می شود. به عنوان مثال، برای مرتب کردن یک لیست معین از اعداد طبیعی، آن را به دو لیست به طول n / 2 تقسیم می کنیم، هر یک را به نوبه خود مرتب می کنیم و هر دو نتیجه را به طور مناسب در هم ادغام می کنیم تا نسخه مرتب شده لیست به دست آید ( نگاه کنید به تصویر ) . در این مثال لیست های با طول یک نیاز به مرتب سازی ( حل ) ندارند. این روش به الگوریتم مرتب سازی ادغامی معروف است.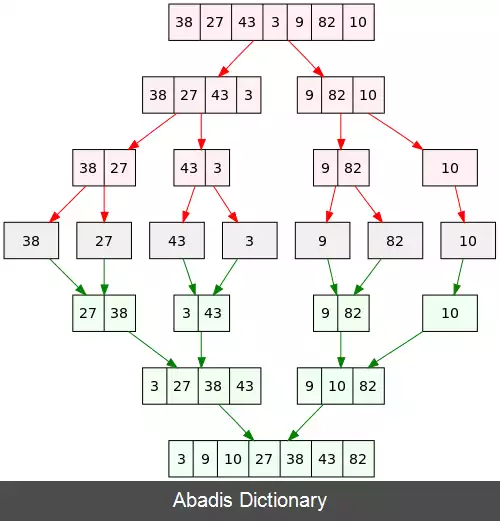
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین تکنیک مبنای الگوریتم های کارآمدی برای انواع مسئله ها است، به عنوان مثال، الگوریتم های مرتب سازی ( مثل مرتب سازی سریع و مرتب سازی ادغامی ) , ضرب اعداد بزرگ ( مثل کاراتسوبا ) , تجزیه کننده ( مثل تحلیلگر بالا به پایین ) ، و محاسبهٔ تبدیل فوریه گسسته ( تبدیل سریع فوریه ) از روش تقسیم و حل استفاده می کنند.
از سوی دیگر، توانایی درک و طراحیِ الگوریتم های حل و تقسیم هنری است که کسب مهارت در آن زمان زیادی می طلبد. به هنگام اثبات یک قضیه به کمک استقرا، غالباً نیازمند آنیم که به منظور دستیابی به یک روند بازگشتی، مسئلهٔ اصلی را با یک مسئلهٔ عمومی تر یا پیچیده تر جایگزین کنیم، و این در حالی است که روش منظمی برای یافتن تعمیم مناسب وجود ندارد.
گاهی نام «تقسیم و حل» در مورد الگوریتم هایی که هر مسئله را تنها به یک زیرمسئله تقلیل می دهند نیز به کار می رود، مانند الگوریتم جستجوی دودویی برای یافتن یک پرونده در یک لیست مرتب شده. [ ۱] با وجود این تعریف جامع، هر الگوریتمی که از بازگشت یا حلقه استفاده می کند، به نوعی می تواند «الگوریتم تقسیم و حل» تلقی شود. از این رو، بعضی از مؤلفان درعوض از نام «کاهش و حل» استفاده می کنند. [ ۲] این الگوریتم ها می توانند کارآمدتر از الگوریتم های تقسیم و حل معمولی، پیاده سازی شوند. به عنوان مثال، در صورت استفاده از رابطهٔ بازگشتی، این الگوریتم ها می توانند به حلقه های ساده تبدیل شوند.
معمولاً صحت یک الگوریتم تقسیم و حل به کمک استقرای ریاضی اثبات، و هزینهٔ محاسباتی آن نیز معمولاً از طریق حل روابط بازگشتی تعیین می شود.
الگوی تقسیم و حل اغلب برای یافتن راه حل بهینه از یک مسئله استفاده می شود. ایده اصلی این است که یک مسئلهٔ معین را به دو یا چند زیرمجموعه مشابه، اما ساده تر تقسیم کنیم تا به نوبه خود آنها را حل کند و راه حل های خود را برای حل مسئله مورد نظر تنظیم کند. مسئله های بسیار ساده به طور مستقیم حل می شود. به عنوان مثال، برای مرتب کردن یک لیست معین از اعداد طبیعی، آن را به دو لیست به طول n / 2 تقسیم می کنیم، هر یک را به نوبه خود مرتب می کنیم و هر دو نتیجه را به طور مناسب در هم ادغام می کنیم تا نسخه مرتب شده لیست به دست آید ( نگاه کنید به تصویر ) . در این مثال لیست های با طول یک نیاز به مرتب سازی ( حل ) ندارند. این روش به الگوریتم مرتب سازی ادغامی معروف است.

wiki: الگوریتم تقسیم و حل
