گروه متقارن آفین. گروه متقارن آفین شاخه ای از جبر در ریاضیات است که به مطالعه و توصیف تقارن های محور اعداد و کاشی کاری مثلثی منظم صفحه و اجسام با ابعاد بالاتر مرتبط می پردازد. علاوه بر این توصیف هندسی، گروه های متقارن وابسته به روش دیگری نیز تعریف می شوند. مثلا:به عنوان مجموعه ای از جایگشت های ( باز چینی ) اعداد صحیح که در زمان خاصی به صورت متناوب هستند یا به اصطلاح تخصصی تر، به عنوان گروه با مولد و روابط ( تعیین گروه با مولد و روابط بین آنها ) است که در ترکیبیات و نظریهٔ نمایش بررسی می شوند. یک گروه متقارن محدود، شامل همه جایگشت های یک مجموعه متناهی است. هر گروه متقارن وابسته، توسیع گروهی از یک گروه متقارن محدود است. بسیاری از ویژگی های ترکیبی مهم گروه های متقارن محدود می تواند به گروه های متقارن وابسته متناظر تعمیم داده شود. آمار جایشگت ( تصادفی ) مانند جایگشت و وراونگی را می توان در وابسته تعریف کرد. همان طور که در حالت محدود، تعاریف ترکیبی طبیعی برای این آمار نیز تفسیر هندسی دارند. گروه های متقارن وابسته روابط نزدیکی با سایر موضوعات ریاضی دارند، از جمله الگو ( ترفند ) های شعبده بازی و گروه های بازتابی پیچیده خاص است. بسیاری از ویژگی های ترکیبی و هندسی آنها به خانواده گسترده تر گروه های کاکسیتر تعمیم داده می شود.
گروه متقارن آفین را می توان توسط مولدها و روابط به عنوان گروهی مجرد، یا به طور معادل برحسب عبارات ملموس هندسی و مدل های ترکیبیاتی تعریف نمود. [ ۱]
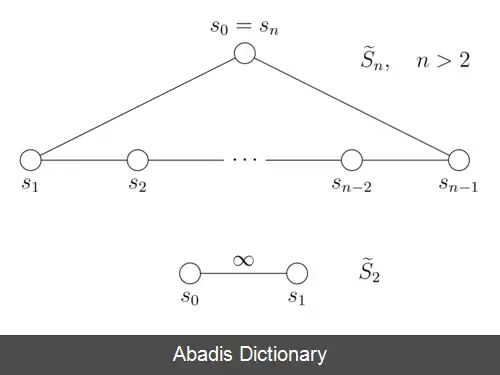
یکی از راه های تعریف گروه ها، استفاده از مولدها و روابط است. در این نوع تعریف، مولدها زیرمجموعه ای از عناصر گروه هستند که در صورت ترکیب، همه عناصر دیگر را تولید می کنند. روابط تعریف، سیستمی از معادلات هستند که مشخص می کنند چه زمانی ترکیب مولدها برابر هستند. [ الف] [ ۲] به این ترتیب گروه متقارن وابسته S ~ n _ام، توسط یک مجموعه درست می شود.
s 0 , s 1 , … , s n − 1
از n_مین عنصر از رابطه زیر پیروی می کند: اگر n ≥ 3 باشد
• s i 2 = 1 {\displaystyle s_{i}^{2}=1} ( که مولدها پیچشی هستند. )
• s i s j = s j s i {\displaystyle s_{i}s_{j}=s_{j}s_{i}} اگر j متعلق به j + 1 {\displaystyle j+1} و j − 1 {\displaystyle j - 1} نباشد، نشان می دهد برای این جفت ژنراتور خاصیت جابه جایی وجود دارد.
• s i s i + 1 s i = s i + 1 s i s i + 1 {\displaystyle s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}}
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگروه متقارن آفین را می توان توسط مولدها و روابط به عنوان گروهی مجرد، یا به طور معادل برحسب عبارات ملموس هندسی و مدل های ترکیبیاتی تعریف نمود. [ ۱]
یکی از راه های تعریف گروه ها، استفاده از مولدها و روابط است. در این نوع تعریف، مولدها زیرمجموعه ای از عناصر گروه هستند که در صورت ترکیب، همه عناصر دیگر را تولید می کنند. روابط تعریف، سیستمی از معادلات هستند که مشخص می کنند چه زمانی ترکیب مولدها برابر هستند. [ الف] [ ۲] به این ترتیب گروه متقارن وابسته S ~ n _ام، توسط یک مجموعه درست می شود.
s 0 , s 1 , … , s n − 1
از n_مین عنصر از رابطه زیر پیروی می کند: اگر n ≥ 3 باشد
• s i 2 = 1 {\displaystyle s_{i}^{2}=1} ( که مولدها پیچشی هستند. )
• s i s j = s j s i {\displaystyle s_{i}s_{j}=s_{j}s_{i}} اگر j متعلق به j + 1 {\displaystyle j+1} و j − 1 {\displaystyle j - 1} نباشد، نشان می دهد برای این جفت ژنراتور خاصیت جابه جایی وجود دارد.
• s i s i + 1 s i = s i + 1 s i s i + 1 {\displaystyle s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}}


wiki: گروه متقارن آفین
