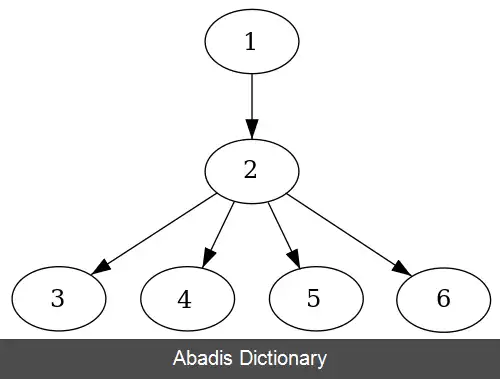
در گراف های جهت دار، زمانی می گوییم گره w بر گره v غلبه می کند که به ازای هر گره n همه مسیر ها از n به v ، از گره w عبور کند. در نتیجه می توان گفت هر گره بر خودش غلبه می کند. با توجه به تعریف می توان برای هر گره مجموعه ای از گره های سلطه گر در نظر گرفت که بر این گره غلبه می کنند. همچنین می توان برای هر گراف یک درخت سلطه گر تعریف کرد که به ازای هر گره در گراف، اجداد این گره در درخت، گره های سلطه گر بر این گره در گراف هستند.
• گره v {\displaystyle v} بر گره w {\displaystyle w} اکیداً غلبه می کند زمانی که گره v {\displaystyle v} بر گره w {\displaystyle w} غلبه کرده و v ≠ w {\displaystyle v\neq w} باشد.
• گره های سلطه گر آنی گره v {\displaystyle v} به مجموعه گره هایی می گویند که فقط بر گره v {\displaystyle v} به صورت اکید غلبه کرده و بر هیچ گره دیگری اکیداً غلبه نکند[ ۱] .
• گره های سلطه گر مرزی گره v {\displaystyle v} به مجموعه گره هایی می گویند که گره v {\displaystyle v} بر والدهای مستقیم آنها غلبه کرده ولی به صورت اکید بر آن گره ها غلبه نکند.
بنابر تعریف می توان برای سلطه گری اکید نتیجه گرفت که نزدیک گره سلطه گر اکید برای هر گره یکتا بوده و یک گره برای آن وجود دارد.
تعریف گره سلطه گر یا غالب برای اولین بار توسط ریس پروسر در مقاله ای تحت عنوان کاربردهای ماتریس بولی برای تحلیل نمودارهای جریان[ ۲] ارائه شد. او در این مقاله الگوریتمی برای پیدا کردن گره های سلطه گر ارائه نکرد و صرفاً آن را تعریف کرده. اولین الگوریتم برای این مساله ده سال بعد توسط ادوارد لوری و مدلاک ارائه شد[ ۳] . از کاربرد های آن می توان به زمینه های بهینه سازی برنامه، تولید کد، تست مدار اشاره کرد. همچنین در کامپایلر ها از اطلاعات حاصل از سلطه گری گره ها استفاده زیادی می شود. برای مثال یک کاربرد آن در کامپایلر برای پیدا کردن حلقه ها در بهینه سازی کد به کمک بلوک های پایه است[ ۴] .
با توجه به تعریف برای هر گره n اگر Dom ( n ) برابر با مجموعه گره های سلطه گر بر گره n در نظر بگیریم آنگاه رابطه زیر را خواهیم داشت.
Dom ( n ) = ( ⋂ p ∈ p r e d s ( n ) Dom ( p ) ) ∪ { n } در اینجا p r e d s ( n ) برابر است با مجموعه تمام گره هایی که وارد گره n می شوند یعنی یک یال از سمت آنها به n وجود دارد. همچنین برای گره شروع در گراف داریم Dom ( n 0 ) = { n 0 } با داشتن این اطلاعات برای پیدا کردن گره های سلطه گر هر گره در گراف می توان الگوریتم زیر را پیاده سازی کرد.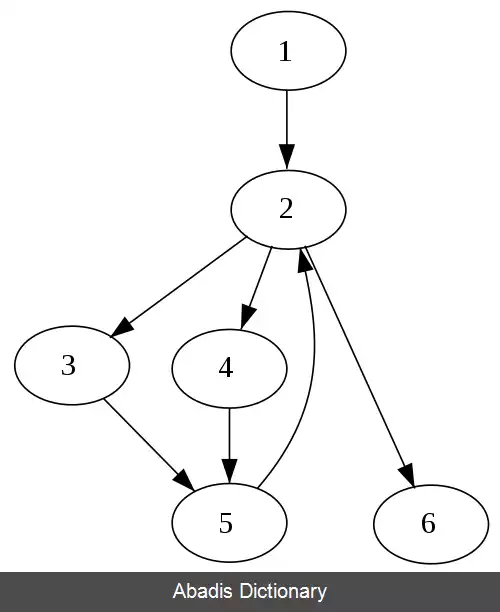
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• گره v {\displaystyle v} بر گره w {\displaystyle w} اکیداً غلبه می کند زمانی که گره v {\displaystyle v} بر گره w {\displaystyle w} غلبه کرده و v ≠ w {\displaystyle v\neq w} باشد.
• گره های سلطه گر آنی گره v {\displaystyle v} به مجموعه گره هایی می گویند که فقط بر گره v {\displaystyle v} به صورت اکید غلبه کرده و بر هیچ گره دیگری اکیداً غلبه نکند[ ۱] .
• گره های سلطه گر مرزی گره v {\displaystyle v} به مجموعه گره هایی می گویند که گره v {\displaystyle v} بر والدهای مستقیم آنها غلبه کرده ولی به صورت اکید بر آن گره ها غلبه نکند.
بنابر تعریف می توان برای سلطه گری اکید نتیجه گرفت که نزدیک گره سلطه گر اکید برای هر گره یکتا بوده و یک گره برای آن وجود دارد.
تعریف گره سلطه گر یا غالب برای اولین بار توسط ریس پروسر در مقاله ای تحت عنوان کاربردهای ماتریس بولی برای تحلیل نمودارهای جریان[ ۲] ارائه شد. او در این مقاله الگوریتمی برای پیدا کردن گره های سلطه گر ارائه نکرد و صرفاً آن را تعریف کرده. اولین الگوریتم برای این مساله ده سال بعد توسط ادوارد لوری و مدلاک ارائه شد[ ۳] . از کاربرد های آن می توان به زمینه های بهینه سازی برنامه، تولید کد، تست مدار اشاره کرد. همچنین در کامپایلر ها از اطلاعات حاصل از سلطه گری گره ها استفاده زیادی می شود. برای مثال یک کاربرد آن در کامپایلر برای پیدا کردن حلقه ها در بهینه سازی کد به کمک بلوک های پایه است[ ۴] .
با توجه به تعریف برای هر گره n اگر Dom ( n ) برابر با مجموعه گره های سلطه گر بر گره n در نظر بگیریم آنگاه رابطه زیر را خواهیم داشت.
Dom ( n ) = ( ⋂ p ∈ p r e d s ( n ) Dom ( p ) ) ∪ { n } در اینجا p r e d s ( n ) برابر است با مجموعه تمام گره هایی که وارد گره n می شوند یعنی یک یال از سمت آنها به n وجود دارد. همچنین برای گره شروع در گراف داریم Dom ( n 0 ) = { n 0 } با داشتن این اطلاعات برای پیدا کردن گره های سلطه گر هر گره در گراف می توان الگوریتم زیر را پیاده سازی کرد.


wiki: گره سلطه گر
