گراف های کامل دوبخشی ( Complete bipartite graphs ) به گراف های کاملی گفته می شود که در آن ها مجموعهٔ رأس ها را بتوان به دو زیرمجموعهٔ V 1 و V 2 افراز کرد، به گونه ای که هر راس از مجموعه V 1 به تمام رئوس مجموعه V 2 متصل باشد. [ ۱] [ ۲] اگر | V 1 | = n و | V 2 | = m باشد، گراف کامل دوبخشیی که از این دو مجموعه رئوس ساخته میشود را معمولاً با K n , m نمایش می دهند. آغاز نظریه گراف ها معمولاً با کار اویلر بر روی هفت پلِ کونیکسبرگ در سال ۱۷۳۶ گره خورده است. [ ۳] با این حال، تاریخچه گرافهای کامل دوبخشی به رسم های رامون یوی در سال ۱۶۶۹ بازمی گردد. [ ۴] [ ۵]
• پیدا کردن جواب این سؤال که آیا یک گراف دوبخشی یک زیرگراف کامل دو بخشی به فرمِ K i , i {\displaystyle K_{i, i}} دارد ان پی کامل است. [ ۶]
• هر گراف کامل دو بخشی K n , n {\displaystyle K_{n, n}} یک گراف مور و یک cage از نوع ( n , 4 ) {\displaystyle ( n, 4 ) } است. [ ۷]
• هر گراف کامل دوبخشی K n , m {\displaystyle K_{n, m}} به تعداد n m − 1 m n − 1 {\displaystyle n^{m - 1}m^{n - 1}} درخت پوشا دارد. [ ۸]
• K 1 , n {\displaystyle K_{1, n}} به ازای هر n {\displaystyle n} دلخواه هم یک ستاره هم یک درخت است. [ ۲]
• K 1 , 3 {\displaystyle K_{1, 3}} در اصطلاح نظریه گراف ها پنجه نام دارد و برای ساخت گرافهای پنجه آزاد بکار بگرفته می شود. [ ۹]
گراف پایین ۵ راس دارد، دو راس آن به یکدیگر متصل نیستند ولی به تمام سه راس دیگر متصلند، همچنین سه راس گراف به یکدیگر متصل نیستند ولی به دو راس دیگر متصلند. این گراف در نظریه گراف ها با K 2 , 3 نمایش داده می شود.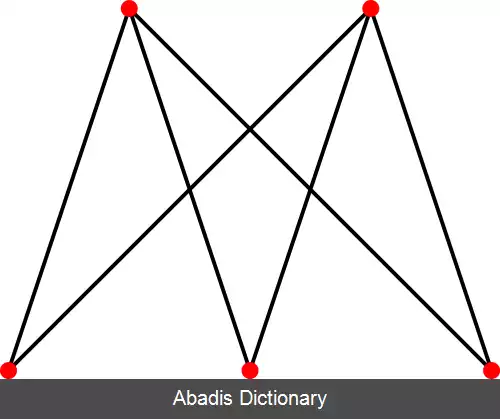
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• پیدا کردن جواب این سؤال که آیا یک گراف دوبخشی یک زیرگراف کامل دو بخشی به فرمِ K i , i {\displaystyle K_{i, i}} دارد ان پی کامل است. [ ۶]
• هر گراف کامل دو بخشی K n , n {\displaystyle K_{n, n}} یک گراف مور و یک cage از نوع ( n , 4 ) {\displaystyle ( n, 4 ) } است. [ ۷]
• هر گراف کامل دوبخشی K n , m {\displaystyle K_{n, m}} به تعداد n m − 1 m n − 1 {\displaystyle n^{m - 1}m^{n - 1}} درخت پوشا دارد. [ ۸]
• K 1 , n {\displaystyle K_{1, n}} به ازای هر n {\displaystyle n} دلخواه هم یک ستاره هم یک درخت است. [ ۲]
• K 1 , 3 {\displaystyle K_{1, 3}} در اصطلاح نظریه گراف ها پنجه نام دارد و برای ساخت گرافهای پنجه آزاد بکار بگرفته می شود. [ ۹]
گراف پایین ۵ راس دارد، دو راس آن به یکدیگر متصل نیستند ولی به تمام سه راس دیگر متصلند، همچنین سه راس گراف به یکدیگر متصل نیستند ولی به دو راس دیگر متصلند. این گراف در نظریه گراف ها با K 2 , 3 نمایش داده می شود.

wiki: گراف کامل دوبخشی
