در هندسهٔ محاسباتی و ناوبری روبات ها، گراف پدیداری ( به انگلیسی: Visibility Graph ) گرافی است شامل نقاطی که از ناحیهٔ منطقهٔ مورد نظر قابل دید است. در واقع هر گره نمایش دهندهٔ مکانی در محیط است و لبهٔ گراف بین دو نقطهٔ مورد نظر، نشان دهندهٔ ارتباط بین آن دو نقطه، یا دیده شدن یکی از نقاط با قرار گرفتن در نقطهٔ دیگر است و هیج مانعی سد راه دیده شدن این دو نقطه از همدیگر نمی شود.
با استفاده از گراف های پدیداری می توان کمینه فاصله اقلیدسی بین دو نقطهٔ مورد نظر در فضایی شامل موانع چند ضلعی را پیدا کرد. همیشه کمترین فاصله بین دو نقطه خط راست بین آن دو نقطه هست، مگر آنکه مانعی در میان مسیر مورد نظر باشد. در اینصورت گوشهٔ چند ضلعی مورد نظر باید به عنوان یکی از نقاط میانی ( راس های گراف پدیداری ) انتخاب کرد. به اینصورت می توان مسئلهٔ مسیر بهینه در فضای اقلیدسی را به مسئلهٔ کوتاه ترین مسیر در یک گراف تبدیل کرد. اکنون در اینجا می توان مسئله را به قسمت تقسیم کرد: ( ۱ ) ساختن گراف پدیداری از روی مسئلهٔ کوتاه ترین مسیر در فضای اقلیدسی ( ۲ ) حل مسئلهٔ کوتاه ترین مسیر مانند الگوریتم دایکسترا در یک گراف. برای مسیر یابی روباتی که دارای اندازه ای قابل توجه است، می توان مسئله را تعمیم داد. در واقع در این حالت مسیر بهینه نمی تواند کاملاً در لبهٔ موانع عبور کند. چون اگر اینطور باشد، روبات با شعاع غیر جزئی با موانع برخورد می کند. مسئله را می توان به اینصورت حل کرد که موانع را کمی بزرگتر از آنچه هستند در نظر گرفت و سپس مراحل فوق را در این حالت انجام داد. یکی دیگر از کاربردهای گراف پدیداری در بدست آوردن مکان بهینه برای قرار دادن آنتن های رادیویی است.
گراف پدیداری یک چندضلعی ساده، گرافی شامل گوشه های آن، به عنوان گره های آن است. گراف پدیداری چند ضلعی های ساده، یک گراف همیلتونی است. چون مرز یک چند ضلعی تشکیل یک دور همیلتونی می دهد. این نوع تعریف گراف پدیداری کامل دقیق نیست، بدین مفهوم که هنوز الگوریتمی وجود ندارد که بتواند در زمان چند جمله ای از روی یک گراف پدیداری، چند ضلعی ( های ) متناظر با آن را در صورت وجود بازسازی کند.
در مسئلهٔ نگارخانه هنری ( هندسه ) هدف پیدا کردن مجموعه از نقاط در محیط است، بطوریکه بتوان تمام نقاط در محیط را از روی آن نقاط به طور کامل مشاهده کرد. برخی از حالت های مسئلهٔ نگارخانه هنری را می توان به صورتی معادل از طریق پیدا کردن زیر مجموعهٔ غالب در یک گراف حل کرد. خطوط bitanget مجموعه ای از اشکال عبارت است از کلیهٔ خطوطی که حداقل بر دو نقطه از شکل مماس باشند. مجموعهٔ bitangetهای یک مجموعه چند ضلعی، یک گراف پدیداری تشکیل می دهند که راس های آن شامل گوشه های چندضلعی ها هستند و داخل چند ضلعی ها به عنوان موانع محیط محسوب می شوند. یکی از ایده ها برای بهینه تر کردن عملکرد گراف های پدیداری استفاده از bianget در ساختن آنهاست.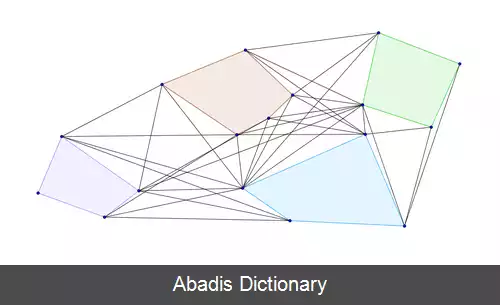
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبا استفاده از گراف های پدیداری می توان کمینه فاصله اقلیدسی بین دو نقطهٔ مورد نظر در فضایی شامل موانع چند ضلعی را پیدا کرد. همیشه کمترین فاصله بین دو نقطه خط راست بین آن دو نقطه هست، مگر آنکه مانعی در میان مسیر مورد نظر باشد. در اینصورت گوشهٔ چند ضلعی مورد نظر باید به عنوان یکی از نقاط میانی ( راس های گراف پدیداری ) انتخاب کرد. به اینصورت می توان مسئلهٔ مسیر بهینه در فضای اقلیدسی را به مسئلهٔ کوتاه ترین مسیر در یک گراف تبدیل کرد. اکنون در اینجا می توان مسئله را به قسمت تقسیم کرد: ( ۱ ) ساختن گراف پدیداری از روی مسئلهٔ کوتاه ترین مسیر در فضای اقلیدسی ( ۲ ) حل مسئلهٔ کوتاه ترین مسیر مانند الگوریتم دایکسترا در یک گراف. برای مسیر یابی روباتی که دارای اندازه ای قابل توجه است، می توان مسئله را تعمیم داد. در واقع در این حالت مسیر بهینه نمی تواند کاملاً در لبهٔ موانع عبور کند. چون اگر اینطور باشد، روبات با شعاع غیر جزئی با موانع برخورد می کند. مسئله را می توان به اینصورت حل کرد که موانع را کمی بزرگتر از آنچه هستند در نظر گرفت و سپس مراحل فوق را در این حالت انجام داد. یکی دیگر از کاربردهای گراف پدیداری در بدست آوردن مکان بهینه برای قرار دادن آنتن های رادیویی است.
گراف پدیداری یک چندضلعی ساده، گرافی شامل گوشه های آن، به عنوان گره های آن است. گراف پدیداری چند ضلعی های ساده، یک گراف همیلتونی است. چون مرز یک چند ضلعی تشکیل یک دور همیلتونی می دهد. این نوع تعریف گراف پدیداری کامل دقیق نیست، بدین مفهوم که هنوز الگوریتمی وجود ندارد که بتواند در زمان چند جمله ای از روی یک گراف پدیداری، چند ضلعی ( های ) متناظر با آن را در صورت وجود بازسازی کند.
در مسئلهٔ نگارخانه هنری ( هندسه ) هدف پیدا کردن مجموعه از نقاط در محیط است، بطوریکه بتوان تمام نقاط در محیط را از روی آن نقاط به طور کامل مشاهده کرد. برخی از حالت های مسئلهٔ نگارخانه هنری را می توان به صورتی معادل از طریق پیدا کردن زیر مجموعهٔ غالب در یک گراف حل کرد. خطوط bitanget مجموعه ای از اشکال عبارت است از کلیهٔ خطوطی که حداقل بر دو نقطه از شکل مماس باشند. مجموعهٔ bitangetهای یک مجموعه چند ضلعی، یک گراف پدیداری تشکیل می دهند که راس های آن شامل گوشه های چندضلعی ها هستند و داخل چند ضلعی ها به عنوان موانع محیط محسوب می شوند. یکی از ایده ها برای بهینه تر کردن عملکرد گراف های پدیداری استفاده از bianget در ساختن آنهاست.

wiki: گراف پدیداری
