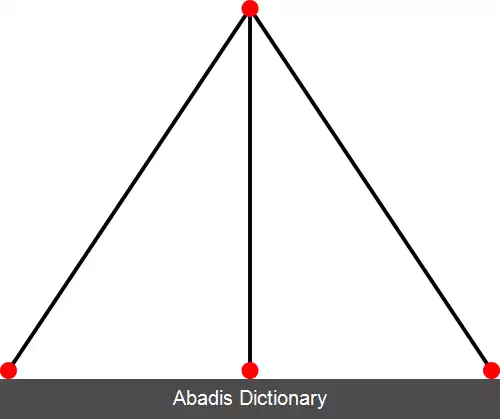
گراف های پنجه آزاد. در نظریه گراف، که بخشی از ریاضیات است، گراف پنجه آزاد گرافی است که زیرگراف پنجه نداشته باشد. پنجه نام دیگر گراف دوبخشی کامل K 1 , 3 است ( یک گراف ستاره با سه برگ و یک راس مرکزی ) . یک گراف پنجه آزاد گرافی است که هیچ یک از زیر گراف های آن پنجه نباشد؛ یعنی هر زیرگراف چهار راسی آن یالی بیش از سه یالی که آن ها را بدین شکل به هم متصل می کنند داشته باشد. به بیانی دیگر گراف پنجه آزاد گرافی است که در آن مکمل گراف القایی همسایه های هر راس آن گراف، مثلث آزاد باشد. [ ۱]
گراف های پنجه آزاد، در ابتدا به عنوان تعمیم گراف یالی شناخته می شدند، اما با کشف این سه خاصیت مهم، اهمیت بیشتری پیدا کردند:
• اثبات این که هر گراف پنجه آزاد زوج راسی تطابق کامل دارد.
• کشف راه حل چند جمله ای برای پیدا کردن مجموعه مستقل بیشینه در گراف های پنجه آزاد.
• توصیف خصوصیات گراف ایده آل[ ۱] پنجه آزاد.
• گراف یالی L ( G ) {\displaystyle L ( G ) } هر گراف G {\displaystyle G} پنجه آزاد است؛ L ( G ) {\displaystyle L ( G ) } به ازای هر یال G {\displaystyle G} یک راس دارد، و دو راس در L ( G ) {\displaystyle L ( G ) } با یکدیگر مجاورند هرگاه یال های متناظر آن ها در G {\displaystyle G} ، در یک سر خود مشترک باشند. گراف یالی L ( G ) {\displaystyle L ( G ) } نمی تواند پنجه داشته باشد، زیرا اگر سه یال e 1 , e 2 {\displaystyle e_{1}, e_{2}} و e 3 {\displaystyle e_{3}} هر سه در G {\displaystyle G} با یال دیگری مثل e 4 {\displaystyle e_{4}} سر مشترک داشته باشند، طبق اصل لانه کبوتر حداقل دوتا از یال ها در یک سر مشترک e 4 {\displaystyle e_{4}} با آن اشتراک دارند و بنابراین با هم مشترک هستند و در L ( G ) {\displaystyle L ( G ) } بین آنها یال وجود دارد.
• گراف دی براین ( گرافی که به هر راس آن یک کد n {\displaystyle n} بیتی باینری نسبت داده شده است و بین دو راسی که n − 1 {\displaystyle n - 1} هم پوشانی دارند یال وجود دارد ) پنجه آزاد است.
• مُکمّل هر گراف مثلث - آزاد پنجه آزاد است. [ ۲]
• گراف اِشلفلی که ۲۷ راس دارد یک گراف پنجه آزاد است. [ ۳]
بررسی کردن پنجه آزاد بودن یا نبودن یک گراف دلخواه با n رأس و m یال در زمان O ( n 4 ) کار ساده ای است، کافی است به ازای هر ۴ رأس بررسی کرد که آیا زیرگراف القایی روی آن ۴ رأس تشکیل یک پنجه می دهد یا خیر. [ ۴] رویکردی پیچیده تر اما اندکی کارا تر این است که در گراف پنجه آزاد، گراف مکمل همسایه های هر رأس مثلث آزاد نباشد. یک گراف مثلث دارد اگر و تنها اگر عددی ناصفر روی قطر مربع ماتریس مجاورت آن باشد، پس یافتن مثلث در گراف از نظر پیچیدگی زمانی مانند محاسبهٔ ضرب دو ماتریس n × n است. از این رو، با استفاده از الگوریتم کوپراسمیت–وینوگارد زمان تشخیص پنجه آزاد بودن یک گراف O ( n 3. 376 ) خواهد بود. [ ۵]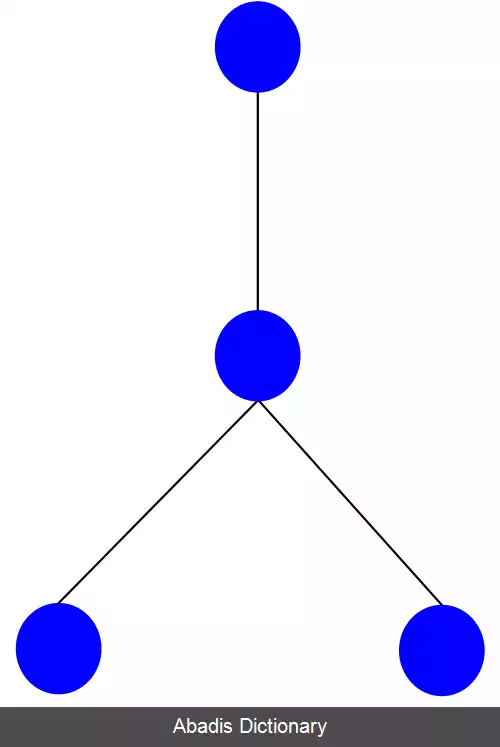
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگراف های پنجه آزاد، در ابتدا به عنوان تعمیم گراف یالی شناخته می شدند، اما با کشف این سه خاصیت مهم، اهمیت بیشتری پیدا کردند:
• اثبات این که هر گراف پنجه آزاد زوج راسی تطابق کامل دارد.
• کشف راه حل چند جمله ای برای پیدا کردن مجموعه مستقل بیشینه در گراف های پنجه آزاد.
• توصیف خصوصیات گراف ایده آل[ ۱] پنجه آزاد.
• گراف یالی L ( G ) {\displaystyle L ( G ) } هر گراف G {\displaystyle G} پنجه آزاد است؛ L ( G ) {\displaystyle L ( G ) } به ازای هر یال G {\displaystyle G} یک راس دارد، و دو راس در L ( G ) {\displaystyle L ( G ) } با یکدیگر مجاورند هرگاه یال های متناظر آن ها در G {\displaystyle G} ، در یک سر خود مشترک باشند. گراف یالی L ( G ) {\displaystyle L ( G ) } نمی تواند پنجه داشته باشد، زیرا اگر سه یال e 1 , e 2 {\displaystyle e_{1}, e_{2}} و e 3 {\displaystyle e_{3}} هر سه در G {\displaystyle G} با یال دیگری مثل e 4 {\displaystyle e_{4}} سر مشترک داشته باشند، طبق اصل لانه کبوتر حداقل دوتا از یال ها در یک سر مشترک e 4 {\displaystyle e_{4}} با آن اشتراک دارند و بنابراین با هم مشترک هستند و در L ( G ) {\displaystyle L ( G ) } بین آنها یال وجود دارد.
• گراف دی براین ( گرافی که به هر راس آن یک کد n {\displaystyle n} بیتی باینری نسبت داده شده است و بین دو راسی که n − 1 {\displaystyle n - 1} هم پوشانی دارند یال وجود دارد ) پنجه آزاد است.
• مُکمّل هر گراف مثلث - آزاد پنجه آزاد است. [ ۲]
• گراف اِشلفلی که ۲۷ راس دارد یک گراف پنجه آزاد است. [ ۳]
بررسی کردن پنجه آزاد بودن یا نبودن یک گراف دلخواه با n رأس و m یال در زمان O ( n 4 ) کار ساده ای است، کافی است به ازای هر ۴ رأس بررسی کرد که آیا زیرگراف القایی روی آن ۴ رأس تشکیل یک پنجه می دهد یا خیر. [ ۴] رویکردی پیچیده تر اما اندکی کارا تر این است که در گراف پنجه آزاد، گراف مکمل همسایه های هر رأس مثلث آزاد نباشد. یک گراف مثلث دارد اگر و تنها اگر عددی ناصفر روی قطر مربع ماتریس مجاورت آن باشد، پس یافتن مثلث در گراف از نظر پیچیدگی زمانی مانند محاسبهٔ ضرب دو ماتریس n × n است. از این رو، با استفاده از الگوریتم کوپراسمیت–وینوگارد زمان تشخیص پنجه آزاد بودن یک گراف O ( n 3. 376 ) خواهد بود. [ ۵]


wiki: گراف های پنجه آزاد
